С другой стороны двойное векторное произведение можно преобразовать следующим образом:
Подставляя полученные выражения в исходное равенство получим:
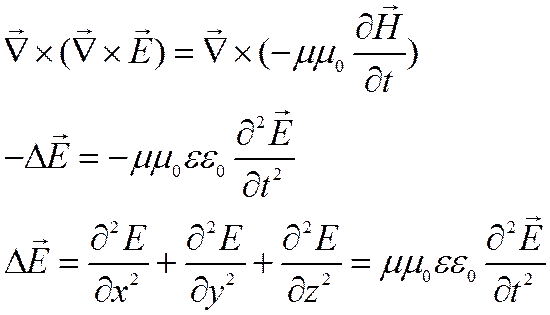
Сравнивая полученное нами уравнение с волновым уравнением:
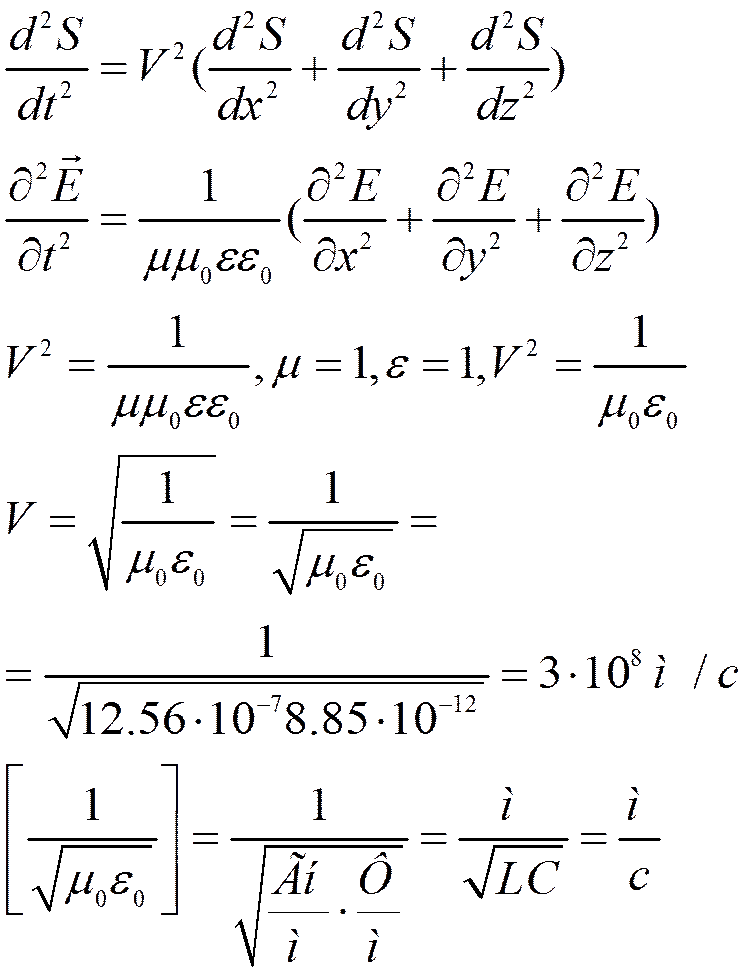
Видим, что из уравнений Максвелла, мы получили, что вектор напряжённости электростатического поля удовлетворяет волновому уравнению, т. е. из уравнения Максвелла следует уравнение электромагнитной волны. Решением этого дифференциального уравнения является функция:
E = E0Cos( w t – kx);
Если среда вакуум, то:
= 
ф/м, 
Гн/м.
Физический смысл системы уравнений Максвелла состоит в следующем: источниками электромагнитного поля являются плотность электрического заряда r и плотность тока 
, кроме того, даже в отсутствие плотности электрического заряда и плотности тока источником электрического поля является быстрота изменения во времени магнитного поля и наоборот, источником магнитного поля является быстрота изменения во времени электрического поля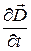 
. Сказанное дополняет выявление физического смысла каждого уравнения системы уравнений Максвелла в отдельности. Так уравнение (1) является математическим следствием физического условия отсутствия в природе магнитных зарядов, уравнение (3) описывает связь электрического поля с объемной плотностью электрического заряда, уравнение (2) описывает явление электромагнитной индукции, открытое М.Фарадеем, уравнение (4) – «закон полного тока».- является отражением того факта, что формирование магнитного поля в равной степени обусловлено и плотностью тока проводимости и плотностью тока смещения: 
.
Выпишем рядом дифференциальную и интегральную формы системы уравнений Максвелла:
Интересно сравнить между собой дифференциальную и интегральную формы системы уравнений Максвелла. В математическом плане различие этих форм состоит, в первую очередь, в том, что первая форма требует существования первых пространственных частных производных, входящих в определение дивергенции и ротора векторного поля, вторая форма не содержит пространственных производных и допускает возможность разрывных, недифференцируемых полей. Говорят, что интегральная форма системы уравнений Максвелла содержательнее дифференциальной, хотя в пределах физической применимости обе системы уравнений равнозначны, поскольку все скачки полей в макроэлектродинамике должны рассматриваться как пределы микромасштабных плавных переходов, так чтобы имелась возможность осреднения микровеличин. Если учесть сказанное, то резкие скачки полей, в частности связанные с точечными электрическими зарядами, можно рассматривать и в дифференциальной формулировке с помощью аппарата обобщённых функций. Так, например, точечный заряд q в точке пространства, описываемой радиусом вектором 
, можно представить в форме:
,
где 
, 
- дельта-функция Дирака, описанная в Приложении. Правомерность такого представления основана на интегральном следствии из него:
.
Интегральная форма системы уравнений Максвелла доставляет удобный математический аппарат решения прикладных задач электродинамики при условии достаточно высокой степени симметрии или при заданных законах распределения искомых векторных полей. Заметим, что в этих условиях и использование дифференциальной формы системы уравнений Максвелла достаточно эффективно.
Вместе с тем, система уравнений Максвелла в интегральной формулировке затушёвывает принцип локального взаимодействия, локальной связи электрического и магнитного полей, принцип близкодействия, лежащий в основе современных физических представлений.
