Задача 1. Найти общий интеграл дифференциального уравнения:
1. 6x dx - 6y dy = 2x2 ydy – 3xy2 dx
2. (ex + 8) dy – yex dx = 0
3. 
4. 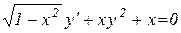
5. x dx – y dy = x2 y dy – xy2 dx
6. 
7. 
8. 6x dx - 6y dy = 3x2 y dy – 2xy2 dx
9. (1 + ex) y¢ = yex
10. 
11. 
12. 2x dx – y dy = x2 y dy – xy2 dx
13. 
14. 
15. 2x dx –2 y dy = x2 y dy – 2xy2 dx
16. y lny + xy’ = 0
17. (3 + ex) yy¢ = ex
18. (x2 – 1) yy¢ + 2xy2 = 0
19. 
20. 
21. 
22. 6x dx - y dy = x2 y dy – 3xy2 dx
23. y (1+lny) + xy’ = 0
24. (1 + ex) yy¢ = ex
25. 4x dx - 3y dy = 3x2 y dy – 2 xy2 dx
26. 
27. x2 yy¢ + y2 = 2
28. 
29. 20 x dx - 3y dy = 3x2 y dy – 5 xy2 dx
30. 
Задача 2. Найти общий интеграл дифференциального уравнения:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 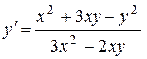
11.  12.
12. 
13. 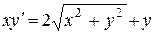 14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 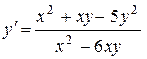
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
Задача 3. Найти общий интеграл дифференциального уравнения:
1.  2.
2. 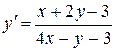
3. 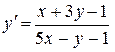 4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 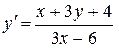
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 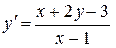
23.  24.
24. 
25.  26.
26. 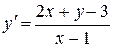
27.  28.
28. 
29. 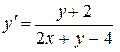 30.
30. 
Задача 4. Решить задачу Коши:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 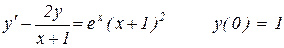
13. 
14. 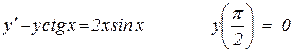
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 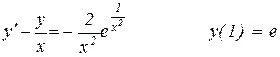
24. 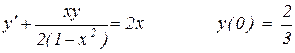
25. 
26. 
27. 
28. 
29. 
30. 
Задача 5. Найти решение задачи Коши:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 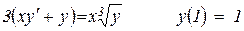
10. 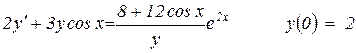
11. 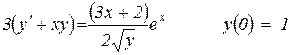
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задача 6. Проинтегрировать уравнение:
1. 3x2 еy dx + (x3 ey -1) dy = 0
2. 
3. (3x2 +4y2)dx + (8xy + ey) dy = 0
4. 
5. (y2 +ysec2 x) dx + (2xy +tg x) dy = 0
6. (3x2 y+2y+3) dx + (x3 +2x +3y2) dy = 0
7. 
8. (sin2x - 2cos(x+y)) dx - 2cos(x+y) dy = 0
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. ey dx + (cos y+x ey)dy = 0
20. (y3 +cos x)dx + (3xy2 + ey) dy = 0
21. 
22. (5xy2 -x3) dx + (5x2 y - y) dy = 0
23. (cos(x+y2) + sinx) dx + 2y cos(x+y2) dy = 0
24. (x2 - 4xy - 2y2) dx + (y2 -4xy -2x2) dy = 0
25. 
26. 
27. 
28. 2 (3xy2 + 2x3) dx + 3(2x2 y + y2) dy = 0
29. 
30. 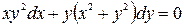
Задача 7.
1. Найти линию, проходящую через точку М0 (3;5) и обладающей тем свойством, что в любой точке М нормальный вектор MN с концами на оси OY имеет длину 5 ед. и образует острый угол с положительным направлением оси OY
2. Найти линию, проходящую через М0 (1;1), если отрезок любой её нормали, заключённый между осями координат, делится точкой линии в отношении 1:2 (считая от оси ординат)
3. Найти линию, проходящую через М0 (2;1), если отрезок любой её касательной между точкой касания и осью ординат, делится в точке пересечения с осью абсцисс в отношении 1:2 (считая от оси ординат)
4. Найти линию, проходящую через М0 (2;1), если отрезок любой её касательной, заключённой между осями координат, делится в точке касания в отношении 1:2 (считая от оси ординат)
5. Найти линию, проходящую через М0 (1;е), и обладающую тем свойством, что в любой её точке М касательный вектор MN с концом на оси ОХ имеет проекцию на ось ОХ, обратно пропорциональную абсциссе точки М с коэффициентом пропорциональности  .
.
6. Найти линию, проходящую через М0 (1;2), и обладающую тем свойством, что в любой её точке М касательный вектор MN с концом на оси ОY имеет проекцию на ось ОY, равную –1.
7. Найти кривую, для которой площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 9.
8. Найти кривую, для которой сумма катетов треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 5.
9. Найти кривую, обладающую следующим свойством: отрезок оси абсцисс, отсекаемый касательной и нормалью, проведёнными из произвольной точки кривой, равен 2.
10. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.
11. Найти кривые, обладающие следующим свойством: если через любую точку кривой провести прямые, параллельные осям координат, до встречи с этими осями, то площадь полученного прямоугольника делится кривой в отношении 1:2
12. Найти кривую, у которой точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат.
13. Найти кривую, у которой расстояние любой касательной от начала координат равно абсциссе точки касания.
14. Найти кривые, у которых площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, есть величина постоянная, равная 12.
15. Найти кривые, у которых площадь треугольника, ограниченного осью абсцисс, касательной и отрезком от начала координат до точки касания, есть величина постоянная, равная 4.
16. Найти линию, проходящую через точку М0 (9;3) и обладающей тем свойством, что в любой точке М нормальный вектор MN с концом на оси OY имеет длину 15 ед. и образует острый угол с положительным направлением оси OY
17. Найти линию, проходящую через М0 (0;1), если отрезок любой её нормали, заключённый между осями координат, делится точкой линии в отношении 2:3 (считая от оси ординат)
18. Найти линию, проходящую через М0 (2;1), если отрезок любой её касательной между точкой касания и осью ординат, делится в точке пересечения с осью абсцисс в отношении 1:2 (считая от оси ординат)
19. Найти линию, проходящую через М0 (1;3), если отрезок любой её касательной, заключённой между осями координат, делится в точке касания в отношении 2:1 (считая от оси ординат)
20. Найти линию, проходящую через М0 (1;1/е), и обладающую тем свойством, что в любой её точке М касательный вектор MN с концом на оси ОХ имеет проекцию на ось ОХ, обратно пропорциональную абсциссе точки М с коэффициентом пропорциональности k = 2.
21. Найти линию, проходящую через М0 (1;4), и обладающую тем свойством, что в любой её точке М касательный вектор MN с концом на оси ОY имеет проекцию на ось ОY, равную 2.
22. Найти кривую, для которой площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 4.
23. Найти кривую, для которой сумма катетов треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 7.
24. Найти кривую, обладающую следующим свойством: отрезок оси абсцисс, отсекаемый касательной и нормалью, проведёнными из произвольной точки кривой, равен 6.
25. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, втрое меньшую абсциссы точки касания.
26. Найти кривые, обладающие следующим свойством: если через любую точку кривой провести прямые, параллельные осям координат, до встречи с этими осями, то площадь полученного прямоугольника делится кривой пополам.
27. Кривая проходит через точку (2;4), и обладает тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведённой в любой точке кривой равен кубу абсциссы точки касания. Найти уравнение кривой.
28. Найти уравнение кривой, проходящей через точку (1;5),и обладающей следующим свойством: отрезок, отсекаемый на оси ординат любой касательной, равен утроенной абсциссе точки касания.
29. Кривая проходит через точку (1;2), и обладает тем свойством, что произведение углового коэффициента касательной в любой её на сумму координат точки касания равно удвоенной ординате этой точки. Найти уравнение кривой.
30. Найти кривые, у которых площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, есть величина постоянная, равная 10.
Задача 8. Найти общее решение уравнения:
1.  2.
2. 
3. 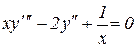 4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 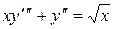
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23. 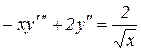 24.
24. 
25.  26.
26. 
27.  28.
28. 
29. 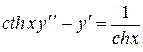 30.
30. 
Примечание: ò sh x dx = ch x + C
ò ch x dx = sh x + C
ò th x dx = ln(ch x) + C
ò cth x dx = ln | sh x| + C
Задача 9. Решить задачу Коши:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задача 10. Найти общее решение дифференциального уравнения:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 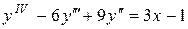
19.  20.
20. 
21. 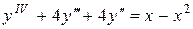 22.
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 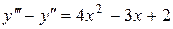
29.  30.
30. 
Задача 11. Найти общее решение дифференциального уравнения:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 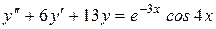
9. 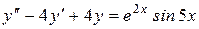 10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 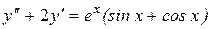
21. 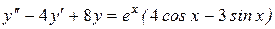 22.
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
Задача 12. Найти общее решение дифференциального уравнения:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 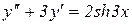
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задача 13. Найти общее решение уравнения:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 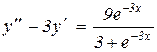
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 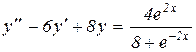
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
Задача 14. Решить системы уравнений ( означает
означает  и т.д., для облегчения работы в некоторых вариантах указаны корни характеристического уравнения)
и т.д., для облегчения работы в некоторых вариантах указаны корни характеристического уравнения)
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 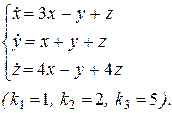
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 






