Преобразования Галилея:
Рассмотрим две системы:
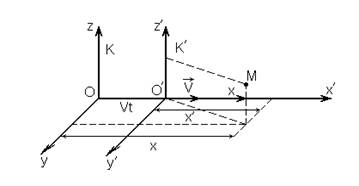Пусть 
движется со скоростью 
вдоль оси x. Справедливы следующие преобразования:
(время течет одинаково)
Экспериментально установлено, что если движется равномерно и прямолинейно относительно K, то физические законы одинаковы в двух системах или инвариантны относительно преобразований Галилея.
Т. е. равномерное и прямолинейное движение системы отсчета не влияет на механические процессы, происходящие в системе материальных точек – механический принцип относительности.
По второму закону Ньютона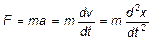 
.
Специальная — значит частный случай для очень слабых гравитационных полей. Энштейн сформулировал постулаты:
1. Никакие опыты (механические, электрические, оптические) проводимые внутри данной инерциальной системы отсчета не дают возможности обнаружить, находится ли эта система в состоянии покоя или равномерно движется. (Обобщение принципа Галилея на все физические явления). Принцип относительности.
2. Принцип инвариантности скорости света. Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и поэтому одинакова во всех инерциальных системах.
Постоянство скорости света — фундаментальное свойство природы.
Преобразования Лоренца
Если в классической механике законы инвариантны относительно преобразований Галилея, то в случае электромагнетизма, оказалось, что фундаментальная система уравнений, описывающих электромагнитные явления (уравнения Максвелла) не инвариантны относительно этих преобразований. В этой связи Лоренцем были найдены преобразования, оставляющие систему уравнений Максвелла инвариантной.
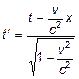Оказалось, что эти преобразования имеют вид:
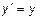
Физический смысл этим уравнениям дал Эйнштейн, и это было началом создания теории относительности. В частности, преобразования Лоренца приводят к выводу, что понятия длина и время разные в разных системах отсчета, и это не просто умозаключение, а подтверждается экспериментально. Из преобразований Лоренца для 
легко видеть, что они переходят в преобразования Галилея.
В классической механике наряду с преобразованиями Галилея справедлив классический закон сложения скоростей: 
.
Выведем формулу для преобразования скорости, использую преобразования Лоренца для координат и времени.
; 
.
; 
.
.
Из этой формулы можно показать, что скорость света c является предельной. Пусть 
, тогда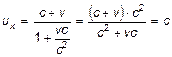 
.
Понятие одновременности. Относительность длины и промежутков времени.
Будем рассматривать два события в системе К и К¢.
1)Если события в системе координат К происходят одновременно (t1=t2) и в одном месте (x1=x2), то в соответствии с преобразованиями Лоренца в любой другой системе К¢ они также будут одновременными и совпадающими в пространстве 
.
2)Если события одновременны t1=t2, но разнесены в пространстве x1¹x2, то в системе координат К¢:
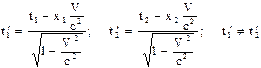
т.о. в системе К¢ события разнесены в пространстве и во времени. Какое из них первое, а какое второе?
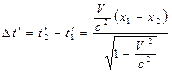т.к. t1=t2, зависит от знака (x2-x1)
3)Теперь пусть события в одном месте, но в разное время x1=x2; t1¹t2 (или одно длительное событие)
;(т.к. x1=x2) Þ
Т.е. с точки зрения наблюдателя в неподвижной системе интервал времени по часам движущейся системы будет больше, т.е. события разворачиваются медленнее в движущейся системе. Парадокс близнецов.
Или длительность события, происходящего в некоторой точке наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
4)Рассмотрим стержень длины 
, покоящийся в системе К¢. Какая его длина в системе К? В системе К он будет пролетать мимо наблюдателя со скоростью v=V. Нужно замерить его длину, т.е. отметить координаты x1 и x2 одновременно! т.е. t1=t2=t
Тогда 
Т.о. длина стержня в неподвижной системе наибольшая, остальные размеры не меняются т.к.
Релятивистский импульс и релятивистская масса.
В классической механике 
.
Закон сохранения импульса — фундаментальный закон природы, т. е. в любой замкнутой системе векторная сумма импульсов всех тел системы постоянна.
Оказывается, чтобы этот фундаментальный закон выполнялся и в теории относительности необходимо определить 
. Выражение 
— релятивистская масса. Зависимость 
выглядит следующим образом:
.
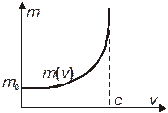Основное уравнение релятивистской динамики
В выражении для импульса значение массы зависит от скорости движения тела, поэтому если в выражение 
подставить значение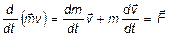 
, то получится 
.
В классическом виде вектор силы и вектор ускорения имеют одинаковые направления, а в релятивистской механике это не так.
Релятивистское выражение для кинетической энергии. Взаимосвязь массы и энергии
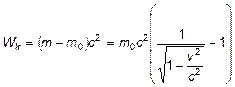
— Закон взаимосвязи массы и энергии
Закон взаимосвязи массы и энергии: полная энергия системы равна произведению релятивистской массы системы на квадрат скорости света в вакууме 
.
Наряду со специальной (частной) теорией относительности Эйнштейн заложил основы общей теории относительности — теории гравитации. Закон Ньютона взаимодействия тел не может быть применен в теории относительности, т. к. он описывает взаимодействия тел с бесконечной скоростью.
Некоторые следствия:
1. Искривление хода луча вблизи массивных тел.
2. Замедление хода часов в гравитационном поле.
3. Существование черных дыр.
