
Прежде чем можно будет что-либо сказать о теории тяготения Эйнштейна, необходимо сделать несколько очень кратких замечаний относительно четырехмерной неевклидовой геометрии. Герман Минковский, польский математик, дал теории относительности изящную интерпретацию в терминах четырехмерного пространства — времени. Многие идеи этой главы в такой же мере принадлежат Минковскому, как и Эйнштейну.
Рассмотрим геометрическую точку. Она не имеет размера. При движении вдоль прямой она порождает линию, имеющую одно измерение. Будем двигать прямую под прямым углом к ней самой, и она создаст плоскость, имеющую два измерения. Если двигать плоскость под прямым углом к ней самой, то она образует трехмерное пространство. И это тот предел, до которого мы можем дойти в своем воображении.

Но математик представляет себе (не в том смысле, что он создает в своем воображении какую-то картину, а в том смысле, что он разрабатывает математический аппарат) движение трехмерного пространства в направлении, перпендикулярном всем его трем измерениям. Это порождает четырехмерное евклидово пространство. Нет никакой необходимости останавливаться на четырех. Мы можем переходить к пространствам пяти, шести, семи или более измерений. Все эти пространства евклидовы. Они представляют собой развитие евклидовой геометрии точно так же, как евклидова стереометрия является развитием евклидовой планиметрии.
Евклидова геометрия основана на нескольких аксиомах, одной из которых является знаменитая аксиома о параллельных прямых. Она гласит, что на плоскости через данную точку, расположенную вне данной прямой, можно провести одну и только одну прямую, параллельную этой прямой.

Говорят, что евклидова поверхность, на которой выполняется этот постулат, плоская. Она имеет нулевую кривизну и бесконечную площадь. Неевклидова геометрия — это такая геометрия, в которой аксиома о параллельных прямых заменена другой аксиомой. При этом возможны два существенно различных случая.
В первом случае, называемом эллиптической геометрией, говорится, что на поверхности через данную точку, расположенную вне заданной линии, не может быть проведено ни одной параллельной ей линии. Поверхность сферы представляет собой грубую, неточную модель неевклидовой поверхности такого типа. «Наиболее прямой» линией на сфере является большой круг (круг с диаметром, равным диаметру сферы). Все большие круги пересекаются друг с другом, и поэтому невозможно, чтобы два больших круга были параллельны. Говорят, что неевклидова поверхность этого типа имеет положительную кривизну. Такая кривизна приводит к тому, что поверхность замыкается сама на себя. Она имеет конечную, а не бесконечную площадь.

Неевклидова геометрия другого типа, называемая гиперболической, — это геометрия, в которой евклидов постулат о параллельных прямых заменен постулатом, гласящим, что на поверхности через точку, расположенную вне данной линии, проходит бесконечное множество параллельных ей линий. Грубой моделью части поверхности такого типа является седловидная поверхность. Говорят, что такая поверхность имеет отрицательную кривизну. Она не замыкается сама на себя. Подобно евклидовой плоскости, она тянется до бесконечности во всех направлениях.
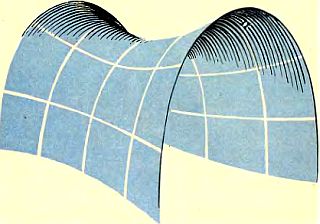
И эллиптическая, и гиперболическая геометрии представляют собой геометрии поверхностей постоянной кривизны. Это означает, что кривизна везде одна и та же, объекты не претерпевают искажений при переходе из одной точки в другую. Неевклидова геометрия более общего типа, обычно называемая римановой геометрией, это такая геометрия, в которой кривизна может меняться от точки к точке любым заданным образом.

Точно так же, как имеются евклидовы геометрии пространств 2, 3, 4, 5, 6, 7…. измерений, существуют неевклидовы геометрии 2, 3, 4, 5, 6, 7…. измерений.
При разработке общей теории относительности Эйнштейн счел необходимым использовать четырехмерную риманову геометрию. Однако вместо четвертого пространственного измерения Эйнштейн выбрал в качестве четвертого измерения время. В понятии четвертого измерения нет ничего таинственного или мистического. Просто это означает, что каждое событие, которое имеет место во Вселенной, представляет собой событие, происходящее в четырехмерном мире пространства — времени.
Это можно уяснить себе, рассмотрев следующее событие. Вы садитесь в автомобиль в 2 часа дня и едете из своего дома в ресторан, расположенный в 3 км к югу и в 4 км к востоку от вашего дома. На двухмерной плоскости кратчайшее расстояние от вашего дома до ресторана есть гипотенуза прямоугольного треугольника со сторонами 3 и 4 км. Эта гипотенуза имеет длину 5 км.
Но вам требуется также затратить какое-то время, скажем 10 мин, на поездку. Этот промежуток времени может быть изображен на трехмерном графике. Одна координата на этом графике есть расстояние к югу в километрах, другая — расстояние к востоку в километрах, а координата по вертикали — время в минутах. На трехмерном графике пространства — времени «интервал» (пространственно-временной промежуток) между двумя событиями (вашим отъездом из дому и прибытием к ресторану) изображен в виде прямой.

Эта прямая линия не есть график реальной поездки. Просто она является мерой пространственновременного расстояния между двумя событиями.
График поездки может быть сложной кривой, поскольку ваша машина ускоряется в начале движения, расположение улиц может сделать невозможной поездку к ресторану по прямой, где-то в пути вы остановитесь при красном свете, и, наконец, вы должны испытать отрицательное ускорение, когда останавливаете машину. Сложный волнистый график реальной поездки в теории относительности называется «мировой линией» поездки. В рассмотренном случае это мировая линия в трехмерном пространстве — времени, или (как его иногда называют) в трехмерном пространстве Минковского.

Так как эта поездка на автомобиле происходила на плоскости, имеющей два измерения, оказалось возможным добавить еще одно измерение — временное и изобразить ее в виде трехмерного графика.
Когда события происходят в трехмерном пространстве, невозможно нарисовать график в четырехмерном пространстве — времени, но математики умеют обращаться с такими графиками, не рисуя их. Попытайтесь представить себе четырехмерного ученого, который умеет чертить четырехмерные графики с такой же легкостью, как обычный ученый чертит двух- и трехмерные графики. Три координаты его графика соответствуют трем измерениям нашего пространства. Четвертая координата — это наше время. Если космический корабль улетает с Земли и приземляется на Марсе, наш воображаемый ученый изобразит мировую линию этого путешествия в виде кривой на своем четырехмерном графике. (Линия будет кривой, так как корабль не может проделать такое путешествие без ускорений.) Пространственно-временной «интервал» между отлетом и приземлением будет изображаться на этом графике прямой линией.
В теории относительности всякий предмет представляет собой четырехмерную структуру, движущуюся вдоль мировой линии в четырехмерном мире пространства — времени. Если какой-либо предмет рассматривается покоящимся по отношению к трем пространственным координатам, он все равно движется во времени. Его мировая линия будет прямой, параллельной временной оси графика. Если предмет совершает равномерное движение в пространстве, его мировая линия по-прежнему будет прямой, но теперь уже непараллельной оси времени. Если предмет движется неравномерно, его мировая линия становится кривой.
Теперь мы можем рассмотреть Лоренц-Фитцджеральдово сокращение специальной теории с новой точки зрения: с точки зрения Минковского, иначе говоря, с точки зрения нашего четырехмерного ученого. Как мы видели, когда два космических корабля проходят один мимо другого, находясь в состоянии относительного движения, наблюдатели на каждом из кораблей обнаруживают некоторые изменения формы другого корабля, а также изменения скорости хода часов на другом корабле. Это происходит по той причине, что пространство и время не являются абсолютными величинами, не зависящими друг от друга. Они похожи, так сказать, на теневые проекции четырехмерных пространственно-временных предметов. Если поставить книгу против источника света и проектировать ее тень на двухмерную стенку, то, поворачивая книгу, можно изменять форму ее тени. В одном положении тень книги представляет собой широкий прямоугольник, в другом — узкий. Книга не меняет своей формы, меняются только ее двухмерные тени.

Подобным образом наблюдатель видит четырехмерную структуру, скажем, космический корабль, в различных трехмерных проекциях в зависимости от того, как он движется по отношению к кораблю. В некоторых случаях проекция занимает больше пространства и меньше времени, в других случаях наоборот. Изменения, которые он наблюдает в пространственных и временных измерениях другого корабля, могут быть объяснены своего рода «поворотом» корабля в пространстве — времени, приводящим к изменению его теневых проекций на пространство и время. Именно это имел в виду Минковский, когда (в 1908 г.) начал знаменитую лекцию на 80-м съезде германского общества натуралистов и физиков. Эта лекция опубликована в книге «Принцип относительности» Альберта Эйнштейна и др. Никакая из популярных книг по теории относительности не будет полной без следующей цитаты из лекции Минковского:
«Взгляды на пространство и время, которые я хочу изложить перед вами, развивались на основе экспериментальной физики, и в этом их сила. Они радикальны. Отныне пространство само по себе и время само по себе обратились в простые тени, и только какое-то единство их обоих сохранит независимую реальность».
Отсюда следует понять, что пространственно-временная структура, четырехмерная структура космического корабля, остается такой же твердой и неизменной, как в классической физике. В этом состоит существенное различие между отброшенной теорией сокращения Лоренца и теорией сокращения Эйнштейна. Для Лоренца сокращение представляло собой реальное сокращение трехмерного предмета. Для Эйнштейна «реальный» предмет — это четырехмерный предмет, который никак не меняется. Его трехмерная проекция на пространство и его одномерная проекция на время могут изменяться, но четырехмерный корабль в пространстве — времени остается неизменным.
Это другой пример того, как теория относительности вводит новые абсолюты. Четырехмерная форма твердого тела абсолютна и неизменна. Подобно этому, четырехмерный интервал между двумя событиями в пространстве—времени есть абсолютный интервал. Наблюдатели, движущиеся с большими скоростями в разных состояниях относительного движения, могут расходиться во мнении о том, насколько удаленными друг от друга в пространстве представляются им два события и как они разделены во времени, но все наблюдатели независимо от их движения, будут едины в том, насколько разделены эти два события в пространстве — времени.
В классической физике тело, если на него не действует сила, движется в пространстве вдоль прямой с постоянной скоростью. Например, планета двигалась бы по прямой, если бы ее не удерживала сила притяжения к Солнцу. Таким образом. Солнце заставляет планету двигаться по эллиптической орбите.
В теории относительности тело, пока на него не действуют силы, также движется по прямой с постоянной скоростью, но эта прямая должна рассматриваться как линия в пространстве — времени, а не в пространстве. Все это справедливо даже при наличии тяготения. Дело в том, что тяготение, согласно Эйнштейну, вовсе не является силой! Солнце не «притягивает» планеты. Земля не «притягивает» вниз падающее яблоко. Просто большое материальное тело, такое, как Солнце, приводит к искривлению пространства — времени в окружающей его области.
Чем ближе к Солнцу, тем больше кривизна. Иными словами, структура пространства — времени в окрестности больших материальных тел становится неевклидовой. В этом неевклидовом пространстве тела продолжают выбирать возможные наиболее прямые пути, но то, что является прямым в пространстве — времени, изображается кривой линией, когда проектируется на пространство. Наш воображаемый ученый, если бы он изображал орбиту Земли на своем четырехмерном графике, представил бы ее в виде прямой линии. Мы, будучи трехмерными существами (точнее, существами, которые разделяют пространство—время на трехмерное пространство и одномерное время), видим ее путь в пространстве в виде эллипса.

Авторы, пишущие о теории относительности, часто объясняют это следующим образом. Представим себе плоский кусок резины, натянутый на прямоугольную рамку. Апельсин, положенный на этот кусок, создает впадину. Мраморный шарик, помещенный вблизи апельсина, будет скатываться к нему. Апельсин не «притягивает» шарик. Он создает поле (впадину) такой структуры, что шарик, выбирая путь наименьшего сопротивления, скатывается к нему.

Грубо (очень грубо) подобным же образом пространство — время искривляется в присутствии больших масс, таких, как Солнце. Это искривление и есть поле тяготения. Планета, движущаяся вокруг Солнца, движется по эллипсу не потому, что Солнце притягивает ее, а благодаря особым свойствам поля; в этом поле эллипс представляет собой наиболее прямой путь, по которому планета может двигаться в пространстве — времени.
Такой путь называется геодезической линией.

Это слово настолько важно в теории относительности, что его следует объяснить более подробно. На евклидовой плоскости, такой, как ровный лист бумаги, наиболее прямая линия между двумя точками есть прямая линия. Она является также кратчайшим расстоянием. На поверхности шара геодезическая линия между двумя точками есть дуга большого круга. Если натянуть веревку между этими точками, она отметит геодезическую линию. Последняя также представляет собой наиболее прямое и кратчайшее расстояние между двумя точками.
В четырехмерной евклидовой геометрии, где все измерения являются пространственными измерениями, геодезическая линия также есть кратчайшая и наиболее прямая линия, соединяющая две точки. Но в неевклидовой геометрии пространства — времени Эйнштейна это все не так просто. Имеется три пространственных измерения и одно временное измерение, объединенные согласно уравнениям теории относительности. Эти уравнения таковы, что геодезическая линия, хотя она по-прежнему остается наиболее прямым путем в пространстве—времени, есть длиннейшее, а не кратчайшее расстояние.

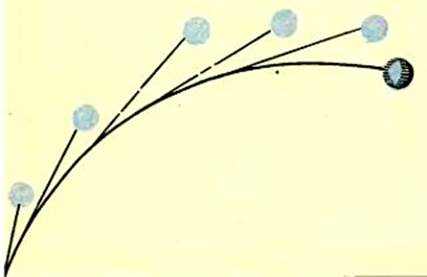
Это понятие невозможно объяснить, не прибегая к сложному математическому аппарату, но последний дает следующий курьезный результат. Тело, движущееся под действием только тяготения, всегда выбирает такой путь, на прохождение которого требуется наибольшее время, если последнее измеряется по его собственным часам. Бертран Рассел назвал это «законом космической лени». Яблоко падает по прямой вниз, ракета движется по параболе. Земля движется по эллипсу потому, что они «слишком ленивы», чтобы выбрать другие пути.
Именно этот закон космической лени заставляет тела двигаться в пространстве — времени так, что иногда это движение объясняют инерцией, а в других случаях тяготением. Если вы привяжете веревку к яблоку и закрутите ее по кругу, веревка не даст яблоку двигаться по прямой линии. Мы говорим, что инерция яблока натягивает веревку. Если веревка разорвется, яблоко полетит по прямой.

Нечто подобное происходит, когда яблоко падает с дерева. До того как оно упадет, ветка не дает ему двигаться по четырехмерной прямой. Яблоко на ветке покоится (по отношению к Земле), но оно движется во времени, так как непрерывно зреет. Если бы не было поля тяготения, это продвижение вдоль временной координаты изображалось бы прямой линией на четырехмерном графике. Но земное притяжение искривляет пространство — время в окрестностях яблока. Вследствие этого мировая линия яблока становится кривой. Когда яблоко срывается с ветки, оно продолжает двигаться в пространстве — времени, но (будучи ленивым яблоком) теперь выпрямляет свой путь и выбирает геодезическую линию. Мы видим эгу геодезическую линию как линию, по которой падает яблоко, и приписываем падение притяжению. Однако, если бы захотели, мы могли бы сказать, что инерция яблока, после того как оно внезапно было сброшено со своего искривленного пути, привела его на Землю.
Допустим, что после того, как яблоко упало, мимо проходил мальчишка и поддал его босой ногой.
Он вскрикнул от боли, так как ушиб пальцы. Последователь Ньютона сказал бы, что инерция яблока сопротивлялась этому удару. Последователь Эйнштейна может сказать то же самое, но он может также сказать, если ему это больше нравится, что пальцы на ноге мальчишки заставили весь космос (включая и пальцы) ускоряться в обратном направлении, а это привело к созданию поля тяготения, которое с большой силой притянуло яблоко к пальцам. Все это вопрос формулировки. Математически эта ситуация описывается одной системой пространственно-временных уравнений поля, но о ней можно говорить (благодаря принципу эквивалентности) на языке любой из двух ньютоновских формулировок (гравитация, инерция).

Хотя теория относительности заменяет тяготение геометрическим искривлением пространства — времени, она оставляет без ответа многие важные вопросы. Происходит это искривление мгновенно во всем пространстве или распространяется подобно волнам? Большинство физиков считает, что искривление движется подобно волне и это движение происходит со скоростью света. Высказано даже предположение, что гравитационные волны состоят из крошечных неделимых частиц, обладающих конечной энергией и называемых «гравитонами». До сих пор, однако, ни один эксперимент не обнаружил ни волн, ни гравитонов.
Роберт Дик, физик из Принстонского университета, считает, что тяготение постепенно становится слабее и, возможно, в настоящее время оно на 13 процентов меньше, чем было четыре или пять миллиардов лет назад, когда образовалась Земля. Если это так, то Земля, вероятно, расширяется и ее поверхность трескается при этом процессе. Солнце также должно было бы расширяться. Два миллиарда лет назад оно должно было быть меньше, плотнее и горячее: этот факт мог бы объяснить тропические условия, которые господствовали на большей части Земли в ранние геологические эпохи. Все эти соображения в настоящее время являются только догадками, но, может быть, скоро удастся поставить эксперимент по проверке теории Дика.
Теория относительности дает новый способ рассмотрения и описания тяготения, но оно по-прежнему остается таинственным, малопонятным явлением.
Никто не знает, как оно связано и связано ли вообще с электромагнетизмом. Эйнштейн и другие пытались разработать «теорию единого поля», которая объединила бы тяготение и электромагнетизм в одной системе математических уравнений. Результаты оказались неутешительными. Может быть, какой-нибудь юный читатель этих строк, если он обладает творческим гением Эйнштейна, когда-нибудь поймет, как сформулировать такую теорию.
Была ли подтверждена экспериментальными данными общая теория относительности? Да, хотя и не так полно, как специальная теория относительности. Одно подтверждение было получено при изучении орбиты Меркурия — ближайшей к Солнцу планеты. Орбита Меркурия представляет собой эллипс, но сам эллипс медленно поворачивается. С помощью уравнений тяготения Ньютона можно объяснить это, если учесть влияние других планет, но предсказываемое при этом вращение получается немного более медленным, чем наблюдаемое в действительности. Уравнения Эйнштейна предсказывают вращение эллиптической орбиты планеты даже в отсутствие других планет; в случае Меркурия предсказанная орбита значительно ближе к действительной, чем орбита, предсказанная Ньютоном. Орбиты других планет гораздо более близки к круговым, поэтому этот эффект труднее наблюдать, но в последние годы были проведены измерения вращения орбит Венеры и Земли, которые находятся в хорошем согласии с уравнениями Эйнштейна.
Второе предсказание, сделанное Эйнштейном, состояло в том, что в спектре Солнца должно наблюдаться очень небольшое смещение в сторону красного края. Согласно уравнениям общей теории сильные поля тяготения оказывают замедляющее действие на время. Это означает, что любой ритмический процесс, такой, как колебания атома или тикание часов, на Солнце будет идти с немного меньшей скоростью, чем на Земле. В свою очередь это приведет к сдвигу спектра Солнца в сторону более длинных волн, что даст покраснение спектра. Такой сдвиг наблюдался, но он не является очень сильным подтверждением, так как ему можно дать очень много других объяснений.[4] Белая звезда — карлик, очень близкая к Сириусу, известная как спутник Сириуса, обладает массой, достаточной для того, чтобы создать красное смещение, в тридцать раз большее, чем Солнце. Оно также наблюдалось и является более сильным подтверждением. Однако самое сильное подтверждение действия тяготения на время было получено недавно в лаборатории. О нем будет рассказано в конце гл. 8.
Наиболее сенсационная из всех проверок общей теории была проведена в 1919 г. во время полного затмения Солнца. Эйнштейн рассуждал следующим образом. Если лифт в межзвездном пространстве идет вверх с увеличивающейся скоростью, то луч света, идущий внутри лифта от стены к стене, будет отклоняться вниз, двигаясь по параболическому пути. Это можно объяснить инерцией, но согласно общей теории можно считать лифт неподвижной системой отсчета и рассматривать искривление луча как результат действия тяготения.

Таким образом, тяготение может искривлять световые лучи. Это искривление слишком ничтожно, чтобы его можно было зарегистрировать с помощью какого-либо опыта, проводимого в лаборатории, но оно может быть измерено астрономами во время полного затмения Солнца. В результате того что солнечный свет задерживается Луной, звезды, расположенные вблизи края Солнца, становятся видимыми. Свет от этих звезд проходит через самую сильную часть поля тяготения Солнца. Любой сдвиг в видимых положениях этих звезд указывал бы на то, что тяготение Солнца изгибает путь света. Чем больше сдвиг, тем больше изгиб.
Следует помнить о следующем. Когда вы читаете об «искривлении» света в результате действия тяготения или инерции, вы должны иметь в виду, что это только трехмерный способ описания явления. В пространстве путь света действительно искривляется. Но в четырехмерном мире Минковского пространства — времени свет, так же как и в классической физике, по-прежнему движется вдоль геодезической линии. Он выбирает возможный наиболее прямой путь. Наш воображаемый четырехмерный ученый на своей карте пространства — времени всегда изображал бы путь луча света прямой линией даже в том случае, если он проходит через сильные поля тяготения.

Эддингтон, английский астроном, возглавлял экспедицию ученых, которая в 1919 г. прибыла в Африку наблюдать полное затмение Солнца. Главной целью этой экспедиции было провести точные измерения положений звезд, расположенных вблизи солнечного диска. Физика Ньютона также предсказывала искривление света в поле тяготения, но уравнения Эйнштейна давали примерно вдвое большее отклонение. Таким образом, были возможны по крайней мере три различных результата опыта:
1. Изменений в положениях звезд могло не произойти.
2. Отклонение могло быть близко к тому, что предсказала физика Ньютона.
3. Отклонение могло быть близко к тому, что предсказал Эйнштейн.
Первый результат ниспровергал бы как уравнения Ньютона, так и уравнения общей теории относительности. Второй говорил бы в пользу Ньютона и против Эйнштейна. Третий говорил бы против Ньютона и в пользу Эйнштейна. Согласно популярному в то время анекдоту, два астронома из этой экспедиции обсуждали все три возможности.
«А что, — сказал один из них, — если мы получим отклонение, вдвое большее предсказанного Эйнштейном?»
«Тогда, — сказал другой, — Эддингтон сойдет с ума».
К счастью, отклонение оказалось близко к предсказанию Эйнштейна. Широкая реклама, созданная вокруг экспедиции Эддингтона, впервые привлекла внимание широкой публики к общей теории относительности. Сегодня астрономы скептически относятся к этому подтверждению. Трудности при проведении точных измерений положений звезд во время затмения оказались значительно большими, чем предполагал Эддингтон. Результаты, полученные во время различных затмений, наблюдавшихся после 1919 г., были несколько отличными. На конференции Королевского общества в Лондоне в феврале 1962 г. группа ученых обсудила этот вопрос. Они пришли к заключению, что так как трудности очень велики, то наблюдающим затмения не стоит больше пытаться проводить такие измерения.
Несмотря на то что имеются опыты (все-таки их немного), подтверждающие общую теорию относительности, и огромное число опытов, еще не проводившихся и даже не обсуждавшихся, которые могли бы подтвердить ее еще лучше, возможны эксперименты, которые могли бы сильно дискредитировать эту теорию. Георгий Гамов, хорошо известный физик из Колорадского университета, описал один такой эксперимент, в котором участвуют античастицы.
Как мы уже говорили, последние представляют собой элементарные частицы, во всем подобные частицам обычной материи, но имеющие противоположный электрический заряд. Некоторые ученые считают, что античастицы могут иметь отрицательную массу. Если это так, любая действующая на них сила будет ускорять их в отрицательном направлении.
Антияблоко, сделанное из антиматерии, улетело бы в небеса, вместо того чтобы упасть на нос Ньютону.

Имеют античастицы отрицательную массу или нет, пока не установлено, но если это так, теория относительности окажется перед серьезными затруднениями.
Чтобы понять, почему должны появиться трудности, представим себе космический корабль, покоящийся по отношению к звездам. В центре одного из его отсеков плавает одно антияблоко с отрицательной массой. Корабль начинает двигаться в направлении к потолку с ускорением в одно g (g — это ускорение, с которым тела падают на Землю, равное примерно 9,8 м/сек за 1 сек. Последнее означает, что каждую секунду скорость увеличивается на 9,8 м/сек).
Что произойдет с яблоком?
С точки зрения наблюдателя вне корабля, связанного с инерциальной системой космоса, яблоко по отношению к звездам должно остаться на том же самом месте, где оно было. На него не действует никакая сила. Корабль не прикасается к яблоку, он мог бы вообще находиться очень далеко от него.
Следовательно, пол отсека будет двигаться вверх до тех пор, пока не ударится в яблоко. (В этом мысленном эксперименте мы не беспокоимся о том, что случится, когда пол ударится об яблоко.)
Ситуация полностью изменится, если принять корабль в качестве неподвижной системы отсчета.

Теперь наблюдатель должен предположить наличие поля тяготения, действующего внутри корабля. Это поле пошлет яблоко к потолку с ускорением (по отношению к звездам) два g. Основной принцип относительности нарушается. Две системы отсчета не взаимозаменяемы.
Иными словами, понятие отрицательной массы нелегко примирить с общей теорией относительности, тогда как ньютоновский подход к инерции свободно его допускает. Классическая физика попросту принимает первую точку зрения. Корабль находится в абсолютном движении относительно эфира. Яблоко остается в абсолютном покое. Не появляется никаких полей тяготения, которые запутали бы эту картину.
Открытие отрицательной массы и сопровождающего ее эффекта антигравитации, заключает Гамов, «заставило бы нас выбирать между законом инерции Ньютона и принципом эквивалентности Эйнштейна. Автор горячо надеется, что этого никогда не будет».






