
Длина и время, как было показано в предыдущей главе, являются относительными понятиями.
Если один космический корабль пролетает мимо другого с постоянной скоростью, то наблюдатели на каждом из кораблей найдут, что космонавты на другом корабле похудели и передвигаются медленнее. Если их относительная скорость достаточно велика, то движения их коллег будут напоминать движения актеров в замедленной кинокартине. Все явления с периодическим движением будут казаться замедленными: движение маятника и балансира в часах, пульсация сердца, колебание атомов и т. д.
По словам Артура Стэнли Эддингтона, выдающегося английского астронома, который стал одним из самых первых и наиболее ревностных последователей Эйнштейна, будет казаться, что даже сигары на другом корабле тлеют дольше. Космонавт ростом в два метра, стоящий в горизонтально движущемся корабле, по-прежнему будет выглядеть двухметровым, но его тело будет казаться тоньше в направлении движения. Когда же он ляжет, вытянувшись в направлении движения корабля, восстановится нормальная ширина его тела, но теперь будет казаться, что его рост уменьшился в направлении от головы до пят.

Если бы два космических корабля действительно смогли двигаться один относительно другого со скоростью, достаточно большой, чтобы сделать подобные изменения существенными, то всевозможные трудности технического характера не позволили бы наблюдателям на каждом корабле увидеть эти изменения. Писатели любят пояснять теорию относительности упрощенными эффектными примерами. Эти цветистые иллюстрации не описывают изменений, которые действительно можно было бы наблюдать либо человеческим глазом, либо с помощью любых приборов, известных в настоящее время. О существовании этих изменений космонавты смогли бы в принципе узнать на основе измерений, если бы были достаточно хорошие измерительные приборы.
В дополнение к изменениям длины и времени имеется также релятивистское изменение массы.
Масса, грубо говоря, — это мера количества вещества в теле.
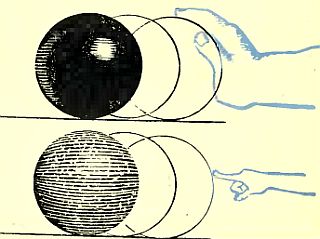
Свинцовый и пробковый шары могут иметь одинаковые размеры, но свинцовый шар более массивен. Концентрация вещества в нем выше.
Существует два способа измерения массы тела: либо взвешиванием, либо по тому, насколько велика сила, необходимая, чтобы сообщить этому телу определенное ускорение. Первый метод не очень хорош, поскольку получаемые результаты зависят от силы тяжести в данном месте. Свинцовый шар, поднятый на вершину высокой горы, будет весить несколько меньше, чем у ее подножия, хотя его масса останется в точности той же самой. На Луне его вес был бы значительно меньше, чем на Земле. На Юпитере же его вес оказался бы значительно больше.
Второй метод измерения массы дает одинаковые результаты независимо от того, проводились они на Земле, на Луне или на Юпитере; однако при использовании этого метода сразу же возникают курьезные вопросы. Чтобы определить этим методом массу движущегося тела, нужно измерить силу, которая необходима для сообщения ему определенного ускорения. Ясно, что для того, чтобы заставить катиться пушечное ядро, необходим более сильный толчок, чем для пробкового шара. Масса, измеренная таким методом, называется инертной массой в отличие от гравитационной массы или веса. Подобные измерения не могут быть выполнены без измерений времени и расстояний. Инертная масса пушечного ядра, например, выражается через величину силы, необходимой для увеличения его скорости (расстояние в единицу времени) на столько-то в единицу времени. Как мы видели ранее, измерения времени и расстояний меняются с изменением относительной скорости тела и наблюдателя. Как следствие этого меняются также результаты измерений инертной массы.
В гл. 6 мы вернемся к понятию гравитационной массы и ее связи с инертной массой. Здесь же пойдет речь только об инертной массе, полученной в результате измерений, выполняемых каким-либо наблюдателем. Для наблюдателей, покоящихся относительно предмета, например для космонавтов, везущих в космическом корабле слона, инертная масса предмета остается одной и той же независимо от скорости корабля. Масса слона, измеряемая подобными наблюдателями, называется его собственной массой или массой покоя. Инертная масса того же самого слона, измеренная каким-либо наблюдателем, движущимся относительно этого слона (например, наблюдателем на Земле), называется релятивистской массой слона. Масса покоя тела никогда не меняется, а релятивистская масса изменяется. Оба измерения являются измерениями инертной массы.

В этой главе будет идти речь только об инертной массе; когда употребляется слово «масса», его следует понимать именно в этом смысле.
Все три переменные — длина, время, масса—охватываются одним и тем же выражением для лоренцовского сокращения

Длина и скорость хода часов меняются по одному и тому же закону, так что формула для этих величин одна и та же.
В то же время масса и длина временных интервалов меняются по обратным законам, а это означает, что формулу здесь следует написать так:

Масса любого тела, измеренная наблюдателем, движущимся равномерно относительно этого тела, получается умножением массы покоя тела на приведенное выше выражение (где v — относительная скорость объекта; с — скорость света).
Например, если относительная скорость двух космических кораблей составляет 260 000 км/сек, наблюдатели на каждом из кораблей будут считать, что другой корабль вполовину короче, часы на нем идут в два раза медленнее, продолжительность часа в два раза длиннее и масса корабля в два раза больше. Конечно, эти космонавты на своем собственном корабле найдут все совершенно нормальным. Если бы эти корабли смогли достичь относительной скорости, равной скорости света, наблюдатели на каждом из кораблей считали бы, что другой корабль сократил свою длину до нуля, приобрел бесконечную массу в что время на другом корабле замедлилось до полной остановки!
Если бы инертная масса не менялась указанным выше образом, то непрерывное действие силы, такой, например, как сила, развиваемая ракетными двигателями, могло бы поддерживать возрастание скорости корабля до тех пор, пока эта скорость не превысила бы скорости света. Но этого не произойдет, поскольку по мере того, как корабль движется все быстрее и быстрее (с точки зрения, скажем, наблюдателя на Земле), его релятивистская масса все время возрастает в той же пропорции, в которой уменьшается его длина и замедляется время. Когда корабль сократится до одной десятой своей первоначальной длины, его релятивистская масса увеличится в десять раз. Он окажет в десять раз большее сопротивление своим ракетным двигателям; следовательно, потребуется в десять раз большая сила, чем в случае покоящегося корабля, чтобы обеспечить одно и то же увеличение скорости. Скорость света никогда не может быть достигнута. Если бы она была достигнута, внешний наблюдатель нашел бы, что корабль сократил свою длину до нуля, приобрел бесконечную массу, а его ракетные двигатели действуют с бесконечно большой силой.
Космонавты внутри корабля не обнаружили бы у себя никаких изменений, но они видели бы все в космосе проносящимся назад со скоростью света, космическое время — остановившимся, каждую звезду — сплющенной до диска и бесконечно массивной.
Только у авторов научно-фантастических произведений хватает отваги размышлять на тему о том, что смогут увидеть космонавты, если удастся каким-либо образом пробить световой барьер. Возможно, космос показался бы вывернутым наизнанку и превратившимся в свое собственное зеркальное изображение, звезды приобрели бы отрицательную массу, а космическое время пошло бы назад. Спешу добавить, что ни одно из этих явлений не следует из формул специальной теории относительности. Если скорость света превышена, эти формулы дают такие значения длины, времени и массы, которые являются, как говорят математики, «мнимыми числами»: числами, которые содержат квадратный корень из минус единицы. Кто знает? Может быть, корабль, преодолевший световой барьер, влетел бы прямо в Страну волшебника Гудвина!

Выучив, что ничто не может обогнать свет, студенты, начинающие изучение теории относительности, часто оказывались сбитыми с толку, встретив упоминание о скоростях, больших скорости света.
Чтобы ясно понять, что должна дать теория относительности в этом случае, лучше всего будет ввести термин «инерциальная система отсчета». (Более ранние авторы трудов по теории относительности называли ее «инерциальной системой», или «галилеевой системой».) Когда какое-либо тело вроде космического корабля движется равномерно, то говорят, что это тело и все прочие объекты, движущиеся вместе с ним в том же направлении и с той же скоростью (как, например, все объекты внутри корабля), связаны с одной и той же инерциальной системой отсчета. (Инерциальная система отсчета есть декартова система координат, с которой связан этот космический корабль.) Вне связи с определенной инерциальной системой отсчета специальная теория относительности более не применима, и существует много возможностей наблюдать скорости, превышающие скорость света.
Рассмотрим, например, такой простой случай.
Космический корабль, движущийся со скоростью в три четверти скорости света, пролетает над вами, двигаясь точно на восток. В тот же момент другой космический корабль, двигающийся с такой же скоростью, пролетает над вами, направляясь прямо на запад. В вашей системе отсчета, связанной с инерциальной системой отсчета Земли, эти два корабля пролетают один мимо другого с относительной скоростью, равной полутора скоростям света. Они сближаются с этой скоростью и разлетаются с этой скоростью. Ничто в теории относительности не запрещает этого. Однако специальная теория относительности настаивает на том, что если вы летите в одном из кораблей, то, вычислив относительную скорость этих кораблей, вы должны получить значение меньше скорости света.
Мы приложили все усилия, чтобы избежать применения математического аппарата теории относительности и этой книге, но, подобно формуле лоренцевского сокращения, даваемая ниже формула слишком проста, чтобы ее не привести. Если х — скорость одного корабля относительно Земли, а у — скорость другого корабля относительно Земли, то скорость этих кораблей друг относительно друга, как она представляется с Земли, будет, конечно, равна х плюс у. Но, оказавшись на месте наблюдателя на любом из этих кораблей, мы должны складывать скорости по следующей формуле:

В этой формуле с — скорость света. Легко видеть, что, когда скорости кораблей малы сравнительно со скоростью света, эта формула дает результат, почти совпадающий с тем, что получается при сложении двух скоростей обычным способом.
Но если скорости кораблей очень велики, эта формула дает совершенно отличный результат. Возьмем предельный случай и предположим, что вместо космических кораблей имеются два луча света, проходящих над нами в противоположных направлениях. Земной наблюдатель увидит их разлетающимися со скоростью 2с, т. е. с удвоенной скоростью света. Но если бы он двигался вместе с одним из этих лучей, то, вычислив относительную скорость в соответствии с приведенной выше формулой, он получил бы

что, конечно, приводит к значению, равному с. Иными словами, он увидел бы другой луч двигающимся от него со скоростью света.
Предположим, что луч света проходит у нас над головой в тот же момент, что и космический корабль, двигающийся в противоположном направлении со скоростью х. В инерциальной системе отсчета
Земли корабль и свет проходят друг мимо друга со скоростью с плюс х. Читатель может доставить себе удовольствие, вычислив значение скорости света, которое получится, если измерять ее в инерциальной системе отсчета, связанной с космическим кораблем. Конечно, в результате должно опять получиться с.
Вне сферы действия специальной теории относительности, имеющей дело только с инерцнальными системами, все же можно говорить о скорости света как о некоем абсолютном пределе. Однако теперь это следует выразить по-иному: нет такого способа, который позволил бы отправить сигнал от одного материального тела к другому со скоростью, превышающей световую. Понятие «сигнал» используется здесь в широком смысле этого слова. Оно включает в себя любой тип причинно-следственной связи, позволяющей переслать какое-либо сообщение: посылка физического объекта, например, или передача любого типа энергии, такой, как энергия звуковых волн, электромагнитных волн, ударных волн в твердом теле и так далее. Нельзя отправить сообщение на Марс со скоростью, превышающей скорость света. Этого нельзя сделать, написав письмо и отправив его в ракете, поскольку, как мы видели ранее, относительная скорость ракеты всегда должна быть меньше скорости света. Если сообщение закодировать и отправить с помощью радио или радара, то оно дойдет со скоростью света. Никакой другой тип энергии не сможет обеспечить более быструю передачу этого кода.
Хотя сигналы не могут быть посланы со скоростью, превышающей скорость света, но можно наблюдать определенные типы движений, которые будут иметь по отношению к наблюдателю скорости больше световой. Представьте себе гигантские ножницы, лезвия которых таковы, что достигают планеты Нептун. Ножницы начинают закрывать с постоянной скоростью. По мере того как это происходит, точка, в которой пересекаются режущие края лезвий, будет двигаться к концам ножниц со все возрастающей скоростью. Представьте, что вы сидите на неподвижном стержне, скрепляющем оба лезвия. По отношению к вашей инерциальной системе отсчета эта точка пересечения лезвий скоро будет удаляться от вас со скоростью, большей скорости света. Конечно, здесь происходит движение не материального тела, а геометрической точки.
Возможно, вам придет в голову такая мысль: предположим, что кольца ножниц находятся на Земле, а точка пересечения лезвий — на Нептуне.
Если вы слегка закрываете ножницы, а затем открываете, повторяя это многократно, то точка пересечения будет ходить вперед — назад. Нельзя ли теперь передать сигналы на Нептун почти мгновенно? Нельзя, поскольку импульс, приводящий в движение лезвия, должен передаваться от молекулы к молекуле, а скорость этого процесса должна быть меньше световой. В общей теории относительности нет абсолютно жестких тел. Иначе вы могли бы просто взять жесткий стержень протяженностью от Земли до Нептуна и передавать сообщения мгновенно, приводя в движение один конец. Не существует способа, который позволил бы использовать гигантские ножницы или любой другой тип так называемых абсолютно твердых объектов для передачи сигнала со скоростью больше скорости света.

Если направить луч прожектора на экран, который достаточно велик и достаточно далеко расположен, то можно, поворачивая прожектор, сделать так, что пятно на экране будет двигаться по нему быстрее света. Здесь опять никакой материальный объект не движется, движение на самом деле является иллюзией. Если прожектор направить в пространство и начать его вращать, то удаленные части луча будут нестись в пространстве со скоростью много больше скорости света. В гл. 5 будет показано, что можно считать Землю невращающейся системой отсчета. С этой точки зрения скорости вращения звезд вокруг Земли будут много больше скорости света. Как отметил один астроном, звезда, удаленная всего лишь на 10 световых лет, имеет круговую скорость относительно Земли, в двадцать тысяч раз превышающую скорость света. При этом геометрическом способе преодоления светового барьера даже нет необходимости следить за звездами.

Вращая волчок, ребенок может сообщить Луне круговую скорость (по отношению к системе координат, связанной с волчком), которая много больше 300 000 км/сек.
В гл. 10 говорится о том, что в соответствии с одной популярной теорией о Вселенной далекие галактики могут удаляться от Земли со скоростью, превышающей скорость света. Ни один из этих примеров не противоречит утверждению, что скорость света является барьером при посылке сигналов от одного материального тела к другому.
Важным следствием специальной теории относительности, которого мы кратко коснемся, является то, что при определенных условиях энергия переходит в массу, а при некоторых других условиях масса переходит в энергию. Физики раньше считали, что полное количество массы во Вселенной никогда не изменяется и что никогда не меняется полное количество энергии. Это выражалось законами «сохранения массы» и «сохранения энергии». Теперь оба эти закона объединены в один простой закон «сохранения массы — энергии».
Когда ракетные двигатели ускоряют космический корабль, часть энергии идет на увеличение релятивистской массы корабля. Когда энергия сообщается кофейнику путем нагревания (при этом ускоряются его молекулы), содержимое кофейника действительно весит немного больше, чем прежде.
Когда кофейник остывает, его масса уменьшается.
Заводя часы, мы сообщаем им энергию, и они в то же время приобретают дополнительно небольшое количество массы. Когда завод кончается, часы теряют эту массу. Эти увеличения и уменьшения маcсы так бесконечно малы, что они никогда не учитываются в обычных физических расчетах. Однако это превращение массы в энергию совсем не ничтожно, когда взрывается водородная бомба!
Взрыв бомбы — это мгновенное превращение в энергию части массы материала бомбы. Энергия, излучаемая Солнцем, имеет подобное происхождение. Вследствие огромной силы тяжести на Солнце газообразный водород внутри него находится под столь большим давлением и нагревается до столь высокой температуры, что атомы водорода сливаются, превращаясь в гелий. В этом процессе некоторое количество массы превращается в энергию.
Формула, выражающая соотношение между массой и энергией, как это известно теперь каждому, такова:
e = mc2
где е — энергия; m — масса; с2 — квадрат скорости света. Эйнштейн получил это выражение из своей специальной теории относительности. Из этой формулы видно, что чрезвычайно малое количество массы способно освободить чудовищное количество энергии. Жизнь на Земле не существовала бы без солнечной энергии, так что в известном смысле жизнь зависит от этой формулы.

Может оказаться, что конец жизни не Земле также будет связан с этой формулой. Не будет преувеличением сказать, что научиться справляться с ужасным фактом, выражаемым этой простой формулой, — самая важная проблема из тех, которые когда-либо стояли перед человечеством.
Однако бомба — это только один наиболее впечатляющий факт из многих фактов, подтверждающих специальную теорию относительности. Экспериментальные доказательства начали накапливаться, едва только высохли чернила на статье Эйнштейна, написанной в 1905 г., и сейчас это одна из наиболее хорошо подтвержденных теорий современной физики. Она каждый день подтверждается в лабораториях учеными-атомниками, работающими с частицами, которые движутся со скоростями, близкими к скорости света. Чем быстрее движутся подобные частицы, тем большая сила необходима, чтобы увеличить их скорость на заданную величину; иными словами, тем больше их релятивистская масса. Именно по этой причине физики продолжают строить все большие и большие машины для ускорения частиц.
Нужны все более сильные поля, чтобы преодолеть массу частиц, растущую по мере того, как их скорость становится ближе и ближе к скорости света.
Электроны теперь могут быть ускорены до скорости в 0,999999999 скорости света. При этом каждый электрон приобретает массу (относительно инерциальной системы отсчета Земли), которая примерно в сорок тысяч раз больше его массы покоя!
Когда какая-либо частица сталкивается со своей античастицей (частицей, имеющей точно такую же структуру, но противоположный электрический заряд), происходит полная и взаимная иу аннигиляция.
Вся масса обеих частиц целиком превращается в энергию излучения. В лаборатории этот процесс пока проводится только с отдельными частицами. Если физикам когда-либо удастся создать антивещество (вещество, построенное из античастиц), то они смогут достичь предела в использовании атомной энергии. Очень небольшое количество антивещества на космическом корабле, поддерживаемое магнитными полями во взвешенном состоянии, можно соединять понемногу с веществом, что обеспечит корабль движущей силой, достаточной, чтобы нести его к звездам.

Специальная теория относительности настолько полно подтверждена экспериментом, что теперь было бы трудно найти физика, который сомневается в правильности этой теории.
Равномерное движение относительно. Но прежде чем можно будет сказать, что всякое движение относительно, нужно преодолеть последнее препятствие: это препятствие — инерция. Что это именно за препятствие и как Эйнштейн преодолел его, описано в гл. 5.






