лас
≤. 
1. «а означенн€м 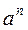 ,
,  ,
,  ,тод≥
,тод≥  . „и завжди можлива ц€ д≥€, €кщо
. „и завжди можлива ц€ д≥€, €кщо  ≥
≥ 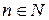 ?
?
Ќ≥, т≥льки тод≥, €кщо  ≥
≥  . “аке обмеженн€ створюЇ незручност≥ при алгебрањчних перетворенн€х, бо оперуючи з буквеними показниками треба, щоразу враховувати, що перетворенн€ частки степен≥в справедливе лише при
. “аке обмеженн€ створюЇ незручност≥ при алгебрањчних перетворенн€х, бо оперуючи з буквеними показниками треба, щоразу враховувати, що перетворенн€ частки степен≥в справедливе лише при  . ÷ю незручн≥сть можна усунути розширивши пон€тт€ про степ≥нь у 8 клас≥, таким чином, щоб властивост≥ степен€ з натуральним показником збереглис€.
. ÷ю незручн≥сть можна усунути розширивши пон€тт€ про степ≥нь у 8 клас≥, таким чином, щоб властивост≥ степен€ з натуральним показником збереглис€.
лас
¬водитьс€ пон€тт€ степен€ з ц≥лим показником у такому пор€дку:
а) ввод€ть степ≥нь з нульовим показником 
б)степ≥нь з ц≥лим в≥дТЇмним показником, щоб правило д≥ленн€ степен≥в одн≥Їњ основи можна було застосувати дл€ випадку, коли 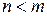 .
.
 ;
;  . јле ви€вилось, що у такому випадку сл≥д обмежити основу
. јле ви€вилось, що у такому випадку сл≥д обмежити основу  ;
;  ; бо вираз
; бо вираз  не маЇ зм≥сту.
не маЇ зм≥сту.
лас
—теп≥нь з рац≥ональним показником. ќзначенн€ степен€ з дробовим показником  маЇ бути таким, щоб властивост≥ степен€ з натуральним показником залишилис€ правильними.
маЇ бути таким, щоб властивост≥ степен€ з натуральним показником залишилис€ правильними.
÷е означенн€ виникло у звТ€зку з бажанн€м узагальнити правило добуванн€ корен€ у випадку, коли показник п≥дкореневого виразу не д≥литьс€ на показник корен€. ѕравило 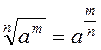 було виведене з припущенн€, що
було виведене з припущенн€, що  ≥
≥ 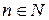 ≥
≥  д≥литьс€ на
д≥литьс€ на  . “епер це правило треба вм≥ти застосовувати ≥ тод≥ коли
. “епер це правило треба вм≥ти застосовувати ≥ тод≥ коли 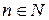 ,
,  . “ут потр≥бно обмежити основу
. “ут потр≥бно обмежити основу  , бо
, бо 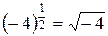 не маЇ зм≥сту.
не маЇ зм≥сту.
ѕропонуЇмо учн€м за допомогою калькул€тора обчислити значенн€ вираз≥в: а)  , б)
, б)  .
.
¬иникаЇ запитанн€: а €к розум≥ти вирази  ,
,  ,
,  .
.
”загальненн€ пон€тт€ степен€
1. —теп≥нь з натуральним показником
 ,
, 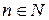

а Ц основа степен€,
n Ц його показник
2. —теп≥нь з ц≥лим показником
 ,
, 
1.  ,
, 
2. 
3.  ,
,  ,
, 
3. —теп≥нь з рац≥ональним показником 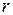 ≥
≥  , де
, де  ,
,  , де
, де  ,
, 
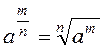 ,
,  ,
,  ,
, 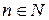 ,
, 
1. якщо  ,
,  то
то 
2. 
| ”загальненн€ пон€тт€ степен€ | ||
| —теп≥нь з натуральним показником | —теп≥нь з ц≥лим показником | —теп≥нь з рац≥ональним показником 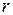 ≥ ≥  , де , де  , ,  , де , де  , , 
|
 , ,  , , 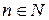 1.
1.  2.
2.  3.
3. 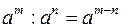 при при  ; ;  4.
4.  5.
5.  6.
6.  , , 
|  , , 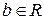 , ,  1.
1.  2.
2.  3.
3.  , при , при  4.
4.  5.
5.  6.
6.  , ,  7.
7.  8. якщо
8. якщо 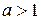 ≥ ≥  , то , то  9. якщо
9. якщо  ≥ ≥  то то

|  , ,  , , 






 , €кщо , €кщо  , , 
 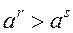 , €кщо , €кщо  , , 
 €кщо €кщо  , , 
 , €кщо , €кщо  , , 
 , €кщо , €кщо  , , 
|
5. ћетодика введенн€ степен€ з ≥ррац≥ональним показником.
ѕ р о п о н у Ї м о у ч н € м:
ќбчислити значенн€ вираз≥в:
а)  ; б)
; б)  ; в)
; в)  , де
, де  Ц ≥ррац≥ональне число.
Ц ≥ррац≥ональне число.
¬иникаЇ потреба ввести означенн€ степен€ з ≥ррац≥ональним показником  , де
, де  - ≥ррац≥ональне число.
- ≥ррац≥ональне число.
¬оно вимагаЇ новоњ конструкц≥њ. ѕри цьому бажано степ≥нь з ≥ррац≥ональним показником означити так, щоб зберегти вс≥ в≥дом≥ властивост≥ степен€ з рац≥ональним показником. “ака спадков≥сть уже мала м≥сце при переход≥ в≥д натурального показника до рац≥онального. ѕроведемо де€к≥ м≥ркуванн€.
–озгл€немо степ≥нь  , де
, де  - ≥ррац≥ональне число, дл€ €кого ≥снують дв≥ посл≥довност≥ рац≥ональних чисел
- ≥ррац≥ональне число, дл€ €кого ≥снують дв≥ посл≥довност≥ рац≥ональних чисел  ≥
≥  вз€т≥ з недостачею ≥ надлишком.
вз€т≥ з недостачею ≥ надлишком.
 : 1; 1,4; 1,41; 1,414; ЕЕ
: 1; 1,4; 1,41; 1,414; ЕЕ
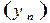 : 2; 1,5; 1,42; 1,415;Е..
: 2; 1,5; 1,42; 1,415;Е..
“обто число 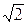 запишемо:
запишемо: 

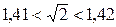

ЕЕЕЕЕЕЕ..

”творимо нов≥ посл≥довност≥ в≥дпов≥дних значенню степен€ числа 3.
|
|
|
 ;
;  ;
;  ; Е..
; Е.. 
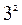 ;
;  ;
;  ;ЕЕ..
;ЕЕ.. 
«а властивост€ми степен€ з рац≥ональним показником випливаЇ, що:
а)  ; б)
; б)  ; в)
; в)  ,
,
де 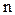 =0, 1, 2, Е..
=0, 1, 2, Е..
можна довести, що ≥снуЇ Їдине число, €ке при будь-€кому 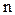 = 0, 1, 2, 3... б≥льше
= 0, 1, 2, 3... б≥льше  ≥ менше
≥ менше 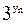 . ÷е число
. ÷е число 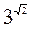 . ≤снуванн€ такого числа можна показати геометрично:
. ≤снуванн€ такого числа можна показати геометрично:

јналог≥чно м≥ркують ≥ дл€ чисел 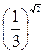 , €ке б≥льше
, €ке б≥льше  ≥ менше
≥ менше  при
при 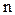 = 0, 1, 2...
= 0, 1, 2...
“аким чином, степ≥нь числа  , з показником
, з показником 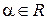 означаЇтьс€ так:
означаЇтьс€ так:
1. якщо  , то
, то  - степ≥нь з ц≥лим показником.
- степ≥нь з ц≥лим показником.
2. якщо  , то
, то 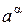 - степ≥нь з рац≥ональним показником.
- степ≥нь з рац≥ональним показником.
3. якщо  , то:
, то:
а) при 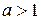 , число
, число 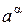 - означаЇ таке число, €ке б≥льше
- означаЇ таке число, €ке б≥льше  ≥ менше
≥ менше 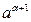 (
( =0, 2, 3, Е.)
=0, 2, 3, Е.) 
б) при  ;
;  (
( =0, 1, 2, Е.)
=0, 1, 2, Е.)
в) при  ;
; 
4. якщо  , то
, то 
Ќаприклад,  .
.
≤снуванн€ ≥ Їдн≥сть числа  доводитьс€ у курс≥ математичного анал≥зу. ¬ластивост≥ степен€ з ≥ррац≥ональним показником приймаютьс€ без доведенн€.
доводитьс€ у курс≥ математичного анал≥зу. ¬ластивост≥ степен€ з ≥ррац≥ональним показником приймаютьс€ без доведенн€.
ƒ≥њ над степен€ми з ≥ррац≥ональним показниками виконуютьс€ за зразками (правилами), €к≥ встановлено дл€ степен≥в з рац≥ональними показниками. —теп≥нь з ≥ррац≥ональним показником збер≥гаЇ вс≥ властивост≥ степен€ з рац≥ональним показником. ” класах з поглибленим вивченн€м математики, де учн≥ знайом≥ з пон€тт€м границ≥ числовоњ посл≥довност≥, можна сформулювати означенн€ з степен€ з ≥ррац≥ональним показником так:
¬прави на закр≥пленн€:
1. ќбчисл≥ть: а) 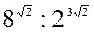 ; б)
; б) 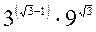 ; в)
; в)  ; г)
; г)  .
.
2. ѕор≥вн€йте числа: а)  ≥
≥  ; б)
; б)  ≥
≥ 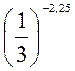
3. —прост≥ть вираз: 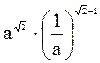 ;
;  ;
;  .
.
4. «а допомогою м≥крокалькул€тора обчисл≥ть з точн≥стю до 0,001 значенн€:
а)  ;
; 
б)  ;
; 
в)  ;
; 
ћаючи результати, знайд≥ть значенн€  з точн≥стю до 0,01.
з точн≥стю до 0,01.
—тепенева функц≥€, властивост≥ та њњ граф≥к.
ќзначенн€: функц≥€ виду  , де х Ц незалежна зм≥нна, а
, де х Ц незалежна зм≥нна, а  називаЇтьс€ степеневою функц≥Їю.
називаЇтьс€ степеневою функц≥Їю.
¬ластивост≥ функц≥њ 
( Ц натуральний показник)
Ц натуральний показник)

1. ќбласть визначенн€
 ,
, 

2. ќбласть значень

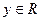
3. 

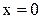
4. 


 ---
--- 
5. ѕарна так н≥
Ќепарна н≥ так
6. ћонотонн≥сть
зростаЇ 

спадаЇ  ------
------
7. Ќайб≥льше та найменше немаЇ
значенн€  немаЇ
немаЇ
√ – ј ‘ ≤ »


 непарне натуральне число:
непарне натуральне число:
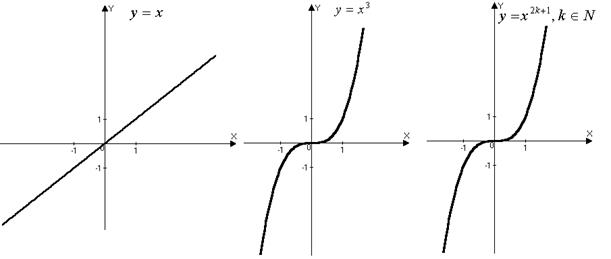
 - непарне в≥дТЇмне число
- непарне в≥дТЇмне число

 - парне в≥дТЇмне число
- парне в≥дТЇмне число

 - нец≥ле додатне число
- нец≥ле додатне число

7. ћетодика введенн€ показниковоњ функц≥њ
а) ћетодичн≥ особливост≥ вивченн€ показниковоњ функц≥њ
Ќа њњ вивченн€ в≥дводитьс€ 20 год (8 год резерв), €к≥ можна спланувати по р≥зному. ќдин з можливих вар≥ант≥в:
1. Ќа вивченн€ теоретичного матер≥алу Ц 4 год. …ого можна провести у вигл€д≥ урок≥в-лекц≥й.
2. Ќа закр≥пленн€ знань, формуванн€ вм≥нь та навичок Ц14 год. “ут можна використати уроки р≥зних вид≥в:
- уроки розвТ€зуванн€ типових (ключових) завдань;
- уроки-практикуми;
- уроки Ц сем≥нари та ≥нш≥ нетрадиц≥йн≥ уроки;
3. ƒл€ тематичного контролю ≥ корекц≥њ знань Ц 2 год.
ќсновна мета вивченн€ теми:
- ввести означенн€ показниковоњ та степеневоњ функц≥њ;
- розгл€нути њх граф≥ки ≥ властивост≥;
- розгл€нути показникових та степеневих р≥вн€нь ≥ нер≥вностей (та њх системи).
¬ результат≥ вивченн€ теми учень повинен знати:
- означенн€ показниковоњ та степеневоњ функц≥њ;
- основн≥ показников≥ та степенев≥ властивост≥;
- означенн€ показникових та степеневих р≥вн€нь.
¬ м ≥ т и:
- будувати еск≥зи, граф≥ки показникових та степеневих функц≥й ≥ УчитатиФ за граф≥ками властивост≥ функц≥й;
- спрощувати показников≥ та степенев≥ вирази;
- розвТ€зувати показников≥ р≥вн€нн€ та нер≥вност≥.
|
|
|
ƒл€ вивченн€ теми можуть бути обран≥:
по€снювально-≥люстративний, репродуктивн≥ методи, у де€ких випадках метод проблемного вивченн€ матер≥алу (наприклад, п≥д час побудови граф≥к≥в функц≥й  ;
; 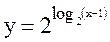 ). ћетоди наукового п≥знанн€: анал≥з; синтез; аналог≥€; пор≥вн€нн€; спостереженн€ узагальненн€. ” класах з поглибленим вивченн€м математики: досл≥дницький, частково-пошуковий, самост≥йн≥ роботи, роботи з п≥дручником, творч≥ самост≥йн≥ роботи.
). ћетоди наукового п≥знанн€: анал≥з; синтез; аналог≥€; пор≥вн€нн€; спостереженн€ узагальненн€. ” класах з поглибленим вивченн€м математики: досл≥дницький, частково-пошуковий, самост≥йн≥ роботи, роботи з п≥дручником, творч≥ самост≥йн≥ роботи.
ѕ≥д час вивченн€ Уѕоказниковоњ та степеневоњ функц≥њФ доц≥льно поЇднати анал≥тичний та граф≥чний методи, подбати, щоб учн≥ добре усв≥домили взаЇмозвТ€зок м≥ж пр€мою та оберненою функц≥€ми. “од≥ на основ≥ властивостей показниковоњ функц≥њ можна вивчити властивост≥ логарифм≥чноњ. “акий п≥дх≥д заощадить час ≥ спри€тиме кращому усв≥домленню властивостей двох взаЇмно обернених функц≥й. ¬≥дпов≥дно до цього доц≥льно розгл€дати матер≥ал теми у так≥й посл≥довност≥:
1. ѕон€тт€ про степ≥нь з ≥ррац≥ональним показником.
2. ќзначенн€ та властивост≥ показниковоњ функц≥њ.
3. ѕоказников≥ р≥вн€нн€ ≥ нер≥вност≥.
4. ѕон€тт€ про логарифми.
5. Ћогарифм≥чна функц≥€, €к обернена до показниковоњ.
6. Ћогарифм≥чн≥ р≥вн€нн€ та нер≥вност≥.
ƒо засоб≥в навчанн€ можна в≥днести перш за все:
- систему вправ, запитань, задач.
÷€ система вправ ≥ задач може виступати €к зас≥б навчанн€ ≥ €к метод навчанн€.
Ќаприклад: чи можна побудувати граф≥к функц≥й  маючи граф≥к функц≥њ
маючи граф≥к функц≥њ  ≥ т.д.
≥ т.д.
- таблиц≥ з граф≥ками, кольорова крейда, кадескоп, ще краще компТютер, калькул€тор дл€ обчисленн€ степен≥в з рац≥ональним показником виду  ,
, 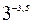 ,
,  ;
;
-дидактичний роздатковий матер≥ал, р≥зних р≥вн≥в складност≥.
ѕ≥д час вивченн€ теми можна використати р≥зн≥ форми навчальноњ д≥€льност≥ учн≥в, а саме: фронтальну, групову, парну, ≥ндив≥дуальну. “аким чином, вчитель враховуючи зм≥ст навчального матер≥алу, математичну п≥дготовку учн≥в, та своњ особист≥ €кост≥ повинен вибрати найб≥льш рац≥ональн≥ методи, форми та засоби навчанн€, щоб забезпечити виконанн€ мети навчанн€.
б) ћотивац≥€ вивченн€ показниковоњ функц≥њ
—ьогодн≥ багато говор€ть про ≥нформац≥йний багажник. —тверджують, що к≥льк≥сть ≥нформац≥њ подвоюЇтьс€ кожн≥ дес€ть рок≥в, зобразимо це у вигл€д≥ граф≥ка де€коњ функц≥њ. ¬≥зьмемо обс€г ≥нформац≥њ у де€кий початковий р≥к за 1. ”дв≥ч≥ б≥льший в≥др≥зок поставимо над одиничною оц≥нкою, вважаючи, що оц≥нка в≥дповнюЇтьс€ першому дес€тку рок≥в. ”дв≥ч≥ б≥льший в≥др≥зок в≥дпов≥даЇ другому дес€тку рок≥в ≥ т.д.
ќбран≥ нами значенн€ аргументу Ї елементами арифметичноњ прогрес≥њ 1, 2, 3,....ј значенн€ функц≥њ зростають за законом геометричноњ прогрес≥њ 2, 4, 8,... ѕобудуЇмо граф≥к функц≥њ.
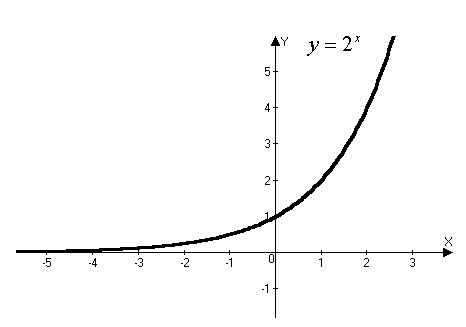
ѕеред нами граф≥к показниковоњ функц≥њ. √оловна особлив≥сть ц≥Їњ функц≥њ Ц крутизна. ѕоказников≥ функц≥€ зустр≥чаЇтьс€ в опис≥ процес≥в, у €ких швидк≥сть зм≥ни величини пропорц≥йна до самоњ величини. «а таким правилом розмножуЇтьс€ все живе. «а законом експоненц≥ального зростанн€ зб≥льшуЇтьс€ колон≥€ м≥кроб≥в у чашц≥ ѕетр≥. «а таким законом плодилис€ крол≥, €к≥ за короткий терм≥н заполонили јвстрал≥ю. ѕрикладом показникового спаданн€ Ї х≥д х≥м≥чноњ реакц≥њ. Ўвидк≥сть х≥м≥чноњ реакц≥њ пропорц≥йна до к≥лькост≥ речовин, що реагують. Ўвидк≥сть рад≥оактивного розпаду пропорц≥йна до к≥лькост≥ атом≥в, що не розпалис€.
«адача
” де€к≥й культур≥ через два дн≥ утворюЇтьс€ 370000 бактер≥й, через 5 дн≥в Ц 5310100. —к≥льки њх було спочатку, через 1 день, через 3 дн≥.

370 000 = 
5 310 000 = 


в) ƒе€к≥ задач≥, що привод€ть до пон€тт€ показниковоњ функц≥њ
—початку розгл€немо конкретн≥ приклади функц≥ональних залежностей, €к≥ ≥люструють використанн€ показниковоњ функц≥њ дл€ опису р≥зних €вищ природи.
«адача. ƒержавн≥ ощадкаси нараховують вкладникам по 9% за терм≥н вкладанн€. ¬кладник 1.01.98р. поклав у ощадкасу 500 гривень. яку суму становитиме його вклад через 10 рок≥в?
–озвТ€занн€
–озвТ€жемо цю задачу у загальному вигл€д≥. Ќехай вклад на 1.01.98 становить а гривень, тод≥ 1.01.1999р. каса нараховуЇ 9%=0,009 в≥д суми а гривень ≥ його вклад становитиме (а+0,09а) гривень або 1,09а гривень.
|
|
|
Ќа 1.01.2000р. 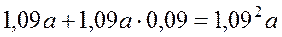 гривень. ћ≥ркуючи так ≥ дальше, знайдемо, що розм≥ри вклад≥в утворюють геометричну прогрес≥ю
гривень. ћ≥ркуючи так ≥ дальше, знайдемо, що розм≥ри вклад≥в утворюють геометричну прогрес≥ю 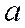 ,
,  ,
,  ,
,  Е.. ≥з знаменником
Е.. ≥з знаменником  .
.
„ерез  повних рок≥в вклад становить
повних рок≥в вклад становить 
Ќаведемо конкретн≥ приклади функц≥ональних залежностей (про зм≥ну атмосферного тиску)
ѕриклад 1
јтмосферний тиск зм≥нитьс€ в залежност≥ в≥д висоти  над р≥внем мор€ за законом
над р≥внем мор€ за законом  , де
, де 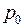 - атмосферний тиск на р≥вн≥ мор€ (7600), а Ц де€ка стала.
- атмосферний тиск на р≥вн≥ мор€ (7600), а Ц де€ка стала.
ѕриклад 2
ƒерево росте так, що к≥льк≥сть деревини зб≥льшуЇтьс€ з часом за законом  , де ћ- к≥льк≥сть деревини у даний момент, (
, де ћ- к≥льк≥сть деревини у даний момент, ( ).
).
ћ Ц початкова к≥льк≥сть деревини,  - час (у роках), €кий в≥дл≥чують з моменту
- час (у роках), €кий в≥дл≥чують з моменту  ,
, 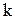 - де€ка стала. «а ск≥льки рок≥в обТЇм деревини зб≥льшитьс€ в
- де€ка стала. «а ск≥льки рок≥в обТЇм деревини зб≥льшитьс€ в  раз≥в?
раз≥в?
–озвТ€занн€
якщо в даний момент 
 , то под≥ливши обидв≥ частини р≥вн€нн€
, то под≥ливши обидв≥ частини р≥вн€нн€  на
на  д≥станемо
д≥станемо  ,
, 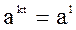 ,
,  ,
, 
ќбТЇм деревини зб≥льшитьс€ в а раз≥в через  рок≥в.
рок≥в.
ѕриклад 3
–озмноженн€ бактер≥й у певному середовищ≥ в≥дбуваютьс€ так, що њх число  зм≥нюЇтьс€ з часом за законом
зм≥нюЇтьс€ з часом за законом  , де
, де  - початкове число бактер≥й при
- початкове число бактер≥й при  ,
,  ≥
≥ 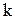 - де€к≥ стал≥.
- де€к≥ стал≥.
” наведених прикладах дл€ обчисленн€ кожного значенн€ функц≥њ певне число а, одне ≥ те саме на прот€з≥ всього процесу доводитьс€ п≥дносити до де€кого степен€. Ќайпрост≥шим випадком ц≥Їњ залежност≥ Ї функц≥€  , де а Ц додатне д≥йсне число, х Ц залежна зм≥нна, що набуваЇ будь-€ких д≥йсних значень. ќчевидно, вона маЇ свою назву. ќск≥льки показником Ї зм≥нна величина, то функц≥€ називаЇтьс€ показниковою.
, де а Ц додатне д≥йсне число, х Ц залежна зм≥нна, що набуваЇ будь-€ких д≥йсних значень. ќчевидно, вона маЇ свою назву. ќск≥льки показником Ї зм≥нна величина, то функц≥€ називаЇтьс€ показниковою. 
1. ѕри  , а х Ц рац≥ональне, знаменник, €кого парне число, вираз
, а х Ц рац≥ональне, знаменник, €кого парне число, вираз  не маЇ смислу.
не маЇ смислу.
Ќаприклад:  ,
, 
 у множинах д≥йсних чисел не маЇ смислу.
у множинах д≥йсних чисел не маЇ смислу.
2.  ,
,  , степ≥нь
, степ≥нь  ≥снуЇ.
≥снуЇ.
јле при  ,
,  , степ≥нь
, степ≥нь  - не маЇ смислу.
- не маЇ смислу.
Ќаприклад:  ;
; 
3. ѕри  ,
,  степ≥нь
степ≥нь  або
або 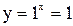 , така функц≥€ ≥снуЇ, в≥дноситьс€ до л≥н≥йних. ¬она Ї сталою ≥ не становить ≥нтересу. “ому значенн€
, така функц≥€ ≥снуЇ, в≥дноситьс€ до л≥н≥йних. ¬она Ї сталою ≥ не становить ≥нтересу. “ому значенн€  виключають у розгл€ду.
виключають у розгл€ду.
“аким чином, формулюЇмо означенн€ показниковоњ функц≥њ. ‘ункц≥€, €ку можна задати р≥вн≥стю 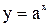 , де
, де  ,
,  ,
,  називаЇтьс€ показниковою.
називаЇтьс€ показниковою.
г) ¬ластивост≥ показниковоњ функц≥њ
” шк≥льн≥й практиц≥ ≥снуЇ 2 п≥дходи до вивченн€ властивостей показниковоњ функц≥њ.
a. —початку довод€ть анал≥тично вс≥ властивост≥, а пот≥м розгл€даЇтьс€ функц≥€ при конкретному значенн≥ а ≥ будуЇтьс€ граф≥к. “акий п≥дх≥д був обраний у п≥дручнику алгебри исельова. ¬≥н ви€вивс€ важким дл€ сприйманн€ учн€ми, тобто це Ї дедуктивний метод.
b. «а точками (за допомогою заздалег≥дь складеноњ на дошц≥ таблиц≥, або фабричноњ), будуютьс€ граф≥ки певних показникових функц≥й.
Ќаприклад: 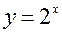 ;
;  ;
; 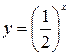 ;
;  ≥ за граф≥ком зТ€совують властивост≥ функц≥њ
≥ за граф≥ком зТ€совують властивост≥ функц≥њ  при
при  та
та 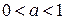 , а пот≥м ц≥ властивост≥ довод€ть анал≥тично. “акий п≥дх≥д прийн€тий у б≥льшост≥ п≥дручник≥в та пос≥бник≥в у тому числ≥ ≥ д≥ючому п≥дручнику з алгебри та початк≥в анал≥зу. ”читель вказуЇ, що при вивченн≥ властивостей показниковоњ функц≥њ заслуговують на увагу два ≥стотних випадки:
, а пот≥м ц≥ властивост≥ довод€ть анал≥тично. “акий п≥дх≥д прийн€тий у б≥льшост≥ п≥дручник≥в та пос≥бник≥в у тому числ≥ ≥ д≥ючому п≥дручнику з алгебри та початк≥в анал≥зу. ”читель вказуЇ, що при вивченн≥ властивостей показниковоњ функц≥њ заслуговують на увагу два ≥стотних випадки:
1. ќснова а Ї неправильним дробом тобто 
2. ќснова а Ц правильний др≥б 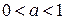
ѕри цьому п≥дкреслюЇтьс€ уже в≥доме твердженн€.
1. ƒодатний степ≥нь неправильного дробу б≥льший в≥д 1;
Ќаприклад  .
.
¬≥дТЇмний степ≥нь неправильного дробу менший в≥д 1 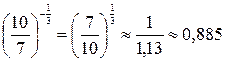
ƒал≥ будуЇмо граф≥к функц≥њ  .
. 


| -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0,5 | 1,5 | |||
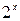
| 0,125 | 0,177 | 0,25 | 0,354 | 0,5 | 0,707 | 1,414 | 2,828 |

—кладаЇмо таблицю значень аргументу ≥ в≥дпов≥дних значень функц≥й:



| -4 | -3 | -2 | -1 | ||||
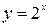
| 
| 
| 
| 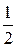
|

ЅудуЇмо граф≥ки, сполучаЇмо плавною л≥н≥Їю.
–озгл€немо функц≥ю  . —кладаЇмо аналог≥чно таблицю:
. —кладаЇмо аналог≥чно таблицю:
|
|
|

| -3 | -2 | -1 | ||||

| 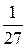
| 
| 
|

ЅудуЇмо граф≥к функц≥њ 

| -4 | -3 | -2 | -1 | |||||

| 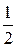
| 
| 
| 
|

–озгл€даючи граф≥ки функц≥й ви€снимо, що сп≥льного у граф≥к≥в функц≥й  ≥
≥ 
1) ќбласть визначенн€ обох функц≥й Ї 
2) ќбидв≥ функц≥њ додатн≥ при будь-€кому х.
ѕри х=0 обидв≥ функц≥њ набувають значень, що дор≥внюЇ 1.
ƒал≥ будуЇмо граф≥к функц≥й  ≥
≥  в одн≥й систем≥ координат ≥ пор≥внюЇмо њх властивост≥:
в одн≥й систем≥ координат ≥ пор≥внюЇмо њх властивост≥:

1) √раф≥ки розм≥щен≥ симетрично в≥дносно ос≥ ординат.
2)  - зростаЇ,
- зростаЇ,  - спадаЇ.
- спадаЇ.
3) ѕри 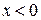
 набуваЇ значень
набуваЇ значень 


 при
при 
 , а при
, а при 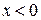
 .
.
¬ластивост≥ функц≥њ  при
при  ≥ при
≥ при 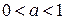 суттЇво в≥др≥зн€ютьс€.
суттЇво в≥др≥зн€ютьс€.
“ому спочатку розгл€немо загальн≥ властивост≥ показниковоњ функц≥њ, а пот≥м окремо дл€  ≥
≥ 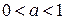 .
.
1. ќбласть визначенн€  Ї множина
Ї множина  , бо при
, бо при  ,
, 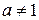 вираз
вираз  - визначений дл€ будь-€кого
- визначений дл€ будь-€кого  .
.
2.ѕоказникова функц≥€ при будь-€кому  додатна, тобто
додатна, тобто 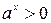 . —правд≥
. —правд≥  може дор≥внювати нулю лише тод≥, коли
може дор≥внювати нулю лише тод≥, коли  . јле ми домовл€Їмос€, що
. јле ми домовл€Їмос€, що  .
.
‘ункц≥€  може бути в≥дТЇмною лише при
може бути в≥дТЇмною лише при  (
( ). јле ми домовимос€ розгл€дати показников≥ функц≥ю лише при
). јле ми домовимос€ розгл€дати показников≥ функц≥ю лише при  . ј при п≥днесенн≥ додатного числа до степен€
. ј при п≥днесенн≥ додатного числа до степен€  , де
, де  завжди матимемо додатне число. ўоб переконатис€ в цьому розгл€немо чотири випадки:
завжди матимемо додатне число. ўоб переконатис€ в цьому розгл€немо чотири випадки:
а) Ќехай  , де
, де  . “од≥
. “од≥ 
€к добуток додатних чисел.
б)якщо х Ц рац≥ональне додатне число, тобто 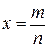 , де
, де  - нескоротний др≥б
- нескоротний др≥б  ≥
≥ 
 , то
, то  .
.
јле  (умова ≥снуванн€ корен€
(умова ≥снуванн€ корен€  - го степен€, або значенн€ степен€ з додатним рац≥ональним показником, тому
- го степен€, або значенн€ степен€ з додатним рац≥ональним показником, тому  .
.
в) Ќехай  Ц додатне ≥ррац≥ональне додатне число. ѕозначимо через
Ц додатне ≥ррац≥ональне додатне число. ѕозначимо через  ≥
≥  наближен≥ (рац≥ональн≥ додатн≥ значенн€ з недостачею ≥ надлишком. “од≥ значенн€
наближен≥ (рац≥ональн≥ додатн≥ значенн€ з недостачею ≥ надлишком. “од≥ значенн€  м≥ститьс€ м≥ж двома додатними числами
м≥ститьс€ м≥ж двома додатними числами  ≥
≥ 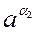 ,
, 



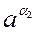 , отже
, отже 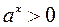 .
.
г) якщо х Ц де€ке в≥дТЇмне число:
наприклад:  , то
, то  . јле у пункт≥ показано, що при будь-€кому додатному рац≥ональному
. јле у пункт≥ показано, що при будь-€кому додатному рац≥ональному  . ќтже,
. ќтже, 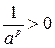 , а значить
, а значить 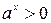 , отже, граф≥к показниковоњ функц≥њ завжди лежить над в≥ссю абсцис ≥ не перетинаЇ њњ (
, отже, граф≥к показниковоњ функц≥њ завжди лежить над в≥ссю абсцис ≥ не перетинаЇ њњ ( ).
).
30. ѕри х = 0 показникова функц≥€  . ÷е випливаЇ з того, що будь-€ке число в≥дм≥нне в≥д нул€ у нульовому степен≥ дор≥внюЇ одиниц≥. ј ми домовимос€ розгл€дати функц≥ю дл€
. ÷е випливаЇ з того, що будь-€ке число в≥дм≥нне в≥д нул€ у нульовому степен≥ дор≥внюЇ одиниц≥. ј ми домовимос€ розгл€дати функц≥ю дл€  . «в≥дси висновок, що граф≥к функц≥њ проходить через точку (0; 1) тобто перетворюЇ в≥сь ординат на в≥дстан≥ одиниц≥ в≥д початку координат.
. «в≥дси висновок, що граф≥к функц≥њ проходить через точку (0; 1) тобто перетворюЇ в≥сь ординат на в≥дстан≥ одиниц≥ в≥д початку координат.
÷≥ три властивост≥ сп≥льн≥ дл€ будь-€ких показникових функц≥й.
40. ѕри  ,
,  , €кщо
, €кщо  ≥
≥
 , €кщо
, €кщо 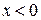 ;
;
ѕри  ,
,  , €кщо
, €кщо 
 , €кщо
, €кщо 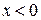 .
.
ƒоведенн€
1. ƒоведемо цю властив≥сть дл€  .
.
а) якщо  ,
,  , тод≥
, тод≥ 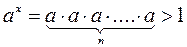
б) якщо 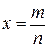 (
( ≥
≥  ), тод≥
), тод≥

«а доведеним вище  ;
;
“од≥ 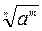
 , тобто
, тобто 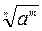
 , а значить
, а значить  .
.
в)  Ц ≥ррац≥ональне додатне число.
Ц ≥ррац≥ональне додатне число.
«а означенн€м степен€ з додатного ≥ррац≥онального показника при  маЇмо
маЇмо  ,
,  , а значить
, а значить  .
.
г) якщо  Ц будь-€ке в≥дТЇмне д≥йсне число.
Ц будь-€ке в≥дТЇмне д≥йсне число.
Ќехай 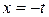 , де
, де  .
. 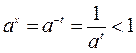 бо за доведенн€м
бо за доведенн€м  .
.
50. ѕри  функц≥€
функц≥€  монотонно зростаЇ,
монотонно зростаЇ, 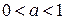 - монотонно спадаЇ.
- монотонно спадаЇ.
ƒоведенн€
1)  . ¬≥зьмемо два значенн€
. ¬≥зьмемо два значенн€  ≥
≥  при чому
при чому  .
.
ƒоведемо, що 
ѕор≥вн€Їмо  ≥
≥  дл€ цього застосовуЇмо р≥зницю
дл€ цього застосовуЇмо р≥зницю  .
.
а) «а властив≥стю 10  .
.
б) «а умови  тому
тому  , а значить
, а значить 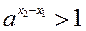 за властив≥стю 20.
за властив≥стю 20.
ќтже,  , а значить добуток
, а значить добуток  тобто
тобто 
ѕроектуЇмо на екран малюнок на €кому зображен≥ граф≥ки показниковоњ функц≥й при р≥зних параметрах

«ауважимо, що дл€ вс≥х функц≥й граф≥ки €ких зображено на малюнку Ї сп≥льн≥ властивост≥.
1) 

2) 
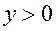
3) 

д ) ¬прави дл€ закр≥пленн€ властивостей показниковоњ функц≥њ
1. якщо граф≥ки функц≥й  ≥
≥  симетричн≥ в≥дносно ос≥ ординат, то €ке сп≥вв≥дношенн€ ≥снуЇ м≥ж
симетричн≥ в≥дносно ос≥ ординат, то €ке сп≥вв≥дношенн€ ≥снуЇ м≥ж  ≥
≥  ?
?
2. „и мають сп≥льну точку граф≥ки  ≥
≥  ?
?
3. у €к≥й точц≥ перетинаютьс€ граф≥к функц≥њ 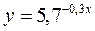 з в≥ссю ординат?
з в≥ссю ординат?
4. як≥ процеси в галуз≥ техн≥ки та природознавства виражають за допомогою показниковоњ функц≥њ?
5. як≥ з функц≥њ  ;
;  ;
;  ;
;  ;
;  Ц Ї показниковими.?
Ц Ї показниковими.?
6. «а €ких умов  ;
;  ?
?
7. яка особлив≥сть розм≥щенн€ граф≥к≥в функц≥й  ;
;  ;
;  ;
;  ?
?
8. ¬≥домо, що  . ўо б≥льше
. ўо б≥льше  чи
чи  при
при  ?
?
9. ѕор≥вн€йте  ≥
≥  , €кщо в≥домо, що
, €кщо в≥домо, що  ≥
≥  .
.
10. „и правильно Ї нер≥вн≥сть  при
при






