Знайти лінію, що проходить через точку М0, якщо відрізок довільної її нормалі, що міститься між осями координат, ділиться точкою лінії у відношенні а:b (рахуючи від осі Oy).
8.6 М0 (1,1), а: b =1:2.
8.7 М0 (-2,3), а: b =1:3.
8.8 М0 (0,1), а: b =2:3.
8.9 М0 (1,0), а: b =3:2.
8.10 М0 (2,-1), а: b =3:1.
Знайти лінію, що проходить через точку М0, якщо відрізок довільної її дотичної між точкою дотику та віссю Oy ділиться в точці перетину з віссю абсцис у відношенні а:b (рахуючи від осі Oy).
8.11 М0 (2,-1), а: b =1:1.
8.12 М0 (1,2), а: b =2:1.
8.13 М0 (-1,1), а: b =3:1.
8.14 М0 (2,1), а: b =1:2.
8.15 М0 (1,-1), а: b =1:3.
Знайти лінію, що проходить через точку М0, якщо відрізок довільної її дотичної, що міститься між осями координат, ділиться в точці дотику у відношенні а:b (рахуючи від осі Oy).
8.16 М0 (1,2), а: b =1:1.
8.17 М0 (2,1), а: b =1:2.
8.18 М0 (1,3), а: b =2:1.
8.19 М0 (2,-3), а: b =3:1.
8.20 М0 (3,-1), а: b =3:2.
Знайти лінію, що проходить через точку М0, яка має властивість, що в довільній її точці М дотичний вектор MN із кінцем на осі Ox має проекцію на вісь Ox, що обернено пропорційна абсцисі точки М. Коефіцієнт пропорційності дорівнює а.
8.21 М0 (1, e), а = -1/2.
8.22 М0 (2, e), а = -2.
8.23 М0 (-1,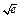 
), а = -1.
8.24 М0 (2,1/ e), а = 2.
8.25 М0 (1,1/ e2), а = 1/4.
Знайти лінію, що проходить через точку М0, яка має властивість, що в довільній її точці М дотичний вектор MN із кінцем на осі Oy має проекцію на вісь Oy, що дорівнює а.
8.26 М0 (1,2), а = -1.
8.27 М0 (1,4), а = 2.
8.28 М0 (1,5), а = -2.
8.29 М0 (1,3), а = -4.
8.30 М0 (1,6), а = 3.
Завдання 11. Знайти загальний розв’язок лінійної неоднорідної системи диференціальних рівнянь:
11.1 
11.2 
11.3 
11.4 
11.5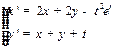 
11.6 
11.7 
11.8 
11.9 
11.10 
11.11 
11.12 
11.13 
11.14 
11.15 
11.16 
11.17 
11.18 
11.19 
11.20 
11.21 
11.22 
11.23 
11.24 
11.25 
11.26 
11.27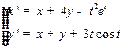 
11.28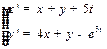 
11.29 
11.30 
