÷ель работы: изучить способы кодировани€ сигнала с помощью неортогональных функций.
«адачи работы:
- »сследовать принципы разделени€ каналов с помощью кодировани€ неортогональными функци€ми.
- ѕровести кодирование информации с помощью неортогональных функций.
ќбщие сведени€
Ќеортогональные (асинхронные) псевдослучайные функции могут быть сгенерированы с применением сдвиговых регистров, сумматоров (сложение по модулю 2) и контуров обратной св€зи. –ис. 4.1 иллюстрирует такой принцип.

–ис. 4.1. √енератор последовательности максимальной длины (m Ц последовательности)
ћаксимальна€ длина последовательности определ€етс€ длиной регистра и конфигурацией цепи обратной св€зи (на рис. 4.1 цепи обратной св€зи обозначены  ,
,  ). „асто эта конфигураци€ цепи обратной св€зи задаетс€ в виде образующего полинома. ƒл€ приведенного рисунка
). „асто эта конфигураци€ цепи обратной св€зи задаетс€ в виде образующего полинома. ƒл€ приведенного рисунка 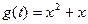 . –егистр длиной
. –егистр длиной  битов может порождать свыше
битов может порождать свыше  различных комбинаций нулей и единиц. “ак как цепь обратной св€зи выполн€ет линейные операции, то если все регистры будут иметь нулевое значение, выход цепи обратной св€зи также будет нулевой. ѕоэтому, если установить все разр€ды на нуль, то цепь обратной св€зи будет всегда давать нулевой выход дл€ всех последующих тактовых циклов, так что необходимо исключить эту комбинацию из возможных последовательностей. “аким образом, максимальна€ длина любой последовательности равна
различных комбинаций нулей и единиц. “ак как цепь обратной св€зи выполн€ет линейные операции, то если все регистры будут иметь нулевое значение, выход цепи обратной св€зи также будет нулевой. ѕоэтому, если установить все разр€ды на нуль, то цепь обратной св€зи будет всегда давать нулевой выход дл€ всех последующих тактовых циклов, так что необходимо исключить эту комбинацию из возможных последовательностей. “аким образом, максимальна€ длина любой последовательности равна  . √енерируемые последовательности называютс€ последовательност€ми максимальной длины, или m-последовательност€ми. ќсновное свойство таких последовательностей: автокоррел€ционна€ функци€ m-последовательности имеет пик при нулевом сдвиге и малый уровень боковых выбросов в остальных случа€х. Ёто позвол€ет более четко выдел€ть каналы. онфигурации обратной св€зи дл€ m-последовательности сведены в таблицы и могут быть найдены в литературе.
. √енерируемые последовательности называютс€ последовательност€ми максимальной длины, или m-последовательност€ми. ќсновное свойство таких последовательностей: автокоррел€ционна€ функци€ m-последовательности имеет пик при нулевом сдвиге и малый уровень боковых выбросов в остальных случа€х. Ёто позвол€ет более четко выдел€ть каналы. онфигурации обратной св€зи дл€ m-последовательности сведены в таблицы и могут быть найдены в литературе.
ѕри модул€ции псевдослучайной последовательностью поступают аналогично модул€ции ортогональными функци€ми ”олша: замен€ют 0 на -1 и умножают все разр€ды последовательности на значение информационного бита. ѕосле этого производитс€ очередной сдвиг и умножение следующего информационного бита на новую последовательность и т. д. —игналы разных каналов суммируютс€. ѕри приеме сообщени€ на коррел€торе происходит перемножение с этой же псевдослучайной последовательностью(см. рис 3.1), интегрирование, сравнение с пороговым значением дл€ прин€ти€ решени€.
’од работы.
- Ќа основании полинома нарисовать схему генератора псевдослучайной последовательности.
| ѕосл.цифра номера по журналу | ќбразующий полином |

| |
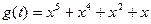
| |

| |

| |

| |

| |

| |

| |

| |

|
- ¬ыполнить кодирование одного канала с 4-битной исходной информацией (последн€€ цифра номера по журналу) с базой сигнала(отношением длительности бита информационного сигнала к длительности бита расшир€ющего сигнала) равной длине регистра и начальным значением регистра в котором чередуютс€ 0 и 1.
|
|
|
ќглавление
Ћабораторна€ работа є1 »сследовать емкость €чейки системы сотовой св€зи. 3
ЋјЅќ–ј“ќ–Ќјя –јЅќ“ј є2 »——Ћ≈ƒќ¬јЌ»≈ Ћј—“≈–ј —»—“≈ћџ —ќ“ќ¬ќ… —¬я«» 6
Ћабораторна€ работа є3 ћЌќ√ќ—“јЌ÷»ќЌЌџ… ƒќ—“”ѕ — ќƒќ¬џћ –ј«ƒ≈Ћ≈Ќ»≈ћ Ќј ќ—Ќќ¬≈ ќ–“ќ√ќЌјЋ№Ќџ’ ‘”Ќ ÷»… ”ќЋЎј. 9
Ћабораторна€ работа є4 ћЌќ√ќ—“јЌ÷»ќЌЌџ… ƒќ—“”ѕ — ќƒќ¬џћ –ј«ƒ≈Ћ≈Ќ»≈ћ Ќј ќ—Ќќ¬≈ Ќ≈ќ–“ќ√ќЌјЋ№Ќџ’ ѕ—≈¬ƒќ—Ћ”„ј…Ќџ’ ‘”Ќ ÷»…. 14






