Сечение кривых поверхностей плоскостью
В сечении поверхности цилиндра вращения плоскостью может получиться:
окружность, если секущая плоскость перпендикулярна к оси цилиндра;
эллипс, если секущая плоскость наклонена к оси цилиндра;
две образующие, если секущая плоскость параллельна оси цилиндра.
На рисунке рассмотрен пример пересечения поверхности цилиндра вращения ω двумя плоскостями. Плоскость α (профильная плоскость уровня) параллельна оси цилиндра и пересекает его поверхность по двум образующим n и m. Плоскость β (фронтально-проецирующая) пересекает поверхность цилиндра по эллипсу l. Его фронтальная и горизонтальная проекции располагаются на вырожденных проекциях секущей плоскости β и цилиндра ω. l’ ≡ ω’; l’’ ≡ β’’.
Профильная проекция эллипса - сечения l’’’ построена по принадлежности точек поверхности цилиндра. Построение начато с выделения опорных точек 1, 2, 21, 4, 41 и дополнено построением промежуточных точек 3, 31 и др.
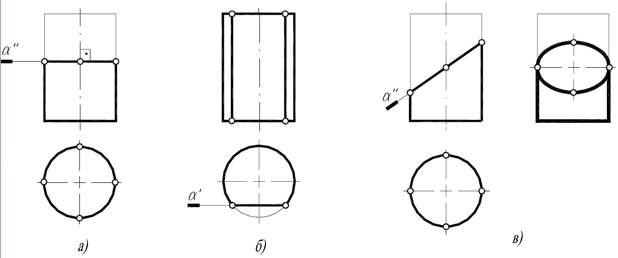
Примеры сечения поверхности цилиндра вращения плоскостью:
а) окружность; б) две прямые; в) эллипс

Пересечение поверхности цилиндра вращения плоскостями α и β
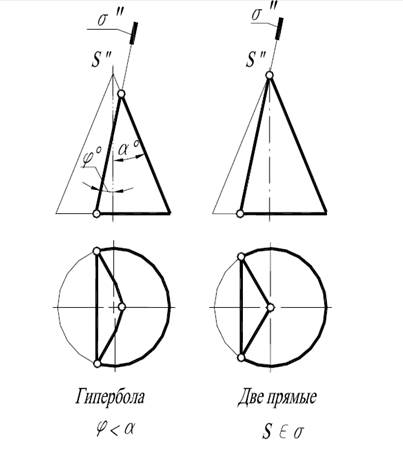
В зависимости от положения секущей плоскости на поверхности конуса вращения получают различные кривые 2-го порядка - окружность, эллипс, параболу или гиперболу. Плоскость, проходящая через вершину конуса, пересекает его поверхность по двум прямым - образующим конуса.