Измерение информации в технике

Для измерения объёма памяти Э.В.М. байт – слишком мелкая единица, практичнее использовать производные единицы – килобайт (1 килобайт = 2 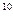байтам = 1024 байтам), мегабайт (1 мегабайт = 2 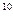килобайтам) и гигабайт (1 гигабайт = 2 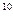мегабайтам). Эти производные единицы обозначаются Кб, Мб и Гб соответственно.

Следует отметить в завершении этого пункта, что количество информации при объёмном способе её измерения более справедливо называть информационным объёмом сообщения, поскольку к информативности сообщения данная величина может не иметь никакого отношения. Действительно, предположим, что в начале передачи информации появился шум, который полностью “забил” полезный сигнал, так что последний выделить невозможно, или изначально передаче подверглась бессмысленная мешанина из символов, или передавался текст, не ставящий получателя ни в какое иное состояние, кроме тупикового (скажем, “Грузите апельсины бочками”), или текст, который получатель знает наизусть (например, таблица умножения). Смысловое содержание сообщения при объёмном способе измерения информации не играет никакой роли, поэтому термин “количество информации” в данном случае мало уместен[4] и, действительно разумнее говорить о (потенциальном) информационном объёме сообщения, его информационной длине, а не о количестве информации.

4.3. Измерение информации в теории информации (информация как снятая неопределённость).

Раздел информатики (теории информации), изучающий методы измерения информации, называется информметрией. В данном разделе под количеством информации понимается числовая величина, адекватно характеризующая актуализируемую информацию по разнообразию, сложности, структурированности, определённости, выбору (вероятности) состояний отображаемой системы.

Если рассматривается система, которая может принимать одно из n возможных состояний, то актуальна задача оценки такого выбора, исхода. Такой оценкой может служить мера информации (или события). Мера – это некоторая непрерывная действительная неотрицательная функция, определённая на множестве событий и являющаяся аддитивной, т.е. мера конечного объединения событий (множеств) равна сумме мер каждого события.

1. Мера Р. Хартли. Пусть имеется N состояний системы S или N опытов с различными, равновозможными последовательными состояниями системы. Если каждое состояние системы закодировать, например, двоичными кодами определённой длины d, то эту длину необходимо выбрать так, чтобы число всех различных комбинаций было не меньше, чем N. Наименьшее число, при котором это возможно, или мера разнообразия множества состояний системы (другими словами, мера неопределённости системы), задаётся формулой Р. Хартли: 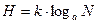, где a – основание системы меры, k – коэффициент пропорциональности (масштабирования, в зависимости от выбранной единицы измерения меры).

Почему неопределённость характеризуется не самой величиной N, а её логарифмом? Чтобы ответить на этот вопрос рассмотрим конкретные ситуации.

Пусть наш опыт состоит в бросании двух кубиков одновременно. Нетрудно подсчитать, что для двух кубиков получается 36 различных равновероятных комбинаций выпадения очков; все они представлены в следующей таблице (первое число в паре указывает количество очков, выпавших на первом кубике, второе число – количество очков, выпавших на втором):

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

Число исходов по сравнению с опытом с одним кубиком (где число исходов 6) увеличилось в 6 раз. Следует ли при этом считать, что неопределённость возросла в 6раз?

Если мы будем подбрасывать монету, то число исходов равно 2. Если подбрасывать две монеты, число исходов становится равным 4, т.е. возросло в 2 раза. А ведь схема опыта одна и та же: вместо одного предмета подбрасываются два. Поэтому естественно считать, что величина неопределённости в этом случае удваивается независимо от того, сколько исходов имеет опыт с одним предметом. И вообще, если проводится два независимых опыта и в одном из них неопределённость исхода равна H 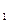, а в другом – H 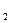, то договариваются считать, что при одновременном проведении этих двух опытов неопределённость равна сумме неопределённостей в каждом из них. Но легко подсчитать, что если в одном опыте было k равновероятных исходов, а в другом m, то число исходов при их одновременном проведении равно k∙m. Всё вышесказанное означает, что H(k∙m)=H(k) + H(m). Кроме этого, очевидно, что при k=1 H=0 (при единственном исходе неопределённость отсутствует).

Хорошо известно, что такими свойствами обладает логарифмическая функция. Поэтому полагают, что H(k)=log(k)[5]. Основание логарифма принципиальной роли не играет. Обычно его выбирают равным 2, поскольку за единицу измерения неопределённости принимают неопределённость, имеющуюся при наступлении одного из двух равновероятных событий. Если за единицу неопределённости взять неопределённость, присутствующую при проведении опыта с десятью равновероятными исходами, то получился бы десятичный логарифм (чтобы log(10)=1). На самом деле выбор основания логарифма принципиального значения не имеет, поскольку переход к другому основанию, как известно из школьного курса математики, приводит всего навсего к умножению на константу. Это эквивалентно переходу к другой единице измерения, совершенно аналогично тому, как умножение на соответствующую константу происходит при переходе от метров к сантиметрам или от килограммов к граммам.

Таким образом, если измерение ведётся в двоичной системе, то H=log 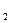N (бит), если в десятичной, то H=lgN (дит), если в экспотенциальной, то H=lnN (нат).

Пример. Чтобы узнать положение точки в системе из двух клеток, т.е. получить некоторую информацию, необходимо задать один вопрос (“левая или правая клетка?”). Узнав положение точки, мы увеличиваем суммарную информацию о системе на один бит (I=log 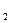2). Для системы из четырёх клеток необходимо задать два аналогичных вопроса, а информация равна двум битам (I=log 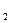4). Если система имеет n различных состояний, то максимальное количество информации равно I=log 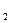n.

Справедливо утверждение Хартли: если во множестве 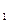X={x 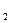,x ,…,x } выделить произвольный элемент x X, то, чтобы найти его, необходимо получить не менее log n (единиц) информации.

По Хартли, чтобы мера информации имела практическую ценность, она должна отражать количество информации пропорционально числу выборов.

Пример 1. Имеются 192 монеты, из которых одна фальшивая (легче настоящих). Определим, сколько взвешиваний нужно произвести, чтобы опознать её. Если положить на весы равное количество монет, то получим две возможности: а) левая чашка ниже; б) правая чашка ниже. Таким образом, каждое взвешивание даёт количество информации I= log 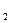2 =1 и, следовательно, для определения фальшивой монеты нужно сделать не менее k взвешиваний, где k удовлетворяет условию: log 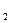2 ≥ log 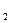192. Отсюда k ≥ 7. Следовательно, нам достаточно сделать 7 взвешиваний.

Пример 2. ДНК человека можно представить себе как некоторое слово четырёхбуквенного алфавита, где каждой буквой отмечено звено цепи ДНК (нуклеотид).Определим, сколько бит информации содержит ДНК, если в ней содержится примерно 1.5х10 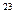нуклеотидов. На один нуклеотид приходится log 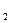4=2 бита информации. Следовательно, структура ДНК в организме человека позволяет хранить 3х10 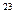бит информации, в том числе избыточной. В памяти человека информации хранится гораздо меньше.

Формула Хартли отвлечена от семантических и качественных, индивидуальных свойств рассматриваемой системы (качества информации, содержащейся в системе, в проявлениях системы с помощью рассматриваемых N состояний системы). Это основная положительная сторона этой формулы. Но имеется и существенный недостаток: формула Хартли не учитывает различимость и различность рассматриваемых N состояний системы. Уменьшение (увеличение) H может свидетельствовать об уменьшении (увеличении) разнообразия состояний N системы. Обратное, как это следует из формулы Хартли (основание логарифма берётся больше единицы!), также верно.

2. Мера Шеннона. Формула Шеннона даёт оценку информации независимо, отвлечённо от её смысла:

I= - ,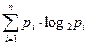

Где n – число состояний системы, p - вероятность (или относительная частота) перехода системы в i-е состояние, причём сумма всех равна 1. Если все состояния равновероятны (т.е. =1/n), то I= log 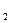n.

Покажем справедливость данной формулы.

Если все исходы (состояния) равновероятны, то каждый исход вносит в неопределённость одну и ту же лепту. Поскольку общая неопределённость равна log 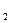n, то вклад в неё одного исхода составляет

Число 1/n – это вероятность каждого исхода, если они все равновероятны. Поэтому представляется естественным, что для неравновероятных исходов вклад информации одного исхода в общую неопределённость опыта составляет plog 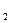p,где p – вероятность данного исхода. Если опыт имеет n исходов, а их вероятности равны 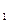p 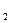, p ,…, p , то мера неопределённости для данного опыта в целом равна

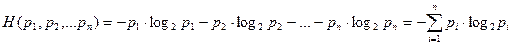
Так как информация понимается как снятая неопределённость (т.е. разность двух неопределённостей до и после проведения опыта), то можно записать:

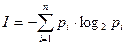
Эта формула показывает, какое максимальное количество информации можно получить о данной системе (в случае полного снятия неопределённости).

К. Шенноном доказана теорема о единственности меры количества информации. Для случая равномерного закона распределения плотности вероятности мера Шеннона совпадает с мерой Хартли. Справедливость и достаточная универсальность формул Хартли и Шеннона подтверждается и данными нейропсихологии.

Пример. Время t реакции испытуемого на выбор предмета из имеющихся N предметов линейно зависит от 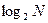: (мс). По аналогичному закону изменяется и время передачи информации в живом организме. В частности, один из опытов по определению психофизиологических реакций человека состоял в том, что перед испытуемым большое количество раз зажигалась одна из n лампочек, которую он должен был указать. Оказалось, что среднее время, необходимое для правильного ответа испытуемого, пропорционально не количеству n лампочек, а именно величине I, определяемой по формуле Шеннона, где 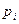- вероятность зажигания лампочки номер i.

Легко видеть, что в общем случае

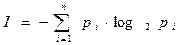
Если выбор i -го варианта предопределён заранее (т.е. выбора как такового нет, 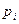=1), то I =0.

Сообщение о наступлении события с меньшей вероятностью несёт в себе больше информации, чем сообщение о наступлении события с большей вероятностью. Сообщение о наступлении достоверно наступающего события несёт в себе нулевую информацию.

Пример 1. Если положение точки в системе известно, скажем, она находится в k -ой клетке, то все ,кроме 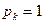, и тогда ,т.е. мы новой информации не получаем.

Пример 2. Выясним, сколько бит информации несёт каждое двузначное число со всеми значащими цифрами (отвлекаясь при этом от его конкретного числового значения). Так как таких чисел может быть всего 90 (от 10 до 99), то количество информации будет равно , или приблизительно I=6.5. Так как в таких числах значащая первая цифра имеет 9 значений (от 1 до 9), а вторая – 10 значений (от 0 до 9), то 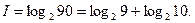Приблизительное значение 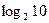равно 3,32. Итак, сообщение в одну десятичную единицу несёт в себе в 3,32 больше информации, чем в одну двоичную единицу (так как ), а вторая цифра, например в числе 22, несёт в себе больше информации, чем первая[6].

Если в формуле Шеннона обозначить 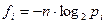, то получим, что I можно понимать как среднее арифметическое величин . Тогда можно интерпретировать как информационное содержание символа алфавита с индексом i и вероятностью 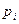появления этого символа в сообщении, передающем информацию.

Пусть сообщение состоит из n различных символов, 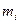- количество символов с номером i = 1,2,…,n в этом сообщении, а N – длина сообщения в символах. Тогда вероятность появления i – го символа в сообщении равна 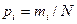. Соответственно, число всех различных сообщений длины n будет равно

а количество информации в одном таком сообщении – равно

Используя формулу Стирлинга (она достаточно точна, например, при N>100) - 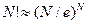, а точнее, её следствие - получаем (в битах):

.

Пример 1. Пусть рассматривается алфавит из двух символов русского языка – “к” и “а”. Относительная частота встречаемости этих букв в частотном словаре русского языка равна, соответственно, 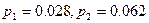. Возьмём произвольное слово p длины N из k букв “к” и m (k+m=N) букв “а” из этого алфавита. Число всех таких возможных слов, как это следует из комбинаторики, равно . Оценим количество информации в таком слове: . Воспользовавшись следствием приведённой выше формулы Стирлинга, получаем оценку количества информации (в битах) на один символ любого слова:

.

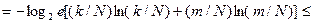
Пример 2. В сообщении содержатся четыре буквы “а”, две буквы “б”, одна буква “и” и шесть букв “р”. Определим количество информации в одном из всех возможных таких сообщений. Число N различных возможных сообщений длиной в 13 букв равно величине N = 13!/() = 180180. Количество информации I в одном сообщении равно величине бит.

Если k – коэффициент Больцмана, известный в физике как эрг/град, то выражение

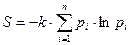
в термодинамике известно как энтропия или мера хаоса, беспорядка в системе. Сравнивая выражения I и S, видим, что I можно понимать как информационную энтропию (энтропию из-за нехватки информации о системе или в системе).

Нулевой энтропии соответствует максимальная информация. Основное соотношение между энтропией и информацией: или в дифференциальной форме .

Основными положительными сторонами формулы Шеннона являются её отвлечённость от семантических и качественных, индивидуальных свойств системы, а также то, что, в отличии от формулы Хартли, она учитывает различность, разновероятность состояний – формула имеет статистический характер (учитывает структуру сообщений), делающий эту формулу удобной для практических вычислений. Основные недостатки формулы Шеннона: она не различает состояния (например, с одинаковой вероятностью достижения), не может оценивать состояния сложных и открытых систем и применима лишь для замкнутых систем, отвлекаясь от смысла информации.

Увеличение (уменьшение) меры Шеннона свидетельствует об уменьшении (увеличении) энтропии (организованности) системы. При этом энтропия может являться мерой дезорганизации системы от полного хаоса (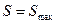) и полной информационной неопределённости (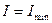) до полного порядка () и полной информационной определённости (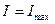) в системе.

Пример. Чем ближе движущийся объект к нам, тем полнее информация, обрабатываемая нашими органами чувств, тем чётче структурирован (упорядочен) и объект. Чем больше информации мы имеем о компьютерной технике, тем меньше психологический барьер перед ней (согласно основному соотношению между энтропией и информацией).

Кроме указанных выше подходов к определению меры информации есть и много других (меры Винера, Колмогорова, Шрейдера и др.), но основными методами (в образовательной информатике) являются рассмотренные.

[1] Наличие смысла – свойство “полезной” информации. Многие исследователи настаивают на том, что информация может отражать и бессмыслицу. Например, Е. А. Медведева в своей статье [2, с. 21] освещает этот вопрос так: “…информация отражает не только смысл, но и бессмыслицу, не только упорядоченность, но и беспорядок (хаос). Полагаем, что это очень важно в понимании природы информации. До настоящего времени информацию связывали только со смыслом и порядком, противопоставляя её хаосу. Такое одностороннее и методологически ошибочное видение информации может и должно быть преодолено”.

[2] Бит (от англ. BI nary digi T) – двоичная цифра.

[3] Байт – единица количества информации в системе СИ.

[4] Данное замечание делается с опорой на то, что наличие смысла рассматривается как характеристическая черта информации, что в новых теориях, распространяющих понятие информации и на отражение хаоса, не выполняется.

[5] В математике доказывается, что монотонная функция f(x), обладающая свойством f(x+y)=f(x)+f(y) и обращающаяся в 0 при x=1, обязана быть логарифмической функцией.

[6] Имеется в виду случай, когда цифра в этом разряде неизвестна, иначе никакого выбора нет и информация равна нулю.