Представим интеграл Фурье
в виде:
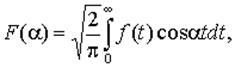(1)
(2)
Функция F(
), определенная формулой (1), называется косинусом-преобразованием Фурье для f(x).
Формула (2) задает обратное косинус – преобразование Фурье, позволяющее по F (a) находить f(x).
Аналогично, если f(x) – нечетная функция, то A(a) = 0, тогда формулы (3) и (4) задают соответственно прямое и обратное синус-преобразование Фурье
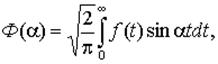(3)
(4)
Если интеграл Фурье в комплексной форме представить в виде
(5)
то функция S(a) также называется спектральной и S (a) = 2p C (a).
Преобразованием Фурье называется функция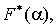 
определенная формулой (6)
(6)
а функция f(x), определенная формулой (7) называется обратным преобразованием Фурье
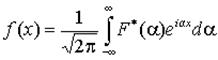(7)
Преобразование Фурье отличается от спектральной функции только множителем
(
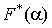также называется спектральной функцией).
Если функция f(x) – оригинал с показателем роста 
, то функция g(x), определенная формулой 
, где 
называется затухающим оригиналом. Тогда для функции g(x) существует и преобразование Фурье и преобразование Лапласа и они связаны между собой формулой
(8)
