Цель: изучение методов решения систем нелинейных алгебраических и трансцендентных уравнений, практическое решение системы уравнений на ЭВМ, сравнительный анализ рассмотренных методов.
, где 
; 
.
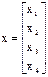Метод Ньютона
Матрица Якоби:
.
Пусть задано начальное приближение x[0]. Функцию f(x) линеаризуют в точке x[0], разлагая ее в ряд Тейлора с точностью до членов первого порядка.
Тогда f(x)=0 Þ f(x)=f(x[0])+J([x-x[0])=0.
Получаем линейную систему уравнений. Если J(x[0]) не вырождена, то эта система имеет единственное решение x[1]. Линейную систему удобно решать относительно поправки Dx[0]=x-x[0], а затем вычислять очередное приближение x[1]=x[0]+Dx[0]. В общем случае: x[m+1]=x[m]+Dx[m], где Dx[m] решения линейной системы f(x[m])+J(x[m])Dx[0]=0 или в координатной форме:
Метод Ньютона эффективен в достаточно малой окрестности корня (здесь он обладает квадратичной сходимостью).
Критерий итерации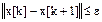 
Метод Зейделя
Систему заменяют эквивалентной системой:
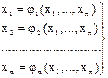или 
Такая система может быть получена следующим образом: 
, где 
. Задают начальное приближение x[0] и осуществляют процедуру Зейделя:
, i=1,...,n,
т.е. уже вычисленные приближения неизвестных x1[k+1],...,xi-1[k+1] используются для вычисления x1[k+1].
Условия прекращения
, i=1,...,n.
Сложно получить систему x-j(x) эквивалентную исходной и обеспечивающую сходимость.
