Параметрическое программирование
#0 - всегда нуль. Этой переменной нельзя присвоить никакого значения.
#1 - #33 – Локальные переменные. При отключении питания обнуляются.
#100 - #199 – Общие переменные. При отключении питания обнуляются.
#500 - #999 – Общие переменные. При отключении питания данные сохраняются.
Диапазон значений переменных:
от -1047 до -10-29
от +10-29 до +1047
Примеры:
#1=123
X#1
Z[#1/2]
Ограничения использования:
Нельзя использовать переменные в качестве номера программы (O#10),
в качестве номера кадра (N#20) и после наклонной черты в начале кадра (/#30).
Действия с переменными:
4 арифметических действия + - * /
SIN[…](синус), COS[…],TAN[…], ASIN[…](арксинус), ACOS[…], ATAN[…]
SQRT[…](квадратный корень), ABS[…](модуль числа), ROUND[…](округление),
FIX[…](округление в меньшую сторону), FUP[…](округление в большую сторону),
LN[…], EXP[…],
OR(логическое ИЛИ), XOR(исключающее ИЛИ), AND(логическое И).
Операторы сравнения:
GT больше
LT меньше
EQ равно
NE не равно
GE больше или равно
LE меньше или равно
Переходы и повторы:
GOTO100 – Переход на кадр N100, безусловный
IF [#1GT10] GOTO100 – Переход на кадр N100, если #1>10
IF [#1GT10] THEN #2=20 – Присвоение #2=20, если #1>10
WHILE [#1GT10] DO1
#1=#1+1
G0 X#1
END1
 Пример параметрической программы:
Пример параметрической программы:
Токарная обработка
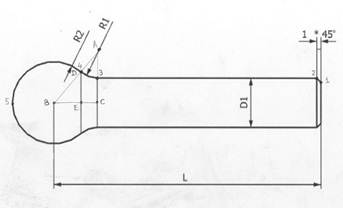
Напишем чистовую обработку такого валика, размеры которого сведены в таблицу:
| Деталь | D1 | L | R1 | R2 |
| 000.00.00 | ||||
| 000.00.00-01 | ||||
| 000.00.00-02 | ||||
 000.00.00-03 000.00.00-03
|
В начале программы введем переменные:
O0001(PRIMER 1)
N10 #501=12(D1)
N40 #504=65(L)
N50 #505=5(R1)
 N60 #506=10(R2)
N60 #506=10(R2)
Чтобы выполнить чистовую обработку, нам необходимо знать координаты всех опорных точек. Обозначим эти точки цифрами и буквами.
1 (#1;#2) (#1 – координата точки 1 по оси X, #2 - по оси Z)
2 (#3;#4)
3 (#5;#6)
4 (#7;#8)
5 (#9;#10)
A (#11;#12)
B (#13;#14)
Теперь присвоим этим переменным известные значения:
Точка 1 – начало траектории, ее координата по X будет равна значению диаметра D1 уменьшенного на двойную величину фаски 1*45°, т.е. D1-2. Значение D1 хранится в переменной #501, тогда получим наше первое вычисление
N70 #1=#501-2
Координата точки 1 по Z равна нулю,
N80 #2=0
Далее, для точки 2:
N90 #3=#501
N100 #4=-1
Для точки 3 мы пока знаем только координату по X:
N110 #5=#501
Для точки 4 неизвестны пока обе координаты, пропустим ее, и укажем оставшиеся известные значения:
N120 #9=0
N130 #10=-#504-#506
N140 #11=#501+#505*2
Здесь, по правилам математики, система сначала выполнит умножение (#505*2), а затем сложение
N150 #13=0
N160 #14=-#504
Выделим известные координаты наших точек:
1 ( #1;#2)
2 (#3;#4)
3 (#5;#6)
4 (#7;#8)
5 (#9;#10)
A (#11;#12)
B (#13;#14)
Теперь определим оставшиеся 4 неизвестные пока координаты:
Чтобы найти координату точки 3 по Z, нужно найти величину отрезка BC.
Условие касательного сопряжения дуг определяет, что прямая AB проходит через точку 4.
Рассмотрим треугольник ABC:
Он прямоугольный, по теореме Пифагора, AB2=BC2+AC2
Тогда, BC2= AB2-AC2
BC=Корень_квадратный(AB2-AC2)
AB=R1+R2
AC=D1/2+R1
Теперь запишем это в нашу программу, используя для вычислений промежуточные переменные:
N170 #15=#505+#506 (AB)
N180 #16=#15*#15 (AB2)
N190 #17=#501/2+#505 (AC)
N200 #18=#17*#17 (AC2)
N210 #19=SQRT[#16-#18] (BC)
Точка 3 лежит правее точки B на известную теперь величину BC:
N220 #6=#14+#19
Координата точки A по Z совпадает с координатой точки 3 по Z.
N230 #12=#6
Осталось определить неизвестную точку 4.
Треугольники ABC и DBE подобны, следовательно
BE/BC = BD/BA
Тогда,
BE = BD/BA*BC
Напомню, BD=R2, BA=R1+R2, BC – уже известно и равно #19
Тогда, запишем в программу
N240 #20=#506/[#505+#506]*#19 (BE)
Точка 4 лежит правее точки B на величину BE:
N250 #8=#14+#20
Аналогично, из подобия тех же треугольников:
N260 #21=#506/[#505+#506]*#17 (DE)
N270 #7=#21*2
Итак, все точки определены.
Составим теперь из них траекторию.
N280 G1 X#1 Z#2
N290 X#3 Z#4
N300 Z#6
N310 G2 X#7 Z#8 R#505
N320 G3 X#9 Z#10 R#506
Мы получили универсальную программу, в которой, меняя исходные данные, мы можем получить сколько угодно разных деталей.






