А.М. Ляпунов не только строго поставил задачу об устойчивости, но и предложил два метода решения этой задачи (теперь их называют первым и вторым методами Ляпунова).
Первый метод связан с построением решений уравнений возмущенного движения в виде рядов (наибольшее применение этот метод находит при рассмотрении так называемых критических случаев, когда первое приближение не решает задачи).
Второй метод (он же прямой метод или метод функций Ляпунова) состоит в отыскании некоторых функций, свойства которых позволяют по их поведению вдоль траекторий уравнений возмущенного движения делать заключение об устойчивости невозмущенного движения.
Используя свой второй метод, Ляпунов выделил те случаи, в которых вопрос об устойчивости полностью решается рассмотрением первого приближения уравнений возмущенного движения (результаты сформулированы в виде теории об устойчивости по первому приближению).
В случае, когда уравнения возмущенного движения явно не зависят от времени (т.е. для установившихся движений) имеют место такие утверждения:
1) Если действительные части всех корней характеристического уравнения системы первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво при любых нелинейных членах (говорят – асимптотически устойчиво по первому приближению)
2) Если действительная часть хотя бы одного корня положительна, то невозмущенное движение неустойчиво, каковы бы ни были остальные корни характеристического уравнения и нелинейные члены уравнений возмущенного движения (говорят – невозмущенное движение неустойчиво по первому приближению)
3) Если же характеристическое уравнение, не имея корней с положительной действительной частью, имеет корни на мнимой оси (т.е. с нулевыми действительными частями ), то первое приближение не решает задачи, и выбором нелинейных членов невозмущенное движение можно сделать как асимптотически устойчивым, так и неустойчивым (возможна и ситуация неасимптотической устойчивости). Такие случаи называются критическими (Ляпунов называл их особыми).
Иногда в такой ситуации, не исследуя нелинейных членов, говорят, что невозмущенное движение устойчиво в первом приближении. Это надо понимать так: нет грубой (асимптотической по первому приближению) устойчивости, но нет и грубой (по первому приближению) неустойчивости, причём до конца задача не решена, просто по первому приближению ответа получить не удалось.
С точки зрения математики критические случаи являются исключительными (их, казалось бы, намного меньше, чем некритических, в которых первое приближение решает задачу). Но с точки зрения приложений эта категория ситуаций весьма важна, поскольку для многих практически важных задач устойчивость возможна лишь в критических случаях либо более простыми случаями устойчивости для таких систем являются именно критические. Примерами таких задач являются задачи об устойчивости равновесий консервативных систем (т.е. таких, для которых имеет место интеграл энергии), задачи об устойчивости стационарных движений (таких движений, на которых часть координат, а также скорости остальных координат сохраняют постоянные значения).
Необходимость рассмотрения задач об устойчивости в критических случаях следует уже из того, что именно стационарные движения являются рабочими режимами подавляющего большинства современных технических устройств (именно так движется большинство искусственных спутников Земли, гироскопические навигационные приборы, турбины, электроприводы в установивших режимах и т.п.).
Решение задачи об устойчивости в критических случаях по сравнению с рассмотрением некритических случаев намного усложняется, так как теперь необходим анализ нелинейных членов уравнений возмущенного движения, причем, как правило, заранее неизвестно, до какого порядка нужно проводить этот анализ.
О критических случаях Ляпунов написал: «случаи такого рода весьма разнообразны, и в каждом из них задача получает свой особый характер, так что не может быть и речи о каких-либо общих способах ее решения, которые относились бы ко всем таким случаям». Это было написано более 100 лет назад, в предисловии к «Общей задаче об устойчивости движения» для общей ситуации критического случая. С тех пор (для специальной ситуации критических случаев, когда действительные части некоторых корней характеристического уравнения отрицательны), в основном, усилиями Каменкова Г.В. и Малкина И.Г. разработан восходящий к самому Ляпунову так называемый принцип сведения, который позволяет судить об устойчивости невозмущенного движения для полной системы, исходя из решения вопроса об устойчивости нулевого решения так называемой укороченной системы. В эту систему входят только те переменные, которым отвечают корни характеристического уравнения с нулевыми действительными частями (эти переменные называются критическими).
Мы проиллюстрируем применение этого принципа к решению задачи в критическом случае одного нулевого корня. Напомним, что для этого случая задача была полностью решена Ляпуновым в «Общей задаче об устойчивости движения». Итак, допустим, что уравнения возмущенного движения
(1)
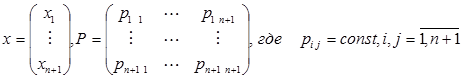
таковы, что характеристическое уравнение
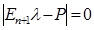(2)
кроме одного нулевого корня, имеет n корней с отрицательными действительными частями. Здесь верхний индекс в скобках означает порядок младших членов в разложении соответствующего выражения, а штрих – транспонирование.
В критических случаях, как выше уже было сказано, ответ получается с учетом нелинейных членов, теперь можно сказать точнее – решение вопроса зависит от того, каким образом критические переменные входят в правые части уравнений возмущенного движения. Для этого, прежде всего, нужно выделить эти критические переменные (у нас сейчас такая переменная одна). Процедура такого выделения называется приведением уравнений возмущенного движения к специальному виду. С этой целью, следуя Ляпунову, введем новую переменную
(3)
Здесь постоянные коэффициенты 
будем выбирать таким образом, чтобы полная производная 
(4)
не содержала членов первого порядка. Отсюда имеем
(5)
Левая часть выражения (5) является линейной формой, которая для любых значений своих переменных должна обращаться в нуль, что, очевидно, возможно только при нулевых значениях коэффициентов. Вследствие этого получаем однородную линейную систему уравнений для определения
(6)
Определитель матрицы коэффициентов в системе (6) равен нулю, поскольку уравнение (2) имеет нулевой корень. Поэтому при рассматриваемом расположении корней из (6) всегда можно однозначно определить нетривиальный набор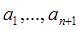 
. Допустим, что в этом наборе отлична от нуля, в частности, 
. Тогда из (3) можем найти
(7)
Сделаем теперь в системе (1), с учетом (3) и (7), замену
(8)
Будем иметь 
(9) 
Характеристическое уравнение системы (9)
(10)
распадается на уравнение 
=0 и уравнение
(11)
Поскольку корни характеристического уравнения не изменяются при неособенном линейном преобразовании (а преобразование (8) именно такое), то корни уравнения (10) и уравнения (2) одни и те же, поэтому действительные части всех корней характеристического уравнения (11) отрицательны.
Итак, в случае, когда характеристическое уравнение имеет один нулевой корень и действительные части остальных его корней отрицательны, уравнение возмущенного движения всегда можно привести к виду (9). Это – специальный вид уравнений возмущенного движения в критическом случае одного нулевого корня и у здесь критическая переменная.
Теперь мы знаем, какой переменной отвечает критический (у нас это нулевой) корень характеристического уравнения. Следующий этап в исследовании – анализ зависимости правых частей уравнений возмущенного движения (в специальном виде) от критических переменных (у нас сейчас это переменная у): требуется определить минимальный порядок свободно входящих критическихпеременных в так называемой присоединенной (соответствующей некритическим переменным) и в укороченной (система для критических переменных, в которой все некритические переменные приравнены нулю) системах. Для этого следует приравнять нулю в правых частях системы (9) все некритические переменные – в нашем случае это – все у i. В результате получаем
(12)
(13)
В теории устойчивости традиционно используются обозначения
(14)
В нашем случае каждая из функций (14) – функция одной из переменной у, которая может быть разложена в ряд по степеням у, так что
(15)
Очевидно, что если хотя бы один из коэффициентов qi отличен от нуля, порядок свободно входящей критической переменной у в правых частях присоединенной системы (а это – выражение (12)) – первый, в то время как в правой части укороченной системы (у нас сейчас это – выражение (13)) этот порядок не ниже второго, поскольку разложение правой части последнего уравнения системы (9) начинается с членов не меньше второго порядка.
Ляпунов показал, что ответ на вопрос об устойчивости нулевого решения полной системы (9) будет такимже, как для укороченной системы, если минимальная степень свободно входящей критической переменной в присоединенной системе не ниже, чем в укороченной. Такая ситуация называется частнымслучаем критического случая одного нулевого корня.
Очевидно, для этого должны быть выполнены условия
(16)
В этом случае путем явного построения функций Ляпунова с использованием теорем Ляпунова об асимптотической устойчивости и неустойчивости (в более сложных критических случаях Г.В. Каменков использовал и теорему Н.Г. Четаева о неустойчивости) доказано, что при условиях (16) вопрос об устойчивости невозмущенного движения для полной системы полностью решается рассмотрением вопроса для укороченной системы – в нашей задаче сейчас эта система – единственное уравнение
(17)
Рассмотрим эту последнюю задачу.
Допустим сначала, что m – чётное число. Докажем, используя теорему Ляпунова о неустойчивости, что в этом случае нулевое решение уравнения неустойчиво. Выберем в качестве функции Ляпунова V1=y. Тогда её производная по времени получает вид:
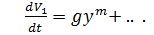
и, таким образом является знакоопределенной функцией (так как m – чётное число), знак которой совпадает со знаком g. Таким образом, функция V 1 удовлетворяет условиям первой теоремы Ляпунова о неустойчивости.
Пусть теперь m – нечётное число. Возьмём функцию Ляпунова в виде 
. Её полная производная в силу уравнения
будет в некоторой окрестности нуля знакоопределенной функцией (так как теперь m+1 – чётное число), знак которой совпадает со знаком g. Поскольку сама функция V2 положительно определённая, то в случае g < 0 она удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости ( V2 определённо-положительна, её производная – определённо-отрицательна). Если же g > 0, то V2 удовлетворяет условиям первой теоремы Ляпунова о неустойчивости (см. выше).
Резюмируя проведённые рассуждения, имеем:
Если при условиях (16) (т.е. в частном случае) g < 0 и m – нечётное число, то невозмущённое движение для полной системы устойчиво асимптотически, во всех других ситуациях (m – чётное, g – любое, или m – нечётное и g > 0) невозмущенное движение неустойчиво.
Пусть теперь условия (16) не выполнены. Тогда мы имеем так называемый общий случай критического случая нулевого корня. Для этого, очевидно, достаточно, чтобы хотя бы один коэффициент qk был отличен от нуля, т.е. хотя бы в одном из уравнений присоединённой системы присутствовал линейный по критической переменной член. Ляпунов предложил способ сведения общего случая к частному. Для этого предлагается в системе (9) выполнить, вообще говоря, нелинейную замену переменных по некритическим переменным
(18)
где hi – новые некритические переменные, а ui(y) – неизвестные пока функции, которые будем выбирать так, чтобы свести ситуацию к частному случаю, т.е. чтобы
(19)
Система уравнений (19) получена после замены (18) из первых n уравнений системы (9), в которых затем новые некритические переменные приравнены нулю. Функции ui(y) будем искать в виде формально удовлетворяющих системе (19) рядов
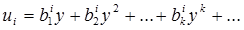(20)
Ряды (20), как отмечал Ляпунов, как правило, будут расходящимися. Но их сходимость и не нужна, если вопрос об устойчивости решается по членам некоторого конечного порядка N (число N может отличаться, вообще говоря, от первоначального m, так как замена (18) изменяет правые части уравнений (9)). В этом случае, очевидно, достаточно в рядах (20) взять сумму первых членов до порядка N. Если же этот конечный порядок N не удаётся установить (например, если 
), то в замене (18) нужно брать сумму всех членов рядов, до бесконечно высоких степеней, т.е. нужна их сходимость. Но в этой ситуации, как показал Ляпунов, а для более сложных критических случаев – Г.В. Каменков (так называемая теорема о существовании решения уравнений в частных производных) при некоторых условиях, одним из которых в теореме Каменкова является условие
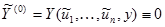(21)
как раз и имеет место сходимость. Здесь и далее обозначение 
показывает, что в аргументах соответствующих функций подставлены полные сходящиеся ряды (20), которые в этой ситуации обозначим 
. Поэтому в новых переменных правые части преобразованной заменой (18) системы (9) при hi = 0 тождественно равны нулю, вследствие чего система
(22)
допускает решение вида
(23)
Такой случай называется особенным случаем критического случая одного нулевого корня. Очевидно, для таких задач, которые сводятся к особенным случаям, асимптотическая устойчивость по отношению ко всем переменным невозможна: невозмущенное движение соответствует точке
(24)
а, согласно (23), можно взять начальное возмущение
(25)
причём точка (25) является решением уравнения (22), которое, очевидно, не будет асимптотически стремиться к невозмущенному движению (24). Привлекая результаты теории устойчивости по отношению к части переменных, можно установить асимптотическую устойчивость по отношению к 
. При возвращении к переменным y, yi в общем случае асимптотически устойчивых переменных может не оказаться, если замена (18) проводилась по всему вектору yi, так как
, а 
.
Ещё раз повторим алгоритм исследования устойчивости в критическом случае одного нулевого корня:
Если уравнение (2) имеет один нулевой корень и n корней с отрицательными действительными частями, следует:
1. Привести уравнения возмущенного движения к специальному виду с помощью линейной замены (8);
2. Установить минимальный порядок свободно входящей переменной y в правых частях уравнений возмущенного движения (9), для чего достаточно приравнять нулю все yi;
3. Если выполнены условия (16) – получим частный случай, для которого имеет место асимптотическая устойчивость при g < 0 и нечётном m, во всех остальных ситуациях имеет место неустойчивость.
4. Если условия (16) не выполнены, получаем общий случай, для сведения которого к частному или особенному необходима замена (18), где ui ищутся в виде рядов (20), коэффициенты которых можно последовательно определить, начиная с коэффициентов при членах младших порядков. Если после замены (18) исследование сведётся к частному случаю, вопрос решается аналогично тому, как он решался в предыдущем пункте и, следовательно, будем иметь асимптотическую устойчивость или неустойчивость;
5. Если же задача свелась к особенному случаю, то получим (см. (22)) только неасимптотическую устойчивость.
Отметим одно отличие алгоритма применения принципа сведения в более сложных критических случаях, когда число критических переменных больше единицы, причем среди корней могут быть и чисто мнимые. Здесь следует сравнивать минимальный порядок 
свободно входящих критических переменных в присоединенной системе не с порядком свободно входящих критических переменных в присоединенной системе, а тем порядком, по которому получено заключение об устойчивости для укороченной системы.
Пример1. Пусть уравнения возмущенного движения и характеристическое уравнение имеют вид (все величины сейчас скалярные)
(26) 
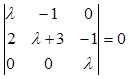
Причем у этого уравнения один нулевой корень и два корня с отрицательными действительными частями. Третье уравнение не содержит линейных членов. Здесь, в отличие от общей ситуации, сразу имеем специальный вид теории критических случаев: нулевой корень соответствует переменной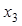 
он выносится из третьей строки, соответствующей переменной 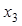, а остальным двум переменным соответствуют корни с отрицательными действительными частями, т.е. 
являются некритическими переменными. Приравнивая, в соответствии с алгоритмом принципа сведения, некритические переменные нулю, имеем в качестве членов правых частей, содержащих только свободно входящую критическую переменную, выражения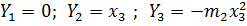 
Таким образом, имеем общий случай критического случая одного нулевого корня (в присоединенной системе младший порядок свободно входящей критической переменной первый, в укороченной второй) и для сведения его к частному необходима замена (18), в которой искомые функции здесь получают форму
(27)
Подставляя (18) с функциями (27) в присоединенную систему (первые два уравнения системы (26)) и приравнивая нулю новые некритические переменные 
, имеем
(28)
откуда 
, и в присоединенной системе критическая переменная свободно входит теперь только со второй степени включительно. Подставив замену (18) с функциями (27) при таком b, запишем укороченную систему - у нас сейчас это одно уравнение
(29)
Как видим, если
(30)
то порядок свободно входящей переменной в укороченной системе после замены (18) станет равным, по крайней мере, трем, и тогда в присоединенной системе придется определять следующий коэффициент в разложении 
, чтобы убрать в этой системе свободно входящую критическую переменную во второй степени. Тогда младший порядок свободно входящей критической переменной станет равным трем (т.е. нечетным) и вопрос об устойчивости будет решаться, в зависимости от соотношения величин 
. Если же условие (30) не выполнено, порядок свободно входящей переменной в укороченной системе равен двум, т.е. четное число, а, согласно пункту 3), в такой ситуации всегда имеет место неустойчивость.
Пример 2. Изменяя нелинейные члены в третьем уравнении предыдущей системы, покажем, как общий случай критического случая может быть сведен к особенному случаю. Итак, пусть уравнения возмущенного движения таковы
(31)
Поскольку линейные члены не менялись, имеем общий случай критического случая одного нулевого корня, соответствующего переменной 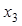. Степень свободно входящей критической переменной в присоединенной системе по-прежнему первая, в укороченной же системе свободно входящей критической переменной нет – т.е. эта степень 
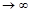. Выполнив замену вида (18) при искомых функциях (27), в результате получим ситуацию особенного случая, т.к. в третьем уравнении правая часть обращается в нуль при 
, а во втором уравнении правая часть обратится в нуль за счет выбора функции 
. Таким образом, получим асимптотическую устойчивость по отношению к 
и неасимптотическую по отношению к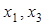 
. При этом устойчивость по отношению к 
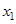становится неасимптотической вследствие замены (18): если дать системе начальные возмущения 
, то возмущенное движение будет асимптотически стремиться к точке 
.
Задания для самостоятельной работы:
Исследовать устойчивость решения (0,0,0) для системы третьего порядка
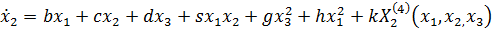
При этом численные значения постоянных коэффициентов определяются для каждого варианта выражениями:
Здесь N – порядковый номер студента в списке группы.
