Рассмотрим отдельно четные и нечетные отсчеты спектра (отсюда и название алгоритма: прореживание по частоте)

Для получения четных отсчетов спектра положим

k = 2 i, где i = 0, 1, 2,.. N /2 -1.

 

В результате получим

 

.

Для получения нечетных отсчетов спектра положим

k = 2i + 1, где i = 0, 1, 2,.. N/2-1.

Тогда

Два последних соотношения представляют собой

N / 2 - точечные ДПФ последовательностей и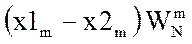

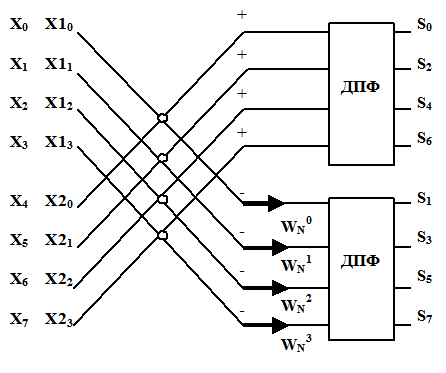
Образовавшиеся после первого разбиения блоки ДПФ подвергаются дальнейшему разбиению подобно тому, как это делалось в предыдущем алгоритме с прореживанием во времени.

Оба алгоритма равноценны.

 

4.5. Вейвлет-преобразование

 

4.5.1. Вейвлет-преобразование аналогового сигнала

 

Недостатком прямого преобразования Фурье при анализе спектра сигнала является невозможность оценить характер изменения спектра во времени, т.к. при определении спектральной плотности интегрирование по времени осуществляется в пределах от

.

Сигнал в виде суммы двух синусоидальных колебаний, действующих одновременно, и его спектр

 

Сигнал, образованный двумя синусоидальными колебаниями, действующими поочередно, и его спектр

 

 

Из сравнения последних рисунков следует, что сигналы, существенно отличающиеся друг от друга, имеют практически одинаковый спектр, полученный методом ДПФ.

Этот недостаток частично устраняется при использовании оконного преобразования Фурье, которое определяется следующим соотношением

,

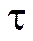где - оконная функция, - временной сдвиг оконной функции относительно начала координат (t = 0).

Анализируемый сигнал и оконная функция

Типичной оконной функцией является функция Гаусса

.

С помощью оконной функции оценивается спектр сигнала на ограниченном временном интервале, а перемещение окна позволяет выявить временные характеристики спектра.

Однако при использовании оконного преобразования Фурье возникает проблема выбора ширины окна. При малой ширине окна получается хорошее временное разрешение, но плохое частотное, при широком окне – наоборот.

Возможности изменения ширины окна это преобразование не предоставляет. Кроме того базисными функциями оконного преобразования, как и обычного преобразования Фурье остаются гармонические функции, которые хорошо описывают плавно изменяющийся сигнал, но плохо приспособлены для выделения скачков сигнала.

 

Указанных недостатков лишено вейвлет-преобразование. Непрерывное вейвлет-преобразование аналогового сигнала x(t) определяется следующим соотношением

,

где 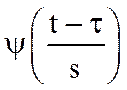- вейвлет.

В обозначении функции 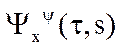нижний индекс x соответствует анализируемой функции x(t), а верхний индекс – вейвлету .

Слово «вейвлет» означает маленькая волна. Эта волна имеет конечную длительность и может рассматриваться как оконная функция.

Параметры этой функции:

- параметр сдвига относительно начала координат,

s – параметр масштаба, определяющий ширину вейвлета. Большие значения масштаба позволяют получить глобальное представление о сигнале, а малые значения позволяют различать детали.

При и s = 1 вейвлет называется материнским вейвлетом

Материнский вейвлет должен удовлетворять условию

Существует большое количество различных вейвлетов.

Вейвлет “Мексиканская шляпа” при разных значениях

параметра s

 

Вейвлет “Мексиканская шляпа” при разных значениях

параметра

 

Процедура анализа сигнала стартует с масштаба s = 1. Вейвлет сначала помещается в начало координат, умножается на сигнал и результат умножения интегрируется на всем временном интервале. Затем он сдвигается вправо на величину τ и описанная процедура повторяется. Затем масштаб увеличивается и снова осуществляется перемещение вейвлета вдоль оси времени.

Значение s = 1 соответствует сжатому вельвету и позволяет выявить высокочастотные составляющие сигнала. Большие значения масштаба выделяют низкочастотные составляющие сигнала.

 

4.5.2. Дискретизация непрерывного вейвлет-преобразо-

вания

 

Для осуществления непрерывного вейвлет-преобразования на ЭВМ необходимо задавать дискретные значения параметров вейвлета s и .

Частотно-временная плоскость

 

По оси ординат вместо s для удобства отложена величина логарифма s по основанию 2.

Интуитивно понятно, что чем шире вейвлет, тем больше можно выбрать шаг изменения .

На рисунке s = 1,2,4,8.., и при каждом удвоении масштаба интервал дискретизации также увеличивается в 2 раза.

Плоскость, представленную на рисунке, принято называть частотно-временной плоскостью, т.к. масштаб s связан с частотой анализируемого сигнала: большему масштабу соответствуют более низкие частоты.

Сигнал, образованный суммой двух синусоидальных

колебаний

 

 

Вейвлет-преобразование сигнала

 

Вейвлет-преобразование представлено в трехмерной системе координат и картой линий уровня в системе координат «сдвиг-частота» с учетом того, что уменьшению масштаба соответствует увеличение частоты.

Линией уровня называется линия вдоль которой величина функции, заданной на плоскости двух переменных, остается постоянной.

Увеличенный фрагмент карты линий уровня

 

 

Одновременному существованию двух синусоидальных колебаний соответствует однородная во времени структура вейвлет-преобразования с выраженными периодами, соответствующими низкочастотной и высокочастотной синусоидам.

 

Сигнал, образованный двумя синусоидальными колебаниями, действующими поочередно

 

 

Вейвлет-преобразование сигнала

 

Переходу от низкочастотной к высокочастотной синусоиде соответствует резкое изменение во времени структуры вейвлет-преобразования. Таким образом, информативность вейвлет-преобразования значительно выше информативно- сти преобразования Фурье.

 

4.5.3. Дискретное вейвлет-преобразование

 

При дискретном вейвлет – преобразовании частотно-временное представление сигнала получается с использованием методов цифровой фильтрации и субполосного кодирования.

Алгоритм реализации дискретного вейвлет-преобразования

 

Входной сигнал , спектр которого находится в интервале Котельникова от 0 до поступает на фильтры верхних и нижних частот, на выходах которых ширина спектра в два раза уже по сравнению с шириной спектра на входе.

Это позволяет выполнить прореживание отсчетов выходных сигналов фильтра с коэффициентом 2, т.е. уменьшить частоту дискретизации в два раза. На выходе прореживателя ФВЧ верхнего уровня получают коэффициенты дискретного вейвлет-преобразования (ДВП) первого уровня.

С выхода прореживателя ФНЧ сигнал поступает на входы ФНЧ и ФВЧ второго уровня. На их выходах действует сигнал с шириной спектра 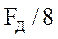, что позволяет уменьшить частоту дискретизации еще в два раза. На выходе прореживателя ФВЧ второго уровня получаются коэффициенты ДВП второго уровня. Этот процесс повторяется до тех пор, пока не будут пройдены все наперед заданные уровни анализа сигнала.

При непрерывном вейвлет-преобразовании изменялся масштаб окна анализа. При дискретном вейвлет-преобразовании изменяется частота среза фильтра.

Входной сигнал x_n и сигналы на выходах ФНЧ шести уровней x1_n..x6_n