ѕрактична ≥ лабораторна робота 3 з дисципл≥ни Дћоделюванн€ системФ.
ƒосл≥дженн€ лог≥стичного р≥вн€нн€.
ѕовед≥нку попул€ц≥њ, чисельн≥сть €коњ стаб≥л≥зуЇтьс€ на де€кому заданому р≥вн≥, часто описують за допомогою лог≥стичного р≥вн€нн€
dx / dt = rx (1- X / k),(1)
де параметр k задаЇ максимальну густину попул€ц≥њ.
–≥вн€нн€ (1) Ї нел≥н≥йним звичайним диференц≥альним р≥вн€нн€м першого пор€дку. ÷е р≥вн€нн€ завд€ки простот≥ маЇ анал≥тичний розвТ€зок
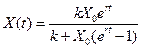 , (2)
, (2)
де X 0 Ц початкове значенн€ X (t).
Ќеважко пом≥тити, що функц≥€ (2) за малих t поводить себе €к X 0 ert, тобто Ї розвТ€зком л≥н≥йного диференц≥ального р≥вн€нн€ dx / dt = rx, ≥ лише ≥з зростанн€м t ви€вл€Їтьс€ нел≥н≥йн≥сть р≥вн€нн€ (1).
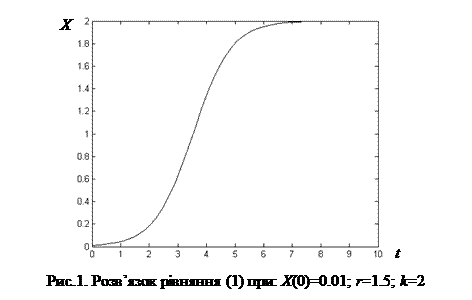
ћожливий розвТ€зок лог≥стичного р≥вн€нн€ (1) показано на рис.1.
Ўироке використанн€ лог≥стичного р≥вн€нн€ дл€ моделюванн€ розвитку попул€ц≥й по€снюЇтьс€ його простотою ≥ такими властивост€ми:
Ц за малих X р≥вн€нн€ (1) зводитьс€ до л≥н≥йного р≥вн€нн€ dx / dt = rx, тобто р≥ст ≥де експоненц≥ально дл€ малих X;
Ц дл€ б≥льших X величина X з часом пр€муЇ до пост≥йного значенн€ k.
“екст програми на мов≥ MATLAB-6 наступний.
%********* ELABORATION of LOGHISTICТs EQUATION *************
%********* ќсновна програма ********************************
сlear;
tlimit=[0, 10]; X0=[0.01];
[t,X]=ode45(@logeq,tlimit,X0);
plot(t,X)
%******** ¬м≥ст файлу logeq.m ********************************
function dXdt=logeq(t,X)
dXdt=[ 1.5*X*(1-X/2) ];
¬ основн≥й програм≥ п≥сл€ очищенн€ робочоњ област≥ памТ€т≥ оператором сlear; задаЇтьс€ часовий ≥нтервал розвТ€зуванн€ лог≥стичного р≥вн€нн€ tlimit ≥ початкова умова X0.
ƒал≥ знаходимо два вектори розвТ€зку лог≥стичного р≥вн€нн€ [t,X] за допомогою функц≥њ ode45, що розвТ€зуЇ за методом –унге- утта четвертого пор€дку. јргументами функц≥њ ode45 Ї ≥мТ€ файла з описом диференц≥ального р≥вн€нн€, двоелементний вектор початку ≥ к≥нц€ ≥нтервалу ≥нтегруванн€ та початкова умова.
ќстанн≥й оператор основноњ програми будуЇ граф≥к розвТ€зку у граф≥чному в≥кн≥.
Ћог≥стичне диференц≥альне р≥вн€нн€ (1) описане у файл≥ з ≥менем logeq.m. ќстанн≥й оператор цього файлу м≥стить числов≥ значенн€ двох параметр≥в лог≥стичного р≥вн€нн€ Ц r =1.5 ≥ k =2. «м≥нюючи њх значенн€, а також значенн€ початковоњ умови треба досл≥дити повед≥нку лог≥стичноњ кривоњ (2).
’≥д лабораторноњ роботи.
1. ¬ивчити теоретичну частину.
2. Ќабрати та в≥длагодити програму.
3. ќтримати лог≥стичну криву дл€ трьох значень параметра r > 0, трьох значень параметра k > 0 та трьох значень початковоњ умови X (0) > 0, зокрема X (0) < k та X (0) > k.
4. Ќаписати та захистити зв≥т.






