Цель работы: Изучение графических возможностей пакета Ms Excel. Приобретение навыков построения графика функции в трехмерном пространстве.
ПРИМЕР 4.1. Построить верхнюю часть эллипсоида  .
.
Для построения поверхности необходимо разрешить заданное уравнение относительно переменной z.
 .
.
Так как в условии речь идет о верхней части эллипсоида, то рассмотрим ОДЗ положительной части уравнения:

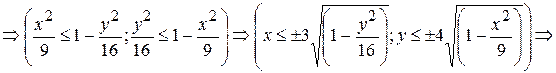
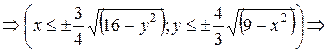

Приступим к построению поверхности. В диапазон B1:J1 введем последовательность значений переменной y: -4, -3, …,4, а в диапазон ячеек А2:А14 последовательность значений переменой x: -3, -2,5,…3.
В ячейку В2 введем формулу:
=2*(1-$A2^2/9-B$1^2/16)^0,5.
Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой – абсолютную ссылку на строку с номером, т.е. когда защищена часть адреса в ссылке, такая ссылка называется смешанной. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:J14 в них будет найдено значение z при соответствующих значениях x, y. Т.о. создается таблица значений z (рис.4.1).
Перейдем к построению поверхности.
Выделим диапазон ячеек A1:J14, содержащий таблицу значений функции и ее аргументов, вызовем Мастер диаграмм итип диаграммы Поверхность, далее заполним диалоговые окна так, как было описано в лабораторной работе № 3. После нажатия кнопки Готово получим изображение заданной поверхности (рис. 4.2).
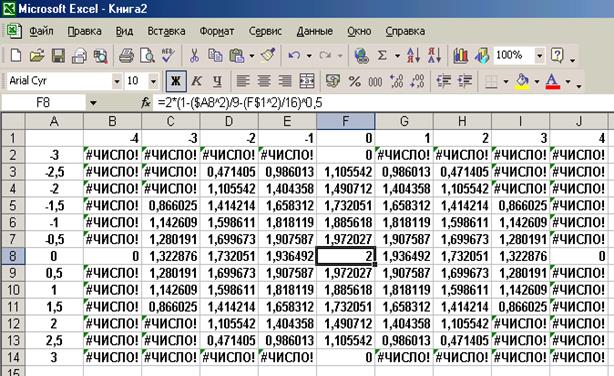
Рис.4.1

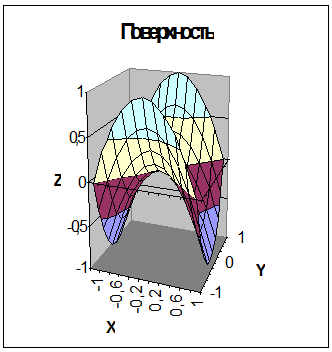
Рис.4.2 Рис. 4.3
ПРИМЕР 4.2. Построить поверхность z = x 2- y 2 при x, y Î[-1;1].
В диапазон B1:L1 введем последовательность значений переменной y, а в диапазон ячеек А2:А12 последовательность значений переменой x: -1, -0.8, …,1. В ячейку В2 введем формулу =$A2^2-B$1^2 и скопируем ее в ячейки диапазона B2:L12. На рис. 4.3. изображена з аданная поверхность.






