Стационарное поле- это поле, которое не зависит от времени в макроскопическом смысле, и зависит от времени в микроскопическом смысле,статическое поле- это поле, которое не зависит от времени как в макроскопическом, так и в микроскопическом смысле.
№3
3.3. ЭНЕРГИЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Как известно из курса физики, энергия Wэ электростатического поля, сосредоточенного в объеме V, определяется формулой (1.131). Эту формулу можно преобразовать таким образом, чтобы энергия Wэ была выражена через заряды. Заменяя вектор Е через - grad и и используя тождество div (ψа) = ψ div а + a grad ψ, где а и ψ - произвольные векторная и скалярная функции, имеющие первые производные, получаем
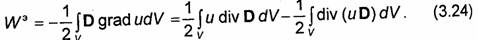
Последний интеграл в (3.24) преобразуем по теореме Остроградского-Гаусса:
где S - поверхность, ограничивающая объем V.
Предположим, что заряды, создающие электростатическое поле, сосредоточены в ограниченной области Vo, и распространим интегрирование в формуле (3.25) на все пространство. При этом поверхность S будет удалена в бесконечность, и в пределе интеграл (3.25) окажется равным нулю. Действительно, из формулы (3.9) следует, что потенциал зарядов, распределенных в ограниченной области VO на большом по сравнению с размерами областиVo расстоянии убывает пропорционально 1/r, где r- расстояние от некоторой точки внутри области V до точки наблюдения. Вектор электрического смещения D убывает как 1/r2, a поверхность S возрастает пропорционально r2.Таким образом, интеграл (3.25) при r →∞убывает как 1/r и в пределе равен нулю. Учитывая, что div D = ρ, получаем окончательное выражение для энергии электростатического поля:
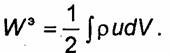(3.26)
№5
Задачи третьего типа можно решать аналитически, графически либо путем моделирования.
1.6
№3
Уравнения Максвелла (или производные от них), будучи диффе-
ренциальными уравнениями в частных производных, имеют множест-
во решений. Однако очевидно, что при полном повторении условий
эксперимента электромагнитное поле, создаваемое заданным источ-
ником, будет одинаковым. Следовательно, в каждом конкретном слу-
чае электромагнитное поле должно удовлетворять не только уравне-
ниям Максвелла, но и некоторым дополнительным условиям. На во-
прос о том, какими должны быть эти дополнительные условия, чтобы
решение электродинамической задачи было единственным, отвечает
теорема единственности. При ее доказательстве различают внутрен-
ние и внешние задачи электродинамики. Первая из них сводится к на-
хождению электромагнитного поля внутри ограниченной поверхно-
стью S области V, вторая — к нахождению электромагнитного поля
вне заданной области.
1.9
№1
Физика явления
Преломление наблюдается, когда фазовые скорости электромагнитных волн в контактирующих средах различаются (см. показатель преломления). В этом случае полное значение скорости волны должно быть разным по разные стороны границы раздела сред. Однако если проследить движение, например, гребня волны вдоль границы раздела — то соответствующая скорость должна быть одинаковой для обеих «половинок» волны (поскольку при пересечении границы максимум волны остается максимумом, и наоборот; то есть можно говорить о синхронизации падающей и прошедшей волны во всех точках границы, см. верхний рисунок). Из простого геометрического построения получаем, что скорость движения точки пересечения гребня 
с линией, наклонённой к направлению распространения волны под углом 
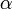, будет равна 
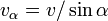, где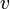 
— скорость распространения волны.
Это ясно из того, что, пока гребень волны пройдёт в направлении своего распространения (то есть перпендикулярно гребню) расстояние, равное катету треугольника, точка пересечения гребня с границей пройдёт расстояние, равное гипотенузе, а отношение этих расстояний, равное синусу угла, и есть отношение скоростей.
Тогда, приравняв скорости вдоль границы раздела для падающей и прошедшей волн, получим 
, что эквивалентно закону Снелла, поскольку показатель преломления определяется как отношение скорости электромагнитного излучения в вакууме к скорости электромагнитного излучения в среде: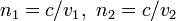 
.
В итоге на границе раздела двух сред наблюдается преломление луча, качественно состоящее в том, что углы к нормали к границе раздела сред для падающего и преломлённого луча отличаются друг от друга, то есть ход луча вместо прямого становится ломаным — луч преломляется.
Заметим, что практически тождественным способом вывода закона Снелла является построение прошедшей волны с помощью принципа Гюйгенса — Френеля (см. рисунок).
В изотропной среде для синусоидальной волны, характеризуемой частотой и волновым вектором, перпендикулярным направлению распространения волны, соображения, что составляющая волнового вектора, параллельная границе раздела, должна быть одинаковой до и после прохождения этой границы, приводят к такому же виду закона преломления.
Дополнительно стоит отметить, что волновой вектор фотона равен вектору его импульса, делённому на постоянную Планка, и это дает возможность естественной физической интерпретации закона Снелла как сохранения проекции импульса фотона на пересекаемую им границу раздела сред.
№2 
№6
