3.2.1 Проверка на наличие выбросов в пределах каждого опыта
Прежде чем приступать к дисперсионному анализу, необходимо обработать результаты измерений при каждом опыте.
Для проверки наличия статистических выбросов среди результатов измерений, полученных в условиях каждого из 
опытов для выборок малых объемов, воспользуемся критерий Романовского 
в отношении подозрительных результатов измерений.
Подозрение вызывает только два результата измерений:
- опыты, проведенные оператором 2 с использованием первого СИ за вторую смену – 29,934;
- опыты, проведенные оператором 2 с использованием второго СИ во вторую смену – 29,965.
Определим среднее значение результата измерения в пределах каждого опыта с подозрительным результатом:
Тогда для шестого и восьмого опытов среднее значение результатов измерений равно:
Стандартное отклонение результатов измерений в пределах каждого опыта с подозрительными результатами определяется по формуле:
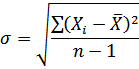
Тогда для шестого и восьмого опытов стандартное отклонение результатов измерений равно:
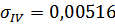
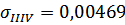
Примечание – Расчет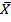 
и 
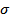осуществляется без учета подозрительного значения.
Рассчитаем критерий Романовского для шестого и восьмого опытов:
Из таблицы для 
выбираем табличное значение критерия:
Поскольку 
, то результаты не являются промахами.
3.2.2 Проверка на нормальность распределения
Из известных критериев согласия имеет место критерий Шапиро-Уилка, который используется при проверке распределения на нормальность для выборок малых объемов (не превосходящих 20), который определяется по формуле:
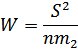
где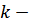 
индекс, имеющий значения от 1 до 
;
коэффициент, имеющий специальные значения для объема выборки
Таблица 2 – Результаты промежуточных расчетов в пределах первого опыта
| 
| 
|
| 29,949 | 29,947 | 0,605 |
| 29,945 | 29,945 | 0,316 |
| 29,934 | 29,943 | 0,174 |
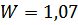
Табличное значение критерия равно 0,818. Поскольку табличное значение не превосходит рассчитанное, то гипотеза о нормальном распределении принимается.
Аналогичным образом осуществляется проверка для остальных семи опытов. И поскольку табличное значение критерия не превосходит рассчитанные значения, то гипотеза о нормальном распределении результатов измерений в пределах каждого опыта принимается.
3.2.3 Проверка на однородность дисперсий
Если в процессе проведения измерительного эксперимента использовались различное СИ, измерения выполняли различные операторы, а также измерения выполнялись в разные смены, то необходимо убедиться, что дисперсии однородны
Проверка однородности дисперсий осуществляется с помощью критерия Кохрана:
где 
наибольшее стандартное отклонение в совокупности;
стандартное отклонение в пределах каждого из 8-ми опытов.
Представим результаты промежуточных расчетов для определения критерия в таблице (результаты промежуточных расчетов представлены в таблице 3).
Таблица 3 – Результаты промежуточных расчетов
| Оператор | СИ | Смена | 
| 
|
| 29,9435 | 0,000023 | |||
| 29,9481 | 0,000019 | |||
| 29,9481 | 0,000030 | |||
| 29,9502 | 0,000036 | |||
| 29,9481 | 0,000035 | |||
| 29,9478 | 0,000033 | |||
| 29,9448 | 0,000022 | |||
| 29,9475 | 0,000029 | |||
| 
|
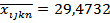
Таким образом, критерий Кохрена определяется:
Критическое значение 0,3362. Поскольку критическое значение критерия больше рассчитанного, то дисперсии, полученные в пределах каждого опыта однородны.
Критерий Фишера для определения однородности дисперсий используется для опытов с различным количеством измерений.
3.2.4 Оценивание вклада лабораторной составляющей 
Для исследования влияния всех уровней факторов на результаты измерений используется дисперсионный анализ. Поскольку измерения проводят в промежуточных условиях прецизионности с тремя изменяющимися факторами, то проведем трехфакторный дисперсионный анализ.
Трехфакторный дичперсионный анализ проведем, используя пакет Statistica. Для этого составим план эксперимента в программе (план эксперимента в пакете статистика представлен на рисунке 2).
Рисунок 2 – План эксперимента
Проведем трехфакторный дисперсионный анализ для определения вкладов от каждой составляющей 
, их попарного и тройного взаимодействия и результаты представи в виде таблица 4.
Таблица 4 – Итоговая таблица результатов дисперсионного анализа
Источник изменчивости,
| Сумма квадратов эффектов,
| Число степеней свободы,
| Средние квадраты,
|
| Оператор | 
| 
| 
|
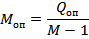
| СИ | 
| 
| 
|
| Смена |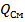 
| 
| 
|
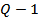
| Оператор*СИ | 
| 
| 
|
| Оператор*смена | 
| 
| 
|
| СИ*смена | 
| 
| 
|
| Оператор*СИ *смена | 
| 
| 
|
| Случайная ошибка | 
| 
| 
|
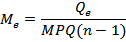
| Общая | 
| 
| 
|
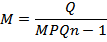
Дисперсионный анализ позволяет определить какой вклад вносит каждый изменяющийся фактор измерительной системы: оператор, СИ и смена – а также оценить вклады от взаимодействия этих факторов (результаты дисперсионного анализа представлены в таблице 5).
Таблица 5 – Результаты дисперсионного анализа
| Источник изменчивости,
| Сумма квадратов эффектов,
| Число степеней свободы,
| Средние квадраты,
|
| Оператор | 0,01028 | 
| 0,00514 |
| СИ | 0,0023 |
| 0,00115 |
| Смена | 0,0024 |
| 0,00120 |
| Оператор*СИ | 0,000252 | 
| 0,000252 |
| Оператор*смена | 0,000071 |
| 0,000071 |
| СИ*смена | 0,00011 |
| 0,00011 |
| Оператор*СИ*смена | 0,000178 |
| 0,000178 |
| Случайная ошибка | 0,006608 |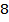 
| 0,000826 |
