Вопросы, знание которых обязательно для допуска к выполнению работы
1. Какие колебания называются гармоническими? Напишите уравнение гармонических колебаний. Поясните.
2. Что называется амплитудой, частотой, периодом, фазой и начальной фазой гармонического колебания?
3. Как связаны между собой период, частота, циклическая частота?
4. Две колеблющиеся материальные точки имеют одинаковые (разные) фазы. Что это означает?
5. Под действием каких сил происходит колебание тела на пружине в вертикальном направлении?
6. Напишите закон Гука.
7. Что называется коэффициентом жесткости пружины?
8. От каких параметров пружины зависит коэффициент жесткости?
9. Как выражаются скорость и ускорение при гармоническом колебании?
10. Что называется квазиупругой силой? Приведите примеры.
11. От чего и как зависит частота колебания тела на пружине?
12. Расскажите порядок выполнения работы.
ВВЕДЕНИЕ
Тело, подвешенное на пружине и выведенное из положения равновесия, совершает гармонические колебания.
Гармоническими называются колебания, при которых колеблющаяся величина изменяется со временем по закону синуса и косинуса.
Для механических колебаний это означает, что смещение тела х от положения равновесия происходит по закону:
х = х0 Ч sin (ωt +φ), (1)
где х0 - амплитуда (максимальное отклонение от положения равновесия);
ω= 2πν = 
- циклическая частота (ν - частота колебания; Т - период);
t - время, в течение которого совершается колебательный процесс;
φ - начальная фаза;
(ωt +φ) - фаза колебания, определяющая состояние системы в момент времени t.
Рассмотрим пружинный маятник (рис. 1), состоящий из легкой пружины, имеющей достаточно большое число витков, и тела массой m. Если оттянуть тело маятника строго вертикально вниз на небольшое 
расстояние и отпустить, то маятник начнет совершать колебания только вдоль вертикальной линии (колебания с одной степенью свободы). Колебание тела на пружине в вертикальном направлении происходит под действием двух сил: силы тяжести и упругой силы пружины. При отклонении маятника из положения равновесия будет возникать внутренняя возвращающая сила упругости, направленная к точке равновесия. Если величина отклонения маятника мала (много меньше первоначальной длины маятника), можно воспользоваться законом Гука:
F = – k×x, (2)
где k - коэффициент жесткости пружины, зависящий от ее геометрических размеров и материала, из которого она изготовлена.
По второму закону Ньютона:
F = m×a = – k×x;
.
Тогда уравнение гармонических колебаний получим в виде:
. (3)
Общее решение этого уравнения имеет вид:
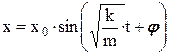. (4)
Действительно:
, (5)
. (6)
Подставляя в левую часть уравнения (3) выражение (6), а в правую - значение х из (4), приходим к тождеству, что означает правильность выбора решения в виде уравнения (4).
Из уравнений (4) и (1) следует, что циклическая частота колебаний зависит от коэффициента жесткости пружины и массы колеблющегося тела:
. (7)
Значение начальной фазы определяется в каждом конкретном случае из начальных условий.
Обобщая вывод, сделанный выше, можно утверждать, что гармонические колебания будут совершаться и при действии на тело силы любой природы, лишь бы она подчинялась уравнению (2). Силы или результирующие силы, хотя и неупругие, но подчиняющиеся уравнению (2), называются квазиупругими. Примером такой силы является результирующая двух сил (силы тяжести и силы натяжения нити), возникающая при отклонении пружинного маятника из положения равновесия.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для расчета частоты колебаний груза на пружине необходимо изменяя массу груза m определить коэффициент жесткости пружины k. Кроме того, нужно быть уверенным, что коэффициент k будет постоянным в достаточно широком диапазоне нагрузок и деформации пружины.
1. Определим k через приращение силы ΔF и приращение смещения Δx:
k =ΔF/Δx.
Для этого на чашечку, подвешенную к пружине, следует класть гирьки так, чтобы нагрузка увеличивалась каждый раз на 20 г, и, соответственно, производить отсчет xi положений чашечки и пружины.
По разности xi до и после нагрузки определяют Δx для соответствующей нагрузки: ΔF = Δmg.
Δxi=|xi - xi-1|
Чтобы убедиться, что не произошло неупругих деформаций пружины, необходимо произвести отсчеты и при уменьшающейся нагрузке. Если при разных нагрузках значения коэффициента k в пределах погрешности получаются одинаковыми, то закон Гука выполняется во всем диапазоне нагрузок. В этом случае можно определить среднее значение k.
2. По формуле (7) рассчитать циклическую частоту ω (при расчете обратите внимание на систему единиц). Результаты измерений занесите в таблицу, определите относительную и абсолютную погрешности w.
Таблица
| № п/п | m, кг | xi, м | Δxi, м | k, H/м | w, рад/c | wў, рад/c |
| 0.02 | ||||||
| 0.04 | ||||||
| 0.06 | ||||||
| 0.08 | ||||||
| 0.10 | ||||||
| 0.12 | ||||||
| 0.10 | ||||||
| 0.08 | ||||||
| 0.06 | ||||||
| 0.04 | ||||||
| 0.02 | ||||||
| Среднее значение |
3. Необходимо экспериментально проверить рассчитанную циклическую частоту ωў. Для этого с помощью секундомера определяют время t числа N полных колебаний, откуда
Опыт выполняется следующим образом.
На чашечке устанавливают груз m=0,1 кг, для которого по формуле (7) был произведен расчет w.
Слегка оттянув чашечку (строго вертикально вниз), приводят груз в колебание.
Измерение времени не рекомендуется начинать с момента запуска. После нескольких качаний, усвоив темп счета, запускают секундомер в момент, когда груз занимает крайнее нижнее положение (либо крайнее верхнее). В момент запуска секундомера начинают счет колебаний с цифры "ноль" (а не "один"). Для одного и того же числа полных колебаний N (N і 20) определяют время колебаний t не менее трех раз. При этом не обязательно каждый раз останавливать чашечку с грузом, а затем снова ее запускать.
Расхождение в измеренных промежутках времени не должно сильно превышать погрешность секундомера (Dt = 0.2 с). Кроме того, если обнаружится расхождение во времени t больше, чем t /N, это означает, что при подсчете числа колебаний допущен просчет.
По измеренным t найти tср. Используя tсp и число полных колебаний N, определите Т и ωў.
6. Сравните результаты для w и w' с учетом их абсолютных погрешностей для m=0,1 кг.
7. Рассчитайте массу чашечки. Поясните, как вы это сделали.
Рекомендуемая литература
1. Савельев И.В. Курс общей физики. T. I. - Киев: Наука, 1977. § 14, 49, 50, 53, 54.
2. Архангельский М.В. Курс физики: механика. - М.: Просвещение, 1975. С. 62-72, 224-237, 297-305.
3. Грабовский Р.И. Курс физики. - М.: Высшая школа, 1970. § 10, 27, 29.
4. Ландсберг Г.С. Элементарный учебник физики. T. I. - М.: Наука, 1967. § 58, 59, 60, 61. С. 277-287.
5. Мэрион Дж.Б. Общая физика с биологическими примерами. - М.: Высшая школа, 1986.
6. Кац Ц.Б. Биофизика на уроках физики. - М.: Просвещение, 1988.
