Функциональная зависимость атрибутов отношения напоминает понятие функциональной зависимости в математике. Но это не одно и то же. Для сравнения напомним математическое понятие функциональной зависимости:
Определение 2. Функциональная зависимость (функция) - это тройка объектов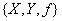 
, где
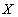- множество (область определения),
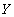- множество (множество значений),
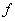- правило, согласно которому каждому элементу 
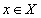ставится в соответствие один и только один элемент 
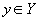(правило функциональной зависимости).
Функциональная зависимость обычно обозначается как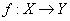 
или 
.
Замечание. Правило 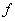может быть задано любым способом - в виде формулы (чаще всего), при помощи таблицы значений, при помощи графика, текстовым описанием и т.д.
Функциональная зависимость атрибутов отношения тоже напоминает это определение. Действительно:
- В качестве области определения выступает домен, на котором определен атрибут 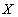(или декартово произведение доменов, если 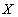является множеством атрибутов)
- В качестве множества значений выступает домен, на котором определен атрибут 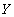(или декартово произведение доменов)
- Правило 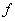реализуется следующим алгоритмом - 1) по данному значению атрибута 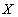найти любой кортеж отношения, содержащий это значение, 2) значение атрибута 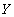в этом кортеже и будет значением функциональной зависимости, соответствующим данному 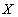. Определение функциональной зависимости в отношении гарантирует, что найденное значение 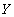не зависит от выбора кортежа, поэтому правило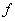
определено корректно.
Отличие от математического понятия отношения состоит в том, что, если рассматривать математическое понятие функции, то для фиксированного значения 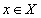соответствующее значение функции всегда одно и то же. Например, если задана функция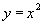 
, то для значения 
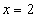соответствующее значение 
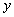всегда будет равно 4. В противоположность этому в отношениях значение зависимого атрибута может принимать различные значения в различных состояниях базы данных. Например, атрибут ФАМ функционально зависит от атрибута Н_СОТР. Предположим, что сейчас сотрудник с табельным номером 1 имеет фамилию Иванов, т.е. при значении детерминанта равного 1, значение зависимого аргумента равно "Иванов". Но сотрудник может сменить фамилию, например на "Сидоров". Теперь при том же значении детерминанта, равного 1, значение зависимого аргумента равно "Сидоров".
Таким образом, понятие функциональной зависимости атрибутов нельзя считать полностью эквивалентным математическому понятию функциональной зависимости, т.к. значение этой зависимости различны при разных состояниях отношения, и, самое главное, эти значения могут меняться непредсказуемо.
Функциональная зависимость атрибутов утверждает лишь то, что для каждого конкретного состояния базы данных по значению одного атрибута (детерминанта) можно однозначно определить значение другого атрибута (зависимой части). Но конкретные значение зависимой части могут быть различны в различных состояниях базы данных.
2НФ (Вторая Нормальная Форма)
Определение 3. Отношение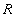 
находится во второй нормальной форме (2НФ) тогда и только тогда, когда отношение находится в 1НФ и нет неключевых атрибутов, зависящих от части сложного ключа. (Неключевой атрибут - это атрибут, не входящий в состав никакого потенциального ключа).
Замечание. Если потенциальный ключ отношения является простым, то отношение автоматически находится в 2НФ.
Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ не находится в 2НФ, т.к. есть атрибуты, зависящие от части сложного ключа:
Зависимость атрибутов, характеризующих сотрудника от табельного номера сотрудника является зависимостью от части сложного ключа:
