(Краткие теоретические сведения)
Энергия взаимодействия точечных зарядов
Энергия взаимодействия системы точечных зарядов равна работе внешних сил по созданию данной системы (см. рис.1) посредством медленного (квазистатического) перемещения зарядов из бесконечно удаленных друг от друга точек в заданные положения. Эта энергия зависит только от конечной конфигурации системы, но не от способа, каким эта система была создана.
|
| Рис.1 |
Основываясь на таком определении, можно получить следующую формулу для энергии взаимодействия двух точечных зарядов, расположенных в вакууме на расстоянии r 12 друг от друга:
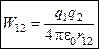. (1)
Если система содержит три неподвижных точечных заряда, то энергия их взаимодействия равна сумме энергий всех парных взаимодействий:
,
где r 12 – расстояние между первым и вторым, r 13 - между первым и третьим, r 23 – между вторым и третьим зарядами. Аналогично вычисляется электрическая энергия взаимодействия системы из N точечных зарядов:
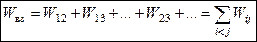. (2)
Например, для системы из 4-х зарядов формула (2) содержит 6 слагаемых.
Электрическая энергия заряженных проводников
Электрическая энергия уединенного заряженного проводника равна работе, которую нужно совершить, чтобы нанести на проводник данный заряд, медленно перемещая его бесконечно малыми порциями из бесконечности, где изначально эти порции заряда не взаимодействовали. Электрическую энергию уединенного проводника можно вычислить по формуле
, (3)
где q – заряд проводника, j - его потенциал. В частности, если заряженный проводник имеет форму шара и расположен в вакууме, то его потенциал 
и, как следует из (3), электрическая энергия равна
,
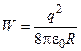где R – радиус шара, q – его заряд.
Аналогично определяется электрическая энергия нескольких заряженных проводников – она равна работе внешних сил по нанесению данных зарядов на проводники. Для электрической энергии системы из N заряженных проводников можно получить формулу:
, (4)
где 
и 
- заряд и потенциал 
-го проводника. Заметим, что формулы (3), (4) справедливы и в том случае, когда заряженные проводники находятся не в вакууме, а в изотропном нейтральном диэлектрике.
При помощи (4) вычислим электрическую энергию заряженного конденсатора. Обозначив заряд положительной обкладки q, ее потенциал j1, а потенциал отрицательной обкладки j2, получим:
,
где 
- напряжение на конденсаторе. Учитывая, что 
, формулу для энергии конденсатора можно представить также в виде
, (5)
где C – емкость конденсатора.
Собственная электрическая энергия и энергия взаимодействия
Рассмотрим электрическую энергию двух проводящих шаров, радиусы которых R 1, R 2, а заряды q 1, q 2. Будем считать, что шары расположены в вакууме на большом по сравнению с их радиусами расстоянии l друг от друга. В этом случае расстояние от центра одного шара до любой точки поверхности другого примерно равно l и потенциалы шаров можно выразить формулами:
, 
.
Электрическую энергию системы найдем при помощи (4):
.
Первое слагаемое в полученной формуле – энергия взаимодействия зарядов, расположенных на первом шаре. Эту энергию называют собственной электрической энергией (первого шара). Аналогично, второе слагаемое – собственная электрическая энергия второго шара. Последнее слагаемое – энергия взаимодействия зарядов первого шара с зарядами второго.
При 
электрическая энергия взаимодействия существенно меньше суммы собственных энергий шаров, однако при изменении расстояния между шарами собственные энергии остаются практически постоянными и изменение полной электрической энергии примерно равно изменению энергии взаимодействия. Этот вывод справедлив не только для проводящих шаров, но и для заряженных тел произвольной формы, расположенных на большом расстоянии друг от друга: приращение электрической энергии системы равно приращению энергии взаимодействия заряженных тел системы: 
. Энергия взаимодействия 
удаленных друг от друга тел не зависит от их формы и определяется формулой (2).
При выводе формул (1), (2) каждый из точечных зарядов рассматривался как нечто целое и неизменное. Учитывалась только работа, совершаемая при сближении таких неизменных зарядов, но не на их образование. Напротив, при выводе формул (3), (4) учитывалась также работа, совершаемая при нанесении зарядов qi на каждое из тел системы путем переноса электричества бесконечно малыми порциями из бесконечно удаленных точек. Поэтому формулы (3), (4) определяют полную электрическую энергию системы зарядов, а формулы (1), (2) только электрическую энергию взаимодействия точечных зарядов.
Объемная плотность энергии электрического поля
Электрическую энергию плоского конденсатора можно выразить через напряженность поля между его обкладками:
,
где 
- объем пространства, занятого полем, S – площадь обкладок, d – расстояние между ними. Оказывается, через напряженность можно выразить электрическую энергию и произвольной системы заряженных проводников и диэлектриков:
, (5)
где
,
а интегрирование проводится по всему пространству, занятому полем (предполагается, что диэлектрик изотропный и 
). Величина w представляет собой электрическую энергию, приходящуюся на единицу объема. Вид формулы (5) дает основания предположить, что электрическая энергия заключена не во взаимодействующих зарядах, а в их электрическом поле, заполняющем пространство. В рамках электростатики это предположение проверить экспериментально или обосновать теоретически невозможно, однако рассмотрение переменных электрических и магнитных полей позволяет удостоверится в правильности такой полевой интерпретации формулы (5).
