Решение. 1. Ось у, направим вверх, поместив ее начало в нижней точке траектории аэростата

1. Ось у, направим вверх, поместив ее начало в нижней точке траектории аэростата. При падении на аэростат действуют силы тяжести G = тg, сила сопротивления воздуха R и подъемная сила Т (рис. 121). Аэростат принимаем за материальную точку.

2. Составляем дифференциальное уравнение движения:

 

.

 

3. Дважды интегрируем уравнение движения. Для постоянных сил
интеграл берется просто:

 

 

Начальные условия: t = 0, у = Н, . Отсюда находим константы интегрирования С ₁ = mv ₀, C ₂ = тН. Получаем уравнения

 

, (1)

. (2)

 

Аналогично составляем уравнение при подъеме аэростата.

 

Рис. 121 Рис. 122

 

Сила сопротивления при этом меняет свое направление (рис. 122). Оставляя ось у прежней, время отсчитываем от нуля с момента подъема:

 

Интегрируя уравнение

 

, (3)

получаем

. (4)

 

Начальные условия: t = 0, у = 0, . Находим константы интегрирования: С ₃ = 0, С ₂= 0. Из (4) следует

 

. (5)

 

4. Находим искомое время падения. Обозначаем его за t ₁, а время подъема — за t ₂. По условию t ₁ + t ₂ = t ₀. Подставляем в (1,2) условия: t = t ₁, , у = 0, а в (5) t = t ₂, у = Н. Получаем систему трех уравнений с неизвестными t ₁, Н, v ₀:

(6)

, (7)

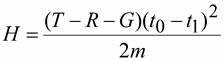. (8)

 

Исключая неизвестную высоту Н и неизвестную начальную скорость v ₀, получаем

.