Гравитационное взаимодействие играет в природе важную роль, оно присуще всем телам и определяется только массами тел. Закон гравитации (всемирного тяготения) установлен И. Ньютоном:
,
или в векторной форме 
где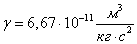 
– гравитационная постоянная,
r – расстояние между центрами масс тел, 
– единичный вектор нормали.
Малая величина γ указывает на то, что гравитационное взаимодействие может быть значительным только в случае больших масс или малых расстояний.
Движение тел массой m только под действием сил тяготения называется свободным падением с ускорением свободного падения g. Величина gобычно рассматривается для массивных тел массой М (звезд, планет, спутников) и может быть определена по уравнению:
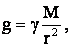
где М – масса массивного тела,
r – расстояние от центра масс массивного тела до рассматриваемой точки.
В частном случае, для Земли (если пренебречь суточным вращением Земли вокруг своей оси):
,
где r – расстояние от центра Земли до рассматриваемой т. А.
Если учесть, что Земля имеет форму не шара, а трехосного эллипсоида вращения (шар сплюснутый у полюсов), то
Первую космическую скорость v1 можно рассчитать, если учесть, что притяжение Земли выполняет роль силы, удерживающей спутники на круговой орбите (центростремительной силы 
):
Силы в природе и их проявление:
а) вес тела 
– сила, с которой тело вследствие тяготения к Земле действует на опору (или подвес), удерживающую тело от свободного падения:
б) невесомость – состояние тела, при котором оно движется только под действием силы тяжести 
с ускорением равным ускорению свободного падения 
в данной точке;
в) перегрузки – состояние тела, при котором оно движется с ускорением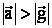 
;
г) сила упругости 
– возникает в телах при деформации и обусловлена взаимодействием атомов тела.
Деформация – изменение формы и размеров тел под действием внешних сил.
Деформации бывают:
1) пластические – когда форма и размеры тел не восстанавливаются после прекращения действия внешних сил;
2) упругие – после прекращения действия внешних сил тело принимает первоначальную форму и размер.
Виды деформаций:
1) растяжение или сжатие;
2) изгиб;
3) кручение;
4) сдвиг;
5) срез;
Основные характеристики деформации (на примере деформации растяжения стержня):
Закон Гука, справедливый только для упругой деформации, можно сформулировать двояко:
а) относительная деформация ε прямо пропорциональна напряжению σ:
σ = Е ε,
где Е – модуль Юнга (определяется напряжением, при котором относительное удлинение равно единице).
б) абсолютная деформация тела ∆Х при упругой деформации прямо пропорциональна действующей на тело силе F:
F = k∆Х (или Fупр = –kХ),
где k – коэффициент упругости (жесткости);
в) силы трения возникают между телами, соприкасающимися друг с другом и находящимися:
в покое – сила трения покоя Fтр. пок:
Fтр. пок. = µ0 N,
где µ0 – коэффициент трения покоя,
N – сила нормального давления;
движущимися относительно друг друга – сила трения скольжения Fтр:
Fтр = µ N,
где µ – коэффициент трения скольжения (зависит от природы и состояния поверхностей скольжения и не зависит от площади соприкасающихся поверхностей),
N – сила нормального давления.
Сила трения направлена вдоль поверхности соприкосновения тел против направления движения (действующей внешней силе) и в результате ее действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел;
г) если на материальную частицу (тело) в каждой точке пространства действуют определенные силы, то эту совокупность сил называют силовым полем. Если силы поля постоянные по величине, неизменны по направлению и не зависят от времени, то образуемые ими поля называются однородными или постоянными силовыми полями.
Момент силы – произведение силы 
на плечо d:
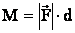
Плечо силы – кратчайшее расстояние от оси вращения О до направления действия силы, т.е. длина перпендикуляра, опущенного из оси О на направление действия силы:
d1 – плечо силы F1,
d2 – плечо силы F2.
Из рисунка видно, что плечо 
. Тогда момент силы М можно записать:
,
или в векторной форме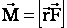 
.
Для вращательного движения – угловое ускорение 
, получаемое телом (материальной точкой), прямо пропорционально результирующему моменту приложенных сил 
и обратно пропорционально моменту инерции тела (материальной точки):
где J – момент инерции тела (материальной точки).
Для вращательного движения – тело, способное вращаться вокруг неподвижной оси, будет находиться в покое или вращаться равномерно, если алгебраическая сумма моментов приложенных сил относительно оси вращения равна нулю:
Для вращательного движения – вращательные моменты равны по величине и противоположны по направлению:
Задача №1. Под действием силы тяги F, направленной вдоль горизонтальной плоскости, по ее поверхности начинает скользить без начальной скорости тело массой 4 кг и через 3 с после начала движения приобретает скорость 0,6 м/с. Найти силу F, если коэффициент трения между телом и плоскостью 0,2.
| v0 = 0; m = 4 кг; t = 3 c; v = 0,6 м/с; k = 0,2. | 
|
| F –? |
Решение: на движущееся тело действует четыре силы: сила тяги , сила трения 
, сила тяжести и сила нормальной реакции 
плоскости. Вектор 
направлен параллельно плоскости вправо. Запишем для данного тела уравнение второго закона Ньютона в векторной форме:
(1)
За положительное направление оси Х примем направление движения тела, ось У направим вертикально вверх. Спроецировав все силы на ось Х, составим уравнение движения тела:
Отсюда 
Найдя проекции сил на ось У, запишем уравнение (1) в проекции на эту ось:
;
Учитывая, что 
,
получим 
(2)
Так как тело двигалось равноускоренно без начальной скорости, то в момент времени t скорость тела:
.
Отсюда находим: 
(3)
Подставив значения Fтр и а из формул (2) и (3) в формулу (1), найдем:
.
Проверим размерность:
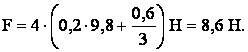
Ответ: сила тяги равна F = 8,6 Н.
Задача №2. Груз массой 45 кг перемещается по горизонтальной плоскости под действием силы 294 Н, направленной под углом 30о к горизонту. Коэффициент трения груза о плоскость 0,1. Определить величину ускорения груза.
| F = 294 H; m = 45 кг; k = 0,1; α = 30о. |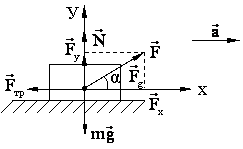 
|
| а –? |
Решение: на груз действуют: – сила тяжести; – сила нормальной реакции плоскости; – сила тяги; – сила трения. Вектор направлен параллельно плоскости направо. Запишем для данного тела уравнение второго закона Ньютона в векторной форме:
(1)
Выбрав за положительное направление оси Х направление движения тела, а ось У направив вертикально вверх, и, найдя проекции сил на оси, запишем уравнение (1) в проекциях на эти оси:
(2)
(3)
Из уравнения (3) находим, что
.
Тогда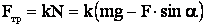 
.
Подставим это выражение в (2) получим:
,
откуда 
Ответ: груз перемещается с ускорением 
Задача №3. На гладком столе лежат два связанных нитью груза массами 0,2 кг и 0,3 кг. К ним приложены силы 0,6 Н и 1 Н соответственно, линии действия которых совпадают с нитью. С каким ускорением движутся грузы? Чему равно натяжение нити? Трение не учитывать.
| F1 = 0,6 H; F2 = 1,0 H; m1 = 0,2 кг; m2 = 0,3 кг. | 
|
| а, Т –? |
Решение: рассмотрим силы, действующие на каждый груз.
На первый груз действуют: 
– сила тяжести, 
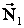– сила нормальной реакции; 
– сила натяжения нити, 
– приложенная сила. Уравнение движения для первого груза:
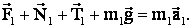
Проецируя векторное уравнение второго закона Ньютона для первого груза на оси 0Х и 0У, получаем:
(1)
На второй груз действуют силы: 
– сила тяжести, 
– сила нормальной реакции;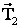 
– сила натяжения нити, 
– приложенная сила.
Запишем второй закон Ньютона для второго груза в проекциях на те же оси:
(2)
Складывая уравнения (1) и (2) и учитывая, что для невесомой и нерастяжимой нити:
Т1 = Т2 = Т,
а1 = а2 = а
получим 
отсюда 
м/с2.
Из уравнения (1): 
Н.
Ответ: ускорение, с которым движется система грузов равно а = 0,8 м/с2; сила натяжения нити Т = 0,76 Н
Задача №4. Брусок массой 2 кг скользит по горизонтальной поверхности под действием груза массой 0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через неподвижный блок. Коэффициент трения бруска о поверхность 0,1. Найти ускорение движения тела и силу натяжения нити. Массами блока и нити, а также трением в блоке пренебречь.
| m1 = 2 кг; m2 = 0,5 кг; k = 0,1. | 
|
| а1, Т –? |
Решение: рассмотрим движение каждого груза отдельно. На брусок действуют: – сила тяжести; – сила нормальной реакции плоскости; 
– сила натяжения нити; – сила трения.
Запишем для бруска уравнение второго закона Ньютона в векторной форме:
Спроецировав полученное уравнение на выбранные направления осей 0Х и 0У, получим: 
(1)
(2)
Поскольку из уравнения (2) следует, что 
, то
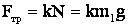
Тогда уравнение примет вид:
(3)
На груз действуют: – сила тяжести; 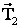– сила натяжения нити. Запишем для груза уравнение второго закона Ньютона в векторной форме:
(4)
Спроецировав уравнение (4) на ось 0У, получим:
(5)
Решая совместно систему уравнений (3) и (5) методом почленного сложения уравнений и учитывая, что Т1 = Т2 = Т и а1 = а2 = а, получаем:
откуда 
Силу натяжения нити находим из уравнения (5):
Ответ: ускорение блока а = 1,2 м/с2; сила натяжения нити Т ≈ 4,3 Н.
Задача №5. По наклонной плоскости с углом наклона 300 скользит вниз брусок. Найти его ускорение, если коэффициент трения бруска о плоскость равен 0,8.
| α = 300; k = 0,4. |
| а1 –? |
Решение: на тело при его скольжении по наклонной плоскости действуют: – сила тяжести; – сила нормальной реакции плоскости; – сила трения.
Запишем для тела уравнение второго закона Ньютона в векторной форме:
Направим ось Х вдоль наклонной плоскости вниз, а ось У перпендикулярно плоскости вверх.
Найдем проекции сил на выбранные направления осей Х и У и запишем скалярные уравнения движения относительно этих осей:
; (1)
(2)
Из уравнения (2) находим, что
.
Учитывая, что 
, запишем уравнение (1) в виде:
,
откуда 
м/с2≈1,6 м/с2
В частности, при отсутствии трения (k = 0):
a = gsinα;
а = 9,8·0,5 = 4,9 м/с2.
Ответ: брусок скользит вниз с ускорением а = 1,6 м/с2.
Задача №6. Груз массой 5 кг движется вверх по наклонной плоскости под действием связанного с ним невесомой и нерастяжимой нитью груза массой 2 кг. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость 0,1, угол наклона плоскости 360. Определить ускорение, с которым движется тело, и силу натяжения нити. Массами нитей, блока, а также трением в блоке пренебречь.
| m1 = 5 кг; m2 = 2 кг; k = 0,1; α = 360. | 
|
| а, Т –? |
Решение. Рассмотрим движение каждого груза отдельно. На первый груз действуют: – сила тяжести; – сила нормальной реакции наклонной плоскости; – сила натяжения нити; – сила трения.
По условию задачи вектор ускорения для первого груза направлен вверх по наклонной плоскости. Запишем для первого груза уравнение второго закона Ньютона в векторной форме:
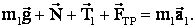(1)
Направим ось Х вверх по наклонной плоскости, ось У1 – перпендикулярно к ней. Проецируя уравнение (1) на выбранные направления осей Х и У1, получаем:
(2)
(3)
Из уравнения (3) находим, что , поэтому
(4)
Подставляя выражение (4) в уравнение (2), получаем:
(5)
На второй груз действуют: – сила тяжести; 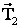– сила натяжения нити. Ускорение 
второго груза направлено вертикально вниз. Запишем уравнение второго закона Ньютона в векторной форме для второго груза:
(6)
Ось У2 направим вертикально вниз. Спроецировав уравнение (6) на ось У2, получим:
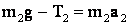(7)
Сложив почленно уравнения (5) и (7), получим:
Учитывая, что Т1 = Т2 = Т и а1 = а2 = а, находим:
;
Силу натяжения нити определим из уравнения (7):
;
Ответ: ускорение движения тела а = –1,93 м/с2; сила натяжения нити Т = 15,74 Н. Полученные ответы справедливы только в том случае, если телоm1 двигалось вверх по наклонной плоскости. Если же в начальный момент тела были неподвижны или двигались в противоположном направлении, задачу следует переделать, так как направление силы трения при таком движении изменяется на противоположное.
Задача №7. Груз массой 100 г, привязанный на невесомой нити длиной 50 см, движется в вертикальной плоскости с постоянной скоростью 5 м/с. Определить натяжение нити при прохождении грузом нижней и верхней точек траектории. Чему равна разность сил натяжения в этих точках? Как она зависит от скорости движения груза?
| m = 100 г = 0,1 кг; ℓ = 50 см = 0,5 м; v = 5 м/с; g = 9,8 м/с2. | 
|
| Т1, Т2, ∆Т = Т1 – Т2 –? |
Решение: на груз действуют две силы: сила тяжести и сила натяжения нити. Величина и направление силы тяжести не зависят от положения груза, а величина и направление силы натяжения изменяются при движении. Рассмотрим каждый случай отдельно.
1-ый случай (рис. а): тело находится в нижней точки траектории. Сила тяжести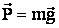 
направлена вертикально вниз, сила натяжения вертикально вверх, и обе направлены перпендикулярно к скорости, следовательно и результирующая сила также перпендикулярна скорости и создаёт только нормальное ускорений 
. Запишем уравнение второго закона Ньютона в векторной форме:
Направим ось У по радиусу к центру окружности и запишем второй закон Ньютона в проекции на это направление:
где 
тогда 
откуда 
2-ой случай (рис. б): тело находится в верхней точке траектории. В этом случае обе силы и сила 
тяжести и сила натяжения 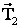, направлены вниз и обе, как и в 1 случае, перпендикулярны к скорости. Запишем второй закон Ньютона в векторной форме:
.
Направим ось У опять по радиусу к центру окружности и запишем второй закон Ньютона в проекции на эту ось:
,
где
откуда 
определим 
Ответ: Т1 = 6 Н; Т2 = 4 Н; Т = 2 Н.
Задача №8. С каким ускорением надо поднимать груз на веревке, чтобы сила натяжения веревки была в 2 раза больше силы тяжести груза?
Решение: на груз действуют две силы: сила тяжести груза и сила реакции каната 
, численно равная по третьему закону Ньютона силе его натяжения (Тнат = Т). Эти силы направлены в противоположные стороны, причем Т > Р (груз движется вверх). Силы и , действуя на тело, сообщают ему ускорение, поэтому их равнодействующая определится по второму закону. Запишем векторное уравнение:
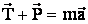
Абсолютное значение ускорения найдем из соотношения, записанного в проекциях на координатную ось ОХ
или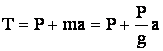 
По условию данной задачи сила натяжения веревки Т = 2Р, следовательно:
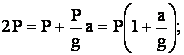
Ответ: с ускорением равному ускорению свободного падения a = g.
Задача №9. Две гири весом Р1 = 3 кг и Р2 = 5 кг соединены нерастяжимой невесомой нитью и перекинуты через неподвижный блок. Определить ускорение, с которым движутся гири и натяжение нити.
| Р1 = 3 кг; Р2 = 5 кг. | 
|
| а, Т –? |
Решение: оба груза движутся с одним и тем же ускорением . На каждый груз действуют две силы: сила тяжести 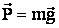, появляющаяся в результате взаимодействия этого груза с Землей и сила реакции нити , численно равная силе натяжения нити , т.е. 
или 
.
Уравнение движения грузов в проекциях сил на ось ОХ имеет вид:
для первого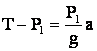 
(1)
для второго 
(2)
Решая систему уравнений, получаем:
1) 
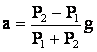или 
(3)
Все данные выражаем в СИ: Р1 = 3 кг = 3·9,8 Н;
Р2 = 5 кг = 5·9,8 Н;
Получаем 
2) в формулу (1) или (2) подставим значение ускорения и определим силу натяжения нити:
Ответ: ускорение движения гирь a = 2,45 м/с2; сила натяжения нити T = 36,75 Н.
Задача №10. Определить силу давления груза весом на пол кабины лифта, движущегося равноускоренно с ускорением : при движении лифта вверх и при движении вниз.
Решение: на груз действуют силы тяжести и сила реакции пола , численно равная силе давления груза на пол лифта (по третьему закону Ньютона):
а) при движении лифта вверх уравнение движения согласно второму закону Ньютона будет иметь вид (рис а) в векторной форме:
(1)
Абсолютное значение TI найдем из уравнения (1) в проекциях сил на ось ОХ:
,
отсюда 
При движении лифта вверх с ускорением, направленным вверх, сила давления груза на пол кабины больше вела.
б) при движении лифта вниз (рис б):
,
,
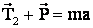При движении лифта вниз с ускорением, направленным вниз, сила давления груза на пол кабины меньше его веса.
Задача №11. Автомобиль весом движется с постоянной скоростью v:
а) по плоскому горизонтальному мосту; б) по выпуклому мосту; в) по вогнутому мосту.
Радиус кривизны моста в двух последних случаях равен R.
Какое давление оказывает на мост автомобиль (в каждом случае), проезжая через середину моста?
Решение: в вертикальном направлении на автомобиль действуют две силы: сила тяжести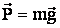 
и вверх сила реакции моста (равная по третьему закону Ньютона силе давления автомобиля на мост).
1) Когда автомобиль едет по горизонтальной поверхности, он не испытывает никаких ускорений в вертикальном направлении. Это означает, что равнодействующая двух сил и равна нулю, т.е.
или 
,
отсюда 
.
Таким образом на плоский горизонтальный мост автомобиль давит с силой, равной весу.
2) Когда автомобиль движется по выпуклому мосту, то он испытывает нормальное или центростремительное ускорение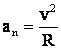 
, направленное вниз, к центру кривизны моста и по второму закону Ньютона центростремительная сила, очевидно, есть равнодействующая двух действующих сил и :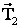
,
или 
Таким образом: 
,
т.е. давление, оказываемое автомобилем на мост, меньше его веса.
3) При движении по вогнутому мосту испытываемое автомобилем центростремительное ускорение 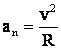направлено вверх:
Таким образом: 
,
т.е. давление, оказываемое на мост, больше веса автомобиля.
Задача №12. Ведерко с водой, укрепленное на веревке, вращают в вертикальной плоскости. С какой наименьшей частотой нужно его вращать, чтобы при прохождении через верхнюю точку траектории удержать воду в ведерке? Расстояние от центра вращения до дна ведерка равно0,5 м.
| ℓ = 0,5 м; g = 9,8 м/с2. | 
|
| n –? |
Решение: при движении воды в ведерке на нее действуют две силы: сила тяжести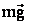 
и сила реакции со стороны дна веревка . При прохождении верхней точки траектории обе эти силы направлены вертикально вниз. Запишем второй закон Ньютона в векторном виде:
Так как каждая сила перпендикулярна к скорости, то результирующая этих сил создает только нормальное ускорение. Направим ось У по радиусу к центру и запишем второй закон в проекции на эту ось:
,
где 
При больших скоростях вращения (больших частотах обращения) N >> mg, при уменьшении частоты обращения N уменьшается и в предельном случае обращается в ноль, поэтому второй закон Ньютона для этого предельного случая будет иметь вид:
;
;
;
Ответ: частота вращения равна n = 0,7 об/с.
Задача №13. Математический маятник массой 500 г и длиной 1 м равномерно вращается в вертикальной плоскости со скоростью 1,5 м/с. Определить натяжение нити в тот момент, когда она образует с вертикалью угол 600. Чему равно в этот момент тангенциальное (касательное) ускорение?
| m = 500 г = 0,5 кг; ℓ = 1 м; α = 600; g = 9,8 м/с2. | 
|
| FH, aτ –? |
Решение: на маятник действуют две силы: сила тяжести , направленная вертикально вниз, и сила натяжения 
, направленная по радиусу к центру окружности.
Выбираем координатные оси: Х – по направлению касательной к траектории; У – по радиусу к центру.
Раскладываем силу тяжести на составляющие по этим направлениям:
Сила натяжения имеет только одну составляющую по оси У:
.
Запишем второй закон Ньютона в проекциях на выбранные направления:
на ось Х: 
;
;
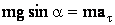м/с2;
на ось У: 
;
;
Ответ: сила натяжения нити FH = 3,58 Н; касательное ускорение aτ = 8,50 м/с2.
Задача №14. Камень соскальзывает с полусферы радиуса R. В момент, когда угол, образованный радиусом, проведенным в точку, где находится камень, и вертикалью равен α, скорость камня равна v. Масса камня m, коэффициент трения камня о сферу k. Найти давление камня на сферу и его тангенциальное ускорение.
| m; v; α; k; r. | 
|
| Fg, aτ –? |
Решение: на камень при его движении действуют три силы: сила тяжести , направленная вертикально вниз; сила реакции полусферы , направленная по продолжению радиуса ОА, и сила трения , направленная по касательной к траектории, т.е. перпендикулярно радиусу ОА. Выберем направление координатных осей следующим образом: ось Х по касательной к окружности в сторону, совпадающую со скоростью движения; ось У по радиусу к центру окружности. Разложим силу тяжести по этим направлениям:
;
.
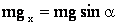Запишем второй закон Ньютона в проекциях на эти направления:
на ось Х: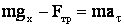 
; (1)
на ось У: 
;
где 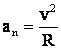, следовательно,
.
По третьему закону Ньютона:
Теперь определим 
из уравнения (1) найдем aτ:
Ответ: 
; 
.
Задача №15. Найти численное значение первой космической скорости тела, брошенного с Земли (сопротивлением воздуха пренебречь).
Решение: при сообщении телу некоторой определенной скорости в горизонтальном направлении тело будет двигаться вокруг Земли по круговой орбите, превратившись в искусственный спутник Земли. Соответствующее значение скорости носит название первой космической скорости. В рассматриваемом случае на тело действует только сила взаимодействия с Землей и выражается формулой (закон всемирного тяготения):
, (1)
где МЗ – масса Земли,
m – масса тела,
γ – гравитационная постоянная,
R – расстояние тела от центра Земли (равное радиусу кривизны траектории),
R = RЗ + h.
Очевидно, эта сила и будет сообщать телу центростремительное (нормальное) ускорение 
, изменяющее направление скорости. По второму закону Ньютона:
;
в данном случае: 
(2)
Приравнивая два выражения (1) и (2), находим скорость:
;
Подставим в эту формулу численные значения входящих в него величин (выражаем в единицах системы СИ):
γ = 6,67·10-11 Н·м2·кг-2,
МЗ = 6·1024 кг.
R = RЗемли = 6,37·106 м
(допускаем, что тело находится на некоторой очень малой высоте над поверхностью Земли, т.е. h << RЗемли).
Выполняя арифметические действия, находим:
Ответ: первая космическая скорость равна 7,9·103 м/с.
Задача №16. Наибольшее удаление от земной поверхности первого искусственного спутника Земли равнялось h = 947 км. Какой скоростью должен был обладать спутник на этой высоте, чтобы удержаться на круговой орбите? Каков при этом период обращения спутника вокруг Земли? Сопротивлением атмосферы движению пренебречь. Ускорение силы тяжести на поверхности Земли принять равным g = 9,8 м/с2, а радиус Земли RЗ =6370 км.
| h = 947 км; g = 9,8 м/с2; RЗ = 6370 км. |
| v, Т –? |
Решение: на спутник действует только сила притяжения к Земле, которая сообщает спутнику центростремительное ускорение.
Поэтому выполняется равенство
где m – масса спутника,
R = (R3 +h) – расстояние между центрами Земли и спутника.
После преобразований получим:
Подкоренное выражение удобно умножить и разделить на квадрат радиуса Земли, так как
Для периода обращения имеем:
Ответ: период обращения спутника 1 ч 42 мин, а скорость 7,4 км/с.
