Метод наименьших квадратов

Пусть в результате получена таблица значений функции 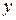для ряда значений независимой переменной :

				…
				…

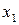
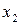
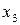
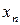
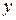
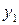
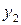
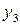
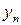
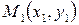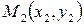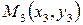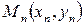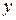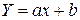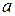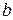Если точки , , , …, примерно располагаются на одной прямой, это означает, что зависимость между и близка к линейной: . Подберем неизвестные коэффициенты и так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.

Широко распространенным методом решения данной задачи является метод наименьших квадратов. Этот метод заключается в следующем.

Рассмотрим сумму квадратов разностей значений 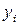, даваемых экспериментом, и функции в соответствующих точках, т. е.

.

Подбираем параметры 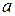и 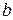так, чтобы эта сумма имела наименьшее значение. Поскольку 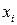и 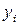– постоянные, то указанная сумма есть функция параметров 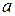и :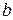

.

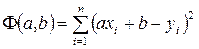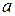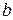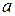Чтобы найти значения параметров и , воспользуемся необходимыми условиями экстремума функции двух переменных: найдем частные производные от по переменным и 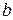и приравниваем их к нулю:

,

.

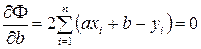Параметры 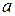и 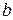найдем из этой системы. Для этого перепишем ее в следующем виде:

Для определения чисел 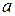и 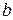получили систему двух уравнений перовой степени. Можно доказать, что эта система всегда имеет единственное решение и что для найденных чисел 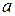и 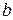функция достигает минимума. Подставляя найденные значения 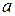и 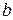в уравнение 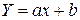, получим линейную функцию, наилучшим образом отражающую зависимость между величинам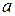и и 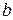, полученными из опыта.

Пример. Полученные из опыта значения функции при различных значениях независимой переменной приведены в таблице:

			1,5	2,1
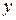
	2,9	6,3	7,9		13,2

Методом наименьших квадратов найти функцию 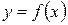в виде .

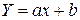Решение. Для решения этой задачи составим таблицу.

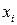
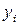
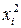
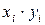
		2,9
	1,0	6,3		6,3
	1,5	7,9	2,25	11,85
	2,1	10,0	4,41
	3,0	13,2	9,0	39,6
∑	7,6	40,3	16,66	78,75

Воспользуемся для нахождения параметров 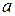и 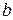системой в которой ; ; ; ;

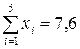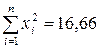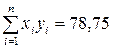получим .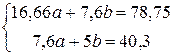

Решим систему. Для этого выразим 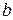из второго уравнения:

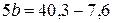
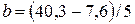
Подставим в первое уравнение:

.

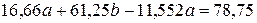
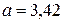Отсюда .

Итак, 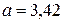, , 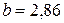и, следовательно, искомая функция имеет вид:

.

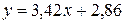Правильность вычислений легко проверить, сделав чертеж.

На координатной плоскости строим точки по результатам таблицы и график

полученной прямой. В случае верного решения точки будут расположены близко к прямой.