Напряженное состояние в каждой точке сплошной среды характеризуется всей совокупностью напряжений, действующих в данной точке, т.е. множеством векторов напряжений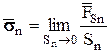 
для всех плоских сечений, проведенных через точку. В выражении для напряжения 
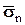индекс n указывает направление сечения, определяемое нормалью 
, 
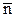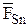- равнодействующая сил, действующих на произвольную односвязную площадку 
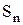(секущую площадку) в этом сечении, включающую рассматриваемую точку (рис. 1), а 
означает, что предел рассматривается при «стягивании» этой площадки в рассматриваемую точку. Напряжения называют также поверхностной плотностью сил. В общем случае направления напряжений не совпадают с нормалями.
Рисунок 1
Другим способом определения напряженного состояния в точке является выделение около нее произвольного односвязного выпуклого объема среды и рассмотрения сил, действующих на каждый участок поверхности выделенного объема, т.е. - поверхностных сил (рис.2). Пусть для рассматриваемой среды эти поверхностные силы в каждой точке целиком определяются направлением касательной плоскости к этой поверхности, т.е. - не зависят, например, от кривизны поверхности. Тогда при «стягивании» объема в точку и выполнении указанного выше предельного перехода от поверхностных сил к напряжениям для каждого участка поверхности (также стягиваемого в точку), множество получаемых векторов напряжений также будет характеризовать напряженное состояние.
Следует обратить внимание, что напряженное состояние для точки, находящейся внутри среды, целиком определяется так называемыми внутренними силами, хотя зависит от всей системы взаимодействий рассматриваемой среды, проявляющейся через эти внутренние силы.
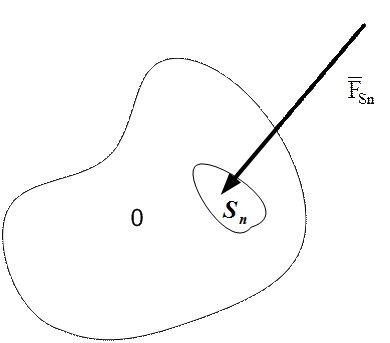
Рисунок 2
Для внутренних сил в сплошной среде справедливо все то, что присуще им в любой механической системе, в частности - независимость от системы отсчета и противоположность для двух сторон любой секущей площадки. Очевидно, что это же справедливо и для напряжений.
Если взаимодействие между частицами среды носит только контактный характер (отсутствует так называемое «дальнодействие»), то напряженное состояние в точке можно полностью определить по трем напряжениям, действующим в трех взаимно перпендикулярных направлениях.
Чтобы убедится в этом, достаточно рассмотреть условия равновесия произвольного элементарного объема в виде прямоугольного тетраэдра (рис.3).
Так как объем выбран произвольно, то без потери общности систему координат можно выбрать так, чтобы вершина тетраэдра, в которой грани сходятся под прямыми углами, находилась в начале координат (точка О на рис.3), а три ребра, сходящиеся в этой вершине - вдоль осей этой системы. Нормали трех граней параллельны соответствующим осям системы координат, а углы между нормалью 
четвертой грани и координатными осями обозначены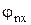 
, 
, 
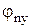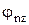. Здесь 
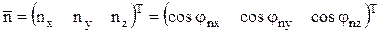- орт нормали четвертой грани, h – расстояние от вершины в начале координат до грани Sn (высота тетраэдра).
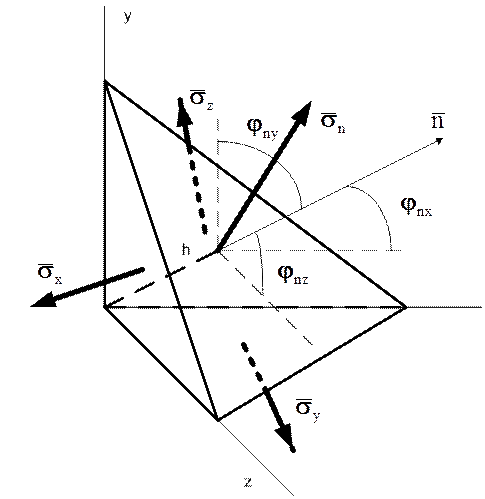
Рисунок 3
Рассмотрение условий равновесия не ограничивает общности рассмотрения, если в эти условия включить так называемые силы инерции, возникающие при движении выделенного объема с ускорением.
На рассматриваемый объем действуют поверхностные силы на его гранях и массовые (объемные) силы по его объему.
Поверхностные внутренние силы на гранях тетраэдра определяются выражениями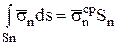 
, 
, 
, 
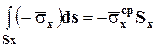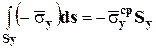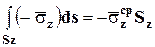, где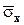 
, 
, 
, 
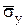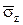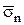- напряжения в точках площадок с нормалями, направленными вдоль осей x, y и z (в положительном направлении этих осей), и площадки с нормалью 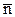соответственно, 
, 
, 
, 
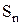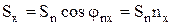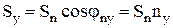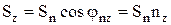- площади граней тетраэдра, а 
, 
, 
, 
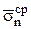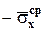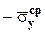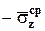- средние напряжения на гранях тетраэдра. Знаки минус объясняются тем, что внешние нормали гране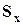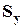й 
, 
и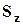 
направлены в отрицательном направлении соответствующих координатных осей.
Массовые силы (к которым относятся и инерционные) принято описывать интенсивностью, или объемной плотностью сил, которая для каждой точки определяется выражением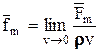 
, где v - элементарный объем вокруг точки, 
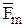- действующая на этот объем суммарная массовая сила, r - плотность среды в этой точке. Поэтому суммарную массовую силу, действующую на рассматриваемый тетраэдр, можно представить в виде 
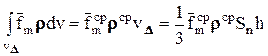, где 
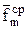и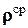 
- средние значения интенсивности массовых сил и плотности в объеме тетраэдра, 
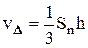- объем тетраэдра.
В этих обозначениях условия равновесия для сил примут вид
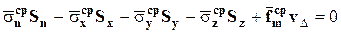, или
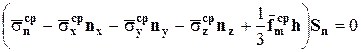, откуда
.
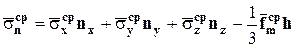При «стягивании» объема в начало координат с сохранением ориентации всех граней, т.е. при h®0, средние напряжения становятся равными напряжениям в точке О по соответствующим направлениям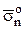 
, 
, 
, 
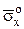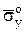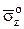, а слагаемое 
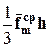обращается в ноль (массовые силы оказываются бесконечно малыми величинами более высокого порядка по сравнению с поверхностными силами). Следовательно,
.
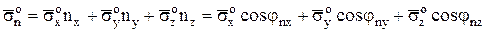Так как точка О и направление площадки выбраны произвольно, то данный вывод пригоден для напряжения в любом направлении любой точки, т.е.
.
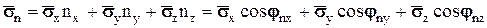Полученное выражение можно записать в скалярном виде, выразив проекции напряжения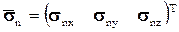 
через проекции напряжений 
, , 
;
;
,
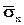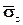
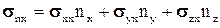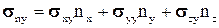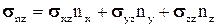или в векторно-матричном виде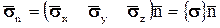 
,
где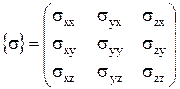 
, а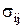 
- проекция на ось j напряжения на площадке, нормальной оси i, для 
.
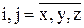Таким образом, для определения напряжения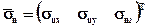 
в любом направлении 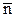достаточно знать напряжения , 
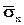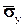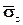, в трех взаимно перпендикулярных направлениях, или матрицу 
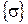, которая называется тензором напряжений.
Очевидно, что диагональные элементы тензора напряжений представляют собой нормальные, а внедиагональные - касательные напряжения на соответствующих площадках. Принято нормальные напряжения обозначать литерой p, т.е.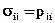 
для 
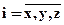, и называть напряжениями растяжения - сжатия, или давления, а касательные – литерой t, т.е. 
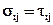при 
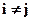для 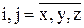, и называть их напряжениями сдвига, или трения. Аналогичные названия – силы давления и силы трения, используются и для соответствующих проекций внутренних сил.
В этих обозначениях тензор напряжений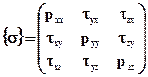 
.
Если внедиагональные элементы матрицы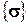 
равны нулю, то 
; 
; 
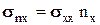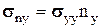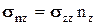. Так как при отсутствии касательных напряжений полное напряжение является нормальным, то 
; 
; 
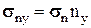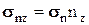. Следовательно 
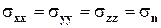. Другими словами, при отсутствии касательных напряжений вектора напряжения в любом направлении являются нормальными и одинаковыми по величине, т.е. напряженное состояние описывается множеством одинаковых по величине векторов нормальных напряжений. Используя введенные обозначения для нормальных напряжений последнее соотношение можно записать также в виде 
.
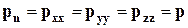Касательные напряжения будут отсутствовать, если частицы жидкости не перемещаются относительно друг друга, т.е. – в статическом состоянии. Поэтому полученный результат является формальной записью известного закона Паскаля для гидростатики, а величина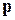 
называется гидростатическим давлением.
Касательные напряжения будут отсутствовать также и в идеальной жидкости даже при относительном движении ее частиц из-за отсутствия трения между ними. Для таких жидкостей также удобно использовать понятие давления, которое совпадает с гидростатическим.
В общем случае движения реальной жидкости касательные напряжения не нулевые, а нормальные – различные в различных направлениях. Если взаимодействие между частицами среды носит только контактный характер, то матрица 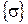является симметричной, т.е.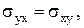 
.
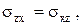
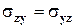Эта симметрия следует из того, что равновесие любого элементарного объема (с учетом инерционных сил) обеспечивается не только рассмотренным выше равенством сил, но и равенством моментов.
Для доказательства симметричности удобно рассмотреть элементарный объем в виде прямоугольного параллелепипеда с одной из вершин в начале координат и ребрами dx, dy, dz, ориентированными параллельно осям системы координат (рис. 4).
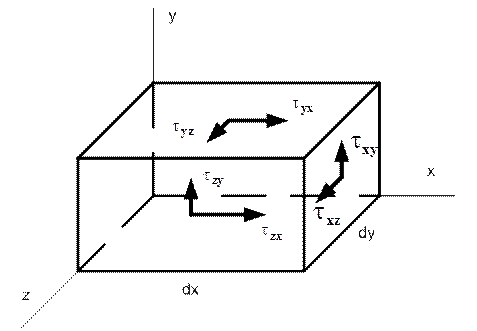
Рисунок 4
Из всех действующих на этот объем сил момент относительно оси х создают лишь проекци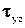и 
и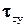 
напряжени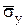й и 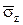на соответствующих площадках. Так как площади этих площадок равны dxdz и dxdy, то проекции сил равны 
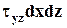и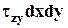 
. Плечи этих сил относительно оси х равны dy и dz, следовательно, создаваемые ими моменты равны 
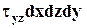и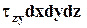 
, а условие равновесия 
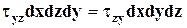, откуда следует, что 
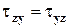, или .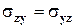
Рассмотрев моменты относительно осей y и z, аналогичным образом можно получить остальные равенства касательных напряжений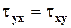 
, или 
и 
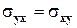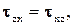или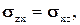 
т.е. равенств, показывающих симметричность матрицы .
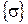В общем случае величину нормального напряжения pn (напряжения давления) в произвольном направлении, очевидно, можно найти из соотношения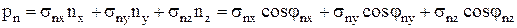 
, или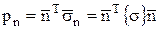 
, а учитывая выражения для проекций вектора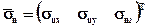
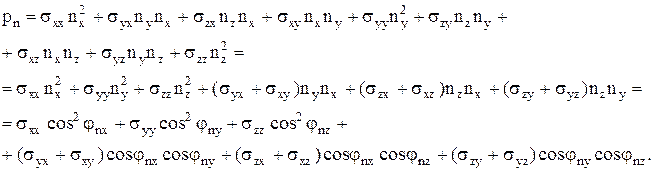
Отсюда видно (всем тем, кто знает линейную алгебру или аналитическую геометрию), что при симметричности матрицы 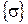, т.е. при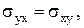 
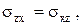
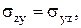концы всех векторов 
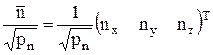, исходящих из рассматриваемой точки, образуют эллипсоид с центром в этой точке. Известно также, что полуоси этого эллипсоида имеют длину 
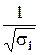, где 
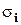- собственные значения матрицы .
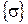Выражение для pn, являющееся квадратичной формой, может быть преобразовано в сумму квадратов
,
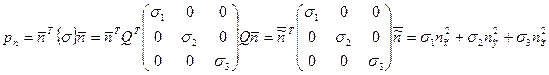где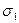 
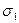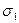, , - собственные числа матрицы 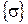. Это преобразование соответствует повороту системы координат от 
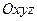к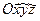 
с помощью матрицы поворота 
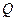, называемой матрицей перехода или матрицей направляющих косинусов. Вектор 
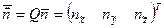представляет собой единичную нормаль в повернутой системе координат 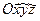. Для существования такого преобразования достаточно, чтобы все собственные значения матрицы 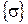были действительными, что выполняется, так как эта матрицы является симметричной.
Матрица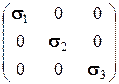 
, очевидно, является тензором напряжений, построенным для системы координат 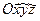. Для направлений, совпадающих с осям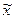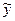и 
, 
и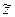 
, соотношение для нормальных напряжений, очевидно, приводит к равенствам 
, 
, 
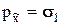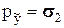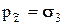, что и следовало ожидать, так как диагональность тензора напряжений как раз и означает отсутствие касательных напряжений, т.е. - совпадение полных напряжений по осям с нормальными. Эти напряжения называют главными напряжениями, ос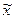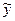и , и 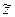- главными осями, а элементарные площадки, нормальные к ним – главными площадками напряженного состояния в рассматриваемой точке. Смысл этих названий становится очевидным, если через главные напряжения записать проекции напряжения в произвольном направлении
; 
; 
,
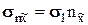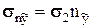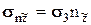выразить отсюда направляющие косинусы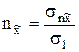 
; 
; 
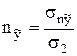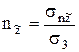, и учесть, что сумма квадратов направляющих косинусов равна 1, т.е. 
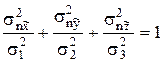. Последнее уравнение является каноническим уравнением эллипсоида с центром в рассматриваемой точке с главными осями вдоль координатных осей и длиной полуосей 
, 
, 
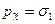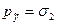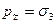. Этот эллипсоид является геометрическим местом концов всех векторов напряжений 
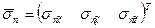для рассматриваемой точки и называется эллипсоидом напряжений.
Представление напряженного состояния в виде эллипсоида напряжений дает не только наглядный геометрический образ, но и позволяет ввести понятие давления, пригодного для общего случая движения сплошной среды.
Давлением, или гидродинамическим давлением 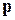называют среднее значение главных напряжений эллипсоида напряжений, т.е.
.
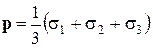Следует заметить, что во всех случаях, когда касательные напряжения отсутствуют, эллипсоид напряжений становится сферой, а величина давления совпадает с радиусом этой сферы.
