‘азой называетс€ термодинамически равновесное состо€ние вещества, отличаютс€ не химическим составом, а физическим свойствами от других равновесных состо€ний того же вещества (например, вода может находитьс€ в трех фазах: жидком, твердом и в виде пара). ѕереход вещества из одной фазы в другую называетс€ фазовым переходом.
–азличают фазовые переходы I и II рода. ‘азовый переход I рода св€зан с поглощением или выделением тепла (например, плавление и кристаллизаци€). ‘азовый переход II рода не св€заны с теплотой (например, переход некоторых веществ при определенных температурах в сверхпровод€щее состо€ние.
ƒл€ характеристики фазовых переходов используютс€ диаграммы состо€ний (обычно в координатах – Ц “). Ќа этих диаграммах можно найти точку одновременного равновесного осуществлени€ трех фаз Ц тройную точку. Ќапример, тройна€ точка дл€ воды 273,12 . “ермодинамика позвол€ет рассчитать равновесие двух фаз одного вещества, пользу€сь уравнением лапейрона Ц лаузиуса:
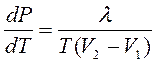 ,
,
где производна€ от равновесного давлени€ по температуре зависит от теплоты фазового перехода λ, температуры перехода и изменени€ объема фаз (например, при замерзании воды ее объем возрастает).
2.12. –еальные газы. ”равнение ¬ан Ц дер Ц ¬аальса
”равнение ћенделеева Ц лапейрона дл€ одного мол€ идеального газа имеет вид: PV= RT. ћолекулы реального газа имеют размеры ~10-10 м и поэтому следует учитывать их собственный объем, т.е. в уравнение ћенделеева Ц лапейрона вводитс€ поправка Ђ bї на объем, занимаемый самими молекулами (V 0 Ц b).
ƒействие сил взаимодействи€ между молекулами реального газа приводит к дополнительному внутреннему давлению Pi = a / V 02, где V 0 Ц объем 1 мол€ газа, т.е.
(– + Pi) = (– + a/V02)
ѕоправка Ђаї и Ђbї посто€нны дл€ данного газа. — учетом этого дл€ 1 мол€ реального газа уравнение состо€ни€ Ц уравнение ¬ан Ц дер Ц ¬аальса примет вид
(– + a/V02) (V0 - b) = RT (2.54)
Ёто уравнение из-за сделанных упрощений приближенно описывает состо€ние реального газа.
Ќа рис. 2.13 проведены изотермы ¬ан Ц дер Ц ¬аальса дл€ пропана при различных температурах. ≈сли сравнивать их с изотермой идеального газа (рис.2.7), то заметим, что только при высоких температурах они схожи.

–ис.2.13
ѕри низких температурах изотермы отличаютс€ горбами, при этом одному давлению соответствует три объема. —реди изотерм ¬ан-дер-¬аальса есть така€, котора€ разграничивает изотермы с УгорбамиФ от изотерм без УгорбовФ (“=388,201 на –ис.2.13). ќна отдел€ет области двухфазного состо€ни€ вещества (газообразного и жидкого) и однофазного (газообразного). Ёта изотерма называетс€ критической и соответствующие ей параметры –, V и “ также называютс€ критическими. ѕон€тие критической температуры “ к было введено ћенделеевым. ћенделеев рассматривал ее как температуру, при которой исчезают силы взаимодействи€ между молекулами и жидкость превращаетс€ в пар независимо от давлени€ и занимаемого объема (на изотерме ей соответствует критическа€ точка).






