Лекция 2. Сходящиеся последовательности. Монотонные последовательности. Основные теоремы.
Свойства сходящихся последовательностей
Теорема 1
Сходящаяся последовательность имеет только один предел.
Доказательство
Пусть a и b – пределы сходящейся последовательности  . Используя формулу (2) можно записать
. Используя формулу (2) можно записать  и
и  , где
, где  ,
,  - бесконечно малые последовательности. Вычитая, получим
- бесконечно малые последовательности. Вычитая, получим  Так как, все элементы последовательности имеют одно и тоже значение b-a, то по теореме 5 (см. ранее) b-a=0 и b=a. Теорема доказана.
Так как, все элементы последовательности имеют одно и тоже значение b-a, то по теореме 5 (см. ранее) b-a=0 и b=a. Теорема доказана.
Теорема 2
Сходящаяся последовательность ограничена.
Доказательство
Пусть последовательность  сходящаяся и а – ее предел. Имеет место формула
сходящаяся и а – ее предел. Имеет место формула  ,
,  - бесконечно малая последовательность. Так как бесконечно малая последовательность
- бесконечно малая последовательность. Так как бесконечно малая последовательность 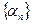 - ограничена (теорема 3), то
- ограничена (теорема 3), то  справедливо
справедливо  . Поэтому
. Поэтому  для всех номеров n, что и означает ограниченность последовательности
для всех номеров n, что и означает ограниченность последовательности  .
.
Замечание
Ограниченная последовательность может быть и не сходящейся.
Например
1,-1,1,-1,… - ограничена, но не сходящаяся. Если бы последовательность сходилась, то 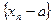 и
и  - бесконечно малые последовательности и
- бесконечно малые последовательности и  была бы бесконечно малой последовательностью, но
была бы бесконечно малой последовательностью, но 
Теорема 3
Сумма сходящихся последовательностей  и
и  есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей
есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей  и
и  .
.
Доказательство
Пусть  и
и 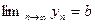 . Тогда
. Тогда  и
и  , соответственно
, соответственно  . Таким образом, последовательность
. Таким образом, последовательность  - бесконечно малая, и поэтому последовательность
- бесконечно малая, и поэтому последовательность  сходится и имеет своим пределом a+b.
сходится и имеет своим пределом a+b.
Теорема 4
Разность сходящихся последовательностей  и
и  есть сходящаяся последовательность, предел которой равен разности пределов последовательностей
есть сходящаяся последовательность, предел которой равен разности пределов последовательностей  и
и  . Доказательство аналогичное.
. Доказательство аналогичное.
Теорема 5
Произведение сходящихся последовательностей  и
и  есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей
есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей  и
и  .
.
Доказательство
Пусть  и
и  . Тогда
. Тогда  и
и  , соответственно
, соответственно
 . Но в силу теоремы 4 (для бесконечно малых последовательностей, следствия из него и теоремы 1)
. Но в силу теоремы 4 (для бесконечно малых последовательностей, следствия из него и теоремы 1)  - бесконечно малая последовательность. То есть
- бесконечно малая последовательность. То есть  сходится и ее предел - ab.
сходится и ее предел - ab.
Лемма
Если последовательность  сходится, то есть
сходится, то есть  , то, начиная с некоторого номера, определена последовательность
, то, начиная с некоторого номера, определена последовательность  , которая является ограниченной.
, которая является ограниченной.
Доказательство
Пусть  . Так как
. Так как  . Пусть N – номер, соответствующий этому
. Пусть N – номер, соответствующий этому 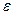 , начиная с которого выполняется неравенство
, начиная с которого выполняется неравенство  . Из этого неравенства следует, что при
. Из этого неравенства следует, что при 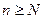 выполняется неравенство
выполняется неравенство  . Действительно
. Действительно 
Поэтому, при 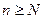 имеем
имеем  . Следовательно, начиная с этого номера N, можно рассматривать последовательность
. Следовательно, начиная с этого номера N, можно рассматривать последовательность  , и эта последовательность ограничена. Лемма доказана.
, и эта последовательность ограничена. Лемма доказана.
Теорема 6
Частное двух сходящихся последовательностей  и
и  при условии, что предел последовательности
при условии, что предел последовательности  отличен от 0, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей
отличен от 0, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей  и
и  .
.
Доказательство
Из леммы следует, что, начиная с некоторого номера N элементы  не равны 0 и последовательность
не равны 0 и последовательность  - ограничена. Начиная с этого номера, рассмотрим последовательность
- ограничена. Начиная с этого номера, рассмотрим последовательность 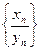 . Пусть
. Пусть  и
и  .
.
Докажем, что  - бесконечно малая последовательность. Так как
- бесконечно малая последовательность. Так как  и
и  ,
,
то  . Так как
. Так как  - ограничена, а последовательность
- ограничена, а последовательность  - бесконечно малая, то последовательность
- бесконечно малая, то последовательность  - бесконечно малая, то есть
- бесконечно малая, то есть 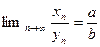 . Теорема доказана.
. Теорема доказана.






