Вот и еще одна средняя, которая связана с погрешностями.
Средняя квадратическая погрешность (СКП) является мерой точности результатов измерений либо функций измеренных величин и является вероятностной характеристикой.
Рис. 3.1. Нормальный закон распределения
случайных погрешностей.
Предположим, что нам известно значение средней квадратической погрешности m. В соответствии с нормальным законом распределения график распределения истинных погрешностей по виду будет подобен графику рис. 3.1. Параметр r характеризует частоту (или частость) появления случайных погрешностей той или иной величины и знака. При этом вероятность появления погрешностей в заданном наперёд диапазоне, например, ± m, определяется площадью фигуры, ограниченной кривой распределения и отрезками ординат на значениях + m и - m. Для нормального закона распределения вероятность появления погрешностей в установленных диапазонах равна следующим значениям:
- для диапазона ± m ® Р = 68,3% (» 68%);
- для диапазона ±2 m ® Р = 95,5% (» 95%);
- для диапазона ±3 m ® Р = 99,7% (практически 100%).
Таким образом, только в 3-х случаях из 1000 может появиться погрешность, превышающая значение 3 m. Погрешности, по абсолютной величине превышающие 3 m (предельную погрешность), принято считать грубыми, и результаты измерений, содержащие эту грубую погрешность, исключают из дальнейшей обработки. В некоторых случаях, для ужесточения требований к точности измерений, устанавливают предельную погрешность в диапазоне от 2 m до 3 m.
Таблица 3.1
Значения коэффициента Стьюдента (t) для различных вероятностей (Р)
| t | P % | t | P % | t | P % |
| 0,1 | 8,0 | 1,1 | 72,9 | 2,1 | 96,4 |
| 0,2 | 15,9 | 1,2 | 77,0 | 2,2 | 97,2 |
| 0,3 | 23,6 | 1,3 | 80,6 | 2,3 | 97,9 |
| 0,4 | 31,1 | 1,4 | 83,8 | 2,4 | 98,4 |
| 0,5 | 38,3 | 1,5 | 86,6 | 2,5 | 98,8 |
| 0,6 | 45,1 | 1,6 | 89,0 | 2,6 | 99,1 |
| 0,7 | 51,6 | 1,7 | 91,1 | 2,7 | 99,3 |
| 0,8 | 57,6 | 1,8 | 92,8 | 2,8 | 99,5 |
| 0,9 | 63,2 | 1,9 | 94,3 | 2,9 | 99,6 |
| 1,0 | 68,3 | 2,0 | 95,5 | 3,0 | 99,7 |
Часто значение СКП указывают с коэффициентом t (коэффициент Стьюдента), который и определяет доверительный вероятностный интервал (х ± tm) результата измерений при установленном уровне вероятности Р. Для этого удобно пользоваться табл. 3.1.
Например, необходимо определить доверительный интервал для величины Х с вероятностью 90%. По таблице интерполированием находим, что для Р1 = 89,0% t1 = 1,6, для Р2 = 91,1% t2 = 1,7: tх = 1,6476» 1,65.
Это значит, что результат измерений с вероятностью 90% находится в пределах (Х ± 1,65 m).
Если измеряемая величина Х известна, то значение СКП определяется по формуле Гаусса:
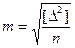, (3.9)
где Δ - истинные погрешности измерений.
Напомним, что знак [...] – это знак гауссовой суммы.
Для случаев, когда измеряемая величина неизвестна, используется формула Бесселя:
, (3.10)
где v - уклонения результатов измерений от среднего арифметического.
Как видно из формул (3.9) и (3.10), в случае, когда измеряемая величина известна, для оценки точности достаточно уже одного измерения (оно и является необходимым). Как уже указывалось выше, чаще всего формулу Гаусса используют при оценках точности эталонируемых приборов при измерении известных величин (эталонов). Для оценки точности по формуле Бесселя необходимыми являются как минимум два измерения. Формула Бесселя используется при оценках точности результатов массовых (многократных) измерений одной величины, заранее неизвестной.
При возрастании числа измерений значения СКП, полученные по формулам Гаусса и Бесселя, становятся практически одинаковыми (примерно с n ³ 20). При этом значение СКП одного измерения стремится к пределу mпред, который определяется точностью прибора, точностью метода или программы измерений. Очевидно, выше об этом уже было сказано, что на практике невозможно, да и нецелесообразно по ряду причин, обеспечивать весьма большое число измерений одной величины. При этом практическое число измерений должно обеспечивать получение результата измерения с заданной точностью при установленном уровне доверительной вероятности.
Поскольку число измерений является ограниченным, то сама СКП содержит погрешность, определяемую по приближенной формуле:
. (3.11)
Она так и называется – средняя квадратическая погрешность средней квадратической погрешности (СКП СКП).
Здесь уместно возвратиться к классификации погрешностей. Не все виды погрешностей рассмотрены нами выше.
Часто при исследованиях рядов погрешностей измерений используют т.н. вероятную погрешность, которую обозначают буквой r. Величина вероятной погрешности может быть оценена по приближенной формуле
(3.12)
в предположении, конечно, что распределение погрешностей подчиняется нормальному закону.
Вероятную погрешность называют еще срединной погрешностью. Если не хочется делать вычисления по формуле (3.12), потому что в неё входит значение m, которое необходимо получить по формуле Бесселя, то можно определить вероятную или срединную погрешность, расположив ряд погрешностей по их возрастанию по абсолютным величинам. В середине полученного ряда и будет находиться значение этой погрешности. Это если число погрешностей нечётное. А если оно чётное, то срединной погрешностью будет среднее значение соседних погрешностей в середине ряда.
Не надо путать срединную погрешность со средней погрешностью vo, которую можно получить тоже по простой формуле:
. (3.13)
Здесь также требуется условие подчинения ряда измерений (погрешностей) нормальному закону.
Средняя погрешность является математическим ожиданием абсолютных значений отклонений результатов измерений какой-либо величины от математического ожидания для этих результатов. Приближенно значение средней погрешности можно оценить по формуле:
, (3.14)
где vi – уклонения результатов измерений от их среднего арифметического.
Часто формулу (3.13) используют для предварительной оценки средней квадратической погрешности:
. (3.15)
