 9.1 ‘раунгоферовы линии -- это линии поглощени€ в видимой части спектра —олнца (линий в других област€х спектра ‘раунгофера в начале 19 в. наблюдать, естественно, не мог). Ќар€ду с другими причинами, уширение этих линий вызываетс€ тепловым движением атомов в атмосфере —олнца. ќценим характерную тепловую скорость атомов водорода на —олнце. »з услови€
9.1 ‘раунгоферовы линии -- это линии поглощени€ в видимой части спектра —олнца (линий в других област€х спектра ‘раунгофера в начале 19 в. наблюдать, естественно, не мог). Ќар€ду с другими причинами, уширение этих линий вызываетс€ тепловым движением атомов в атмосфере —олнца. ќценим характерную тепловую скорость атомов водорода на —олнце. »з услови€

находим

ѕодставл€€ значени€ 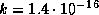 эрг/K (посто€нна€ Ѕольцмана), T =5800 K (температура "поверхности" —олнца) и
эрг/K (посто€нна€ Ѕольцмана), T =5800 K (температура "поверхности" —олнца) и  г (масса атома водорода мало отличаетс€ от массы протона), получаем
г (масса атома водорода мало отличаетс€ от массы протона), получаем 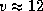 км/с. (Ёто число полезно помнить. ќно пор€дка скорости звука в атмосфере —олнца.) ѕо формуле эффекта ƒоплера при такой лучевой скорости длина волны видимого света
км/с. (Ёто число полезно помнить. ќно пор€дка скорости звука в атмосфере —олнца.) ѕо формуле эффекта ƒоплера при такой лучевой скорости длина волны видимого света 
 ) смещаетс€ на величину
) смещаетс€ на величину 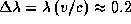
 . —оответствующа€ ширина линий пор€дка
. —оответствующа€ ширина линий пор€дка 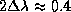
 , так как скорости частиц газа могут быть направлены как к наблюдателю, так и в противоположном направлении.
, так как скорости частиц газа могут быть направлены как к наблюдателю, так и в противоположном направлении.
Ёта оценка относитс€ к водороду. ƒл€ атома с массой m ширина линии будет в 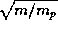 раз меньше (почему?).
раз меньше (почему?).
Ќайденные нами ширины -- минимальные: тепловые скорости есть всегда. ¬ действительности существуют и другие причины уширени€. ¬ итоге сильные линии (в частности, и бальмеровские линии водорода) оказываютс€ значительно шире.
 9.2 »з-за вращени€ один край диска приближаетс€ к нам, другой удал€етс€. ѕоэтому лини€, котора€ была бы бесконечно узкой у невращающейс€ звезды, оказываетс€ уширенной -- ведь к нам приходит излучение со всего диска, а из-за вращени€ в разных его точках лучева€ скорость, а значит, и вызванное ею доплеровское смещение различны. ≈сли ось вращени€ перпендикул€рна к лучу зрени€, то доплеровское уширение линии, обусловленное вращением, будет составл€ть
9.2 »з-за вращени€ один край диска приближаетс€ к нам, другой удал€етс€. ѕоэтому лини€, котора€ была бы бесконечно узкой у невращающейс€ звезды, оказываетс€ уширенной -- ведь к нам приходит излучение со всего диска, а из-за вращени€ в разных его точках лучева€ скорость, а значит, и вызванное ею доплеровское смещение различны. ≈сли ось вращени€ перпендикул€рна к лучу зрени€, то доплеровское уширение линии, обусловленное вращением, будет составл€ть

(ј что будет, если угол наклона оси вращени€ к лучу зрени€ не  , а i?)
, а i?)
ќбратимс€ к конкретному случаю, указанному в условии задачи. –адиус звезды спектрального класса B0V можно прин€ть равным 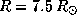 . ѕоэтому периоду осевого вращени€
. ѕоэтому периоду осевого вращени€ 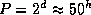 соответствует скорость вращени€ на экваторе
соответствует скорость вращени€ на экваторе 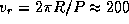 км/с. Ћини€ с длиной волны
км/с. Ћини€ с длиной волны 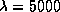
 будет иметь
будет иметь 
 .
.
 9.3 Ћинии H и K Ca II -- резонансные, т.е. они возникают при переходах с основного уровн€. Ћинии же
9.3 Ћинии H и K Ca II -- резонансные, т.е. они возникают при переходах с основного уровн€. Ћинии же  и
и 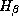 возникают при переходах с первого возбужденного уровн€, отсто€щего от основного на 10.2 э¬. ѕри температуре
возникают при переходах с первого возбужденного уровн€, отсто€щего от основного на 10.2 э¬. ѕри температуре  K на этом уровне находитс€ лишь очень мала€ дол€ атомов водорода, подавл€ющее же большинство -- на основном уровне. Ќаселенность i -го уровн€
K на этом уровне находитс€ лишь очень мала€ дол€ атомов водорода, подавл€ющее же большинство -- на основном уровне. Ќаселенность i -го уровн€ 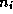 можно оценить по формуле Ѕольцмана
можно оценить по формуле Ѕольцмана

где 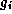 -- статистический вес i -го уровн€ (дл€ водорода
-- статистический вес i -го уровн€ (дл€ водорода 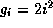 ) и
) и  -- энерги€ его возбуждени€ (10.2 э¬ дл€ i = 2, т.е. дл€ первого возбужденного уровн€ водорода). ѕоскольку энергии в 1 э¬ соответствует температура 11600 , то при
-- энерги€ его возбуждени€ (10.2 э¬ дл€ i = 2, т.е. дл€ первого возбужденного уровн€ водорода). ѕоскольку энергии в 1 э¬ соответствует температура 11600 , то при 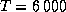 оказываетс€, что
оказываетс€, что 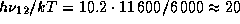 . ѕоэтому при
. ѕоэтому при 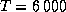 K дол€ атомов водорода, наход€щихс€ на втором уровне, составл€ет всего
K дол€ атомов водорода, наход€щихс€ на втором уровне, составл€ет всего  . Ќо
. Ќо 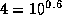 (напоминаем, что
(напоминаем, что  ), а
), а 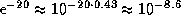 , так что дол€ атомов на втором уровне составл€ет
, так что дол€ атомов на втором уровне составл€ет 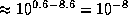 . »х концентраци€ существенно ниже концентрации ионов кальци€ (содержание кальци€
. »х концентраци€ существенно ниже концентрации ионов кальци€ (содержание кальци€  от водорода; кальций в солнечной атмосфере сильно ионизован, так как энерги€ его ионизации сравнительно невелика,
от водорода; кальций в солнечной атмосфере сильно ионизован, так как энерги€ его ионизации сравнительно невелика,  э¬). ¬ итоге резонансные линии иона кальци€ оказываютс€ сильнее бальмеровских линий.
э¬). ¬ итоге резонансные линии иона кальци€ оказываютс€ сильнее бальмеровских линий.
|
|
|
 9.4 „тобы ответить на поставленные вопросы, следует прежде всего пон€ть, почему есть бальмеровский скачок. ѕоглощение излучени€ в атмосферах с температурой
9.4 „тобы ответить на поставленные вопросы, следует прежде всего пон€ть, почему есть бальмеровский скачок. ѕоглощение излучени€ в атмосферах с температурой  K вызываетс€ нейтральным водородом. ѕо коротковолновую сторону от бальмеровского предела при
K вызываетс€ нейтральным водородом. ѕо коротковолновую сторону от бальмеровского предела при 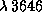
 \ (скажем, на
\ (скажем, на 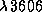
 ) излучение способно ионизовать атомы водорода со всех уровней, начина€ со второго, по длинноволновую сторону от этого предела (скажем, на
) излучение способно ионизовать атомы водорода со всех уровней, начина€ со второго, по длинноволновую сторону от этого предела (скажем, на 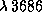
 ) фотоны могут ионизовать водород лишь с третьего и более высоких уровней. ¬ результате на
) фотоны могут ионизовать водород лишь с третьего и более высоких уровней. ¬ результате на 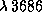
 \ атмосфера оказываетс€ более прозрачной, и мы видим более глубокие и потому более гор€чие ее слои. »злучение их сильное. ѕо коротковолновую сторону от предела (на
\ атмосфера оказываетс€ более прозрачной, и мы видим более глубокие и потому более гор€чие ее слои. »злучение их сильное. ѕо коротковолновую сторону от предела (на 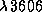
 ) непрозрачность газа велика, излучение приходит лишь из самых поверхностных, а значит, более холодных слоев, и потому оно слабее.
) непрозрачность газа велика, излучение приходит лишь из самых поверхностных, а значит, более холодных слоев, и потому оно слабее.
“еперь уже легко ответить и на вопрос о потемнении. “ам, где непрозрачность велика (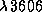
 ), во всех точках диска излучение приходит почти из одних и тех же, самых поверхностных слоев. ѕоэтому потемнение к краю должно быть мало. — излучением по длинноволновую сторону от предела (
), во всех точках диска излучение приходит почти из одних и тех же, самых поверхностных слоев. ѕоэтому потемнение к краю должно быть мало. — излучением по длинноволновую сторону от предела (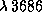
 ) положение другое. ¬ центре диска оно приходит со сравнительно большой глубины, где гор€чо, а на краю луч зрени€ скользит по атмосферным сло€м, и излучение приходит только из самых наружных холодных слоев. «начит, на этих длинах волн должно быть значительное потемнение.
) положение другое. ¬ центре диска оно приходит со сравнительно большой глубины, где гор€чо, а на краю луч зрени€ скользит по атмосферным сло€м, и излучение приходит только из самых наружных холодных слоев. «начит, на этих длинах волн должно быть значительное потемнение.
ћожно утверждать, что отношение €ркостей в центре и на краю по длинноволновую сторону от предела заведомо больше, чем величина наблюдаемого в спектре звезды скачка (поймите, почему).
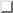 9.5 ћы настолько привыкли к тому, что излучение —олнца в первом приближении можно считать чернотельным, что обычно не задаемс€ вопросом, почему, собственно, это так. ћежду тем вопрос нетривиален. ƒействительно, если бы температура —олнца была не 6000 K, а 10000 K, то оно было бы звездой класса A0V, и спектр был бы совсем не похож на планковский -- имелс€ бы большой бальмеровский скачок на
9.5 ћы настолько привыкли к тому, что излучение —олнца в первом приближении можно считать чернотельным, что обычно не задаемс€ вопросом, почему, собственно, это так. ћежду тем вопрос нетривиален. ƒействительно, если бы температура —олнца была не 6000 K, а 10000 K, то оно было бы звездой класса A0V, и спектр был бы совсем не похож на планковский -- имелс€ бы большой бальмеровский скачок на 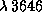
 и т. д. “ак почему же распределение энергии в спектре —олнца похоже на планковское? ѕо сути дела, причина этого в том, что атмосфера —олнца почти сера€, т.е. ослабл€ет проход€щее через нее излучение неселективно. Ёто вызвано тем, что основным источником непрозрачности газа в солнечной атмосфере €вл€етс€ не нейтральный водород, как у звезд класса A (последний поглощает излучение разных длин волн весьма по-разному -- отсюда, в частности, и бальмеровский скачок, см. предыдущую задачу), а отрицательный ион водорода (см. задачу
и т. д. “ак почему же распределение энергии в спектре —олнца похоже на планковское? ѕо сути дела, причина этого в том, что атмосфера —олнца почти сера€, т.е. ослабл€ет проход€щее через нее излучение неселективно. Ёто вызвано тем, что основным источником непрозрачности газа в солнечной атмосфере €вл€етс€ не нейтральный водород, как у звезд класса A (последний поглощает излучение разных длин волн весьма по-разному -- отсюда, в частности, и бальмеровский скачок, см. предыдущую задачу), а отрицательный ион водорода (см. задачу  ). ќн поглощает видимое излучение всех длин волн почти одинаково. “емпература в солнечной атмосфере, точнее, в тех сло€х, которые мы непосредственно видим, различаетс€ не сильно и близка к 6000 K. ѕоэтому наблюдаемый спектр есть наложение планковских кривых со слегка различающимис€ температурами, вход€щими с весовыми множител€ми, учитывающими нейтральное, т.е. одинаковое дл€ всех длин волн ослабление излучени€ при прохождении им слоев атмосферы, лежащих над тем уровнем, где свет был излучен. ¬ результате и получаетс€, что спектр —олнца близок к чернотельному с
). ќн поглощает видимое излучение всех длин волн почти одинаково. “емпература в солнечной атмосфере, точнее, в тех сло€х, которые мы непосредственно видим, различаетс€ не сильно и близка к 6000 K. ѕоэтому наблюдаемый спектр есть наложение планковских кривых со слегка различающимис€ температурами, вход€щими с весовыми множител€ми, учитывающими нейтральное, т.е. одинаковое дл€ всех длин волн ослабление излучени€ при прохождении им слоев атмосферы, лежащих над тем уровнем, где свет был излучен. ¬ результате и получаетс€, что спектр —олнца близок к чернотельному с 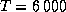 .
.
„то же касаетс€ ¬еги, то из-за более высокой температуры в ее атмосфере дол€ атомов водорода на возбужденных уровн€х больше, чем на —олнце. ќсновным источником поглощени€ становитс€ нейтральный водород, а не его отрицательный ион. ѕоглощение же водородом сильно селективно (см., в частности, задачу  ). Ќа разных длинах волн излучение приходит с сильно различающихс€ глубин, где температура заметно разна€. ¬ итоге спектр не похож на планковский.
). Ќа разных длинах волн излучение приходит с сильно различающихс€ глубин, где температура заметно разна€. ¬ итоге спектр не похож на планковский.
|
|
|
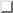 9.6 ¬близи кра€ диска луч зрени€ почти "скользит" по атмосферным сло€м, и поэтому излучение приходит к нам из самых поверхностных и потому самых холодных слоев атмосферы (соответствующую температуру обозначим через
9.6 ¬близи кра€ диска луч зрени€ почти "скользит" по атмосферным сло€м, и поэтому излучение приходит к нам из самых поверхностных и потому самых холодных слоев атмосферы (соответствующую температуру обозначим через 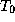 ). рай диска будет излучать как черное тело с
). рай диска будет излучать как черное тело с  . ¬ центре диска луч зрени€ направлен по нормали к атмосферным сло€м. ѕоэтому приход€щее к нам излучение зарождаетс€ в сравнительно глубоких сло€х атмосферы, где гор€чее (соответствующа€ температура
. ¬ центре диска луч зрени€ направлен по нормали к атмосферным сло€м. ѕоэтому приход€щее к нам излучение зарождаетс€ в сравнительно глубоких сло€х атмосферы, где гор€чее (соответствующа€ температура  ). »дущее из центра диска излучение будет близко к планковскому с
). »дущее из центра диска излучение будет близко к планковскому с 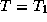 . “ак как
. “ак как 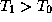 , то
, то  , т.е. центр диска €рче, чем край. ѕоскольку в серой атмосфере излучение всех длин волн ослабл€етс€ одинаково, глубина слоев, где излучение зарождаетс€, одна и та же. »наче говор€,
, т.е. центр диска €рче, чем край. ѕоскольку в серой атмосфере излучение всех длин волн ослабл€етс€ одинаково, глубина слоев, где излучение зарождаетс€, одна и та же. »наче говор€, 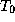 и
и  от
от  не завис€т. ќднако отсюда вовсе не следует, что отношение
не завис€т. ќднако отсюда вовсе не следует, что отношение  , дающее величину потемнени€ на краю, не зависит от
, дающее величину потемнени€ на краю, не зависит от  . ѕоскольку
. ѕоскольку  отличаетс€ от
отличаетс€ от 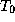 не сильно, это отношение легко получить в €вном виде, воспользовавшись результатом из задачи
не сильно, это отношение легко получить в €вном виде, воспользовавшись результатом из задачи 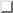 :
:

где
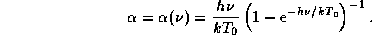
ќтсюда видно, во-первых, что величина потемнени€ к краю определ€етс€ градиентом температуры в атмосфере: чем быстрее температура растет с глубиной, тем больше отличие  от
от 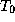 , а как следствие -- больше и потемнение. ѕри фиксированном градиенте температуры, т.е. при фиксированном отношении
, а как следствие -- больше и потемнение. ѕри фиксированном градиенте температуры, т.е. при фиксированном отношении 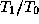 , потемнение в разных участках спектра оказываетс€ различным из-за различий в значении показател€
, потемнение в разных участках спектра оказываетс€ различным из-за различий в значении показател€ 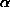 . ¬ рэлей-джинсовской (длинноволновой) области (
. ¬ рэлей-джинсовской (длинноволновой) области (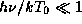 ) отношение €ркостей центр: край равно
) отношение €ркостей центр: край равно 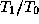 . ¬ виновской же области мы имеем
. ¬ виновской же области мы имеем 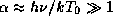 , так что потемнение существенно больше и увеличиваетс€ при переходе к более коротким длинам волн.
, так что потемнение существенно больше и увеличиваетс€ при переходе к более коротким длинам волн.
 9.7 ќтвет неожиданный: масса атмосферы возрастет примерно в 10 раз! ѕоймем, почему так. ќсновным источником непрозрачности газа солнечной атмосферы служат присутствующие в ней в качестве ничтожной примеси отрицательные ионы водорода (см. задачу
9.7 ќтвет неожиданный: масса атмосферы возрастет примерно в 10 раз! ѕоймем, почему так. ќсновным источником непрозрачности газа солнечной атмосферы служат присутствующие в ней в качестве ничтожной примеси отрицательные ионы водорода (см. задачу  ). ќни возникают путем присоединени€ к имеющимс€ в изобилии нейтральным атомам водорода свободных электронов, по€вл€ющихс€ при ионизации атомов "металлов". ≈сли содержание "металлов", €вл€ющихс€ донорами электронов, уменьшить на пор€док, примерно во столько же раз уменьшитс€ и содержание отрицательных ионов водорода. »з-за этого прозрачность газа возрастет на пор€док и станут видны более глубокие слои, так что масса атмосферы увеличитс€.
). ќни возникают путем присоединени€ к имеющимс€ в изобилии нейтральным атомам водорода свободных электронов, по€вл€ющихс€ при ионизации атомов "металлов". ≈сли содержание "металлов", €вл€ющихс€ донорами электронов, уменьшить на пор€док, примерно во столько же раз уменьшитс€ и содержание отрицательных ионов водорода. »з-за этого прозрачность газа возрастет на пор€док и станут видны более глубокие слои, так что масса атмосферы увеличитс€.
—олнце
 10.1 »нтересный вопрос, правда? ак это ни странно, ни в одном известном нам руководстве по астрофизике ни самого вопроса, ни пр€мого ответа на него не найти.
10.1 »нтересный вопрос, правда? ак это ни странно, ни в одном известном нам руководстве по астрофизике ни самого вопроса, ни пр€мого ответа на него не найти.
ћожно считать, что дл€ газа солнечной атмосферы выполн€етс€ закон ирхгофа: отношение излучательной способности газа 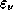 к его поглощательной способности
к его поглощательной способности 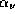 равно функции ѕланка
равно функции ѕланка  , так что
, так что

ќтсюда непосредственно следует, что тот агент, который сильнее всего поглощает, одновременно и сильнее всего излучает. ¬ солнечной атмосфере фотоны видимой части спектра сильнее всего поглощаютс€ отрицательными ионами водорода, вызыва€ их "фотоионизацию", точнее, "фотонейтрализацию", т.е. отрыва€ от отрицательного иона второй электрон и тем самым превраща€ его в обычный атом водорода. ѕри обратном процессе, т.е. при присоединении второго электрона к нейтральному атому водорода, и рождаютс€ фотоны дневного света. ƒонорами электронов, участвующих в этом процессе, служат атомы присутствующих в солнечной атмосфере в виде малых примесей "металлов". —ами они при этом, естественно, превращаютс€ в положительные ионы. ‘отоны, излучаемые при образовании отрицательных ионов водорода, принадлежат непрерывному спектру, так как захват происходит на единственный имеющийс€ у отрицательного иона св€занный уровень (энерги€ св€зи 0.75 э¬), а кинетические энергии захватываемых свободных электронов могут быть разными.
—огласитесь, что описанный только что механизм, которому об€зан своим рождением обычный дневной свет, довольно-таки экзотичен. Ќеудивительно, что пон€ли это далеко не сразу. ”же было установлено, какие термо€дерные реакции обеспечивают звезды энергией -- а тайна происхождени€ дневного света все еще оставалась нераскрытой.
|
|
|
 10.2 ѕо закону —тефана-Ѕольцмана поток излучени€ с поверхности абсолютно черного тела пропорционален четвертой степени температуры. –аспределение энергии в спектрах —олнца и солнечного п€тна близко к чернотельному. ѕоэтому искомое отношение потоков есть
10.2 ѕо закону —тефана-Ѕольцмана поток излучени€ с поверхности абсолютно черного тела пропорционален четвертой степени температуры. –аспределение энергии в спектрах —олнца и солнечного п€тна близко к чернотельному. ѕоэтому искомое отношение потоков есть
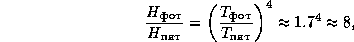
где использовано значение температуры тени п€тна  K и стандартное значение эффективной температуры (фотосферы) —олнца
K и стандартное значение эффективной температуры (фотосферы) —олнца  K. “аким образом, п€тна лишь на пор€док менее €рки, чем окружающа€ фотосфера, и они кажутс€ черными лишь по контрасту с ней. «акрытый гигантским п€тном диск —олнца осталс€ бы ослепительно €рким!
K. “аким образом, п€тна лишь на пор€док менее €рки, чем окружающа€ фотосфера, и они кажутс€ черными лишь по контрасту с ней. «акрытый гигантским п€тном диск —олнца осталс€ бы ослепительно €рким!
¬ приведенном решении есть существенна€ неточность. ћы нашли отношение интегральных потоков излучени€. Ќо максимум в спектре —олнца, закрытого п€тном, сместитс€ из видимой в инфракрасную область, и потоки излучени€ п€тна и спокойной фотосферы в видимой области будут различатьс€ больше, чем в 8 раз. (ћы уже сталкивались с подобным эффектом, например, в задаче 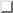 .)
.)
¬от более аккуратное решение. ћаксимум чувствительности глаза (
 ) практически совпадает с максимумом в распределении энергии в спектре —олнца, а дл€ него
) практически совпадает с максимумом в распределении энергии в спектре —олнца, а дл€ него 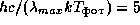 (см. задачу
(см. задачу 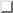 ; распределение энергии в спектре мы считаем чернотельным и пользуемс€ приближением ¬ина). ѕоэтому, учитыва€, что
; распределение энергии в спектре мы считаем чернотельным и пользуемс€ приближением ¬ина). ѕоэтому, учитыва€, что  , мы имеем
, мы имеем
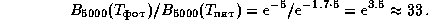
»так, в области максимума чувствительности глаза, т.е. в полосе V, блеск —олнца уменьшитс€ на 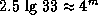 . ≈го видима€ звездна€ величина окажетс€ примерно на
. ≈го видима€ звездна€ величина окажетс€ примерно на 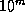 меньше, чем у Ћуны в полнолуние, так что освещенность все еще останетс€ в
меньше, чем у Ћуны в полнолуние, так что освещенность все еще останетс€ в 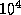 раз выше, чем в лунную ночь. √лавное, на что вы сразу же обратили бы внимание, это вовсе не то, что на улице стало бы темно, -- этого не произойдет, -- а то, что —олнце стало бы кроваво-красным.
раз выше, чем в лунную ночь. √лавное, на что вы сразу же обратили бы внимание, это вовсе не то, что на улице стало бы темно, -- этого не произойдет, -- а то, что —олнце стало бы кроваво-красным.
 10.3 ƒостаточно показать, что средн€€ теплова€ скорость электронов в короне превышает вторую космическую скорость дл€ —олнца. ƒействительно, при температуре солнечной короны
10.3 ƒостаточно показать, что средн€€ теплова€ скорость электронов в короне превышает вторую космическую скорость дл€ —олнца. ƒействительно, при температуре солнечной короны  K теплова€ скорость электронов равна
K теплова€ скорость электронов равна
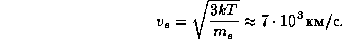
«десь 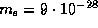 г -- масса электрона. ¬тора€ же космическа€ скорость дл€ —олнца равна
г -- масса электрона. ¬тора€ же космическа€ скорость дл€ —олнца равна
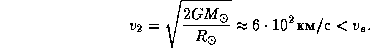
“ак что же, если не гравитаци€, все же удерживает электроны в короне? Ёто кулонова сила прит€жени€ к протонам, преп€тствующа€ по€влению объемных зар€дов. ѕротоны же гораздо т€желее электронов, и они удерживаютс€ гравитацией.
 10.4 ћожно представить себе, что в солнечной короне есть микроскопические зеркала-электроны, площадь каждого из которых равна
10.4 ћожно представить себе, что в солнечной короне есть микроскопические зеркала-электроны, площадь каждого из которых равна  см 2 (так называемое томсоновское сечение рассе€ни€). “огда полное число электронов в короне
см 2 (так называемое томсоновское сечение рассе€ни€). “огда полное число электронов в короне 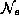 можно оценить из услови€
можно оценить из услови€ 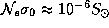 , где
, где  -- площадь поверхности —олнца. ѕредположим, что корона состоит из чистого водорода, который из-за ее высокой температуры
-- площадь поверхности —олнца. ѕредположим, что корона состоит из чистого водорода, который из-за ее высокой температуры  K) полностью ионизован. “огда получаем следующую оценку массы короны:
K) полностью ионизован. “огда получаем следующую оценку массы короны:
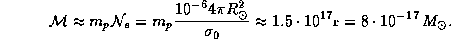
ѕо любым астрономическим меркам это ничтожна€ масса. ќна на четыре с лишним пор€дка меньше массы земной атмосферы (см. задачу  ).
).
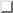 10.5 —корость протонов оценим, поделив рассто€ние, пройденное ими (1 а.е.), на врем€, проведенное в пути (
10.5 —корость протонов оценим, поделив рассто€ние, пройденное ими (1 а.е.), на врем€, проведенное в пути (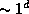 ):
):
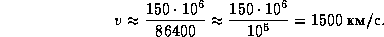
“акой скорости соответствует кинетическа€ энерги€ протонов  эрг, или пор€дка 10 кэ¬.
эрг, или пор€дка 10 кэ¬.
ѕон€тно, что близ поверхности —олнца энерги€ частиц была больше и двигались они быстрее, так как часть своей кинетической энергии частицы должны были затратить на отрыв от —олнца, т.е. на выход из его гравитационной потенциальной €мы. ѕочему это можно было не учитывать?






