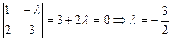К элементарным преобразованиям матриц относятся следующие:
1) умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число.
2) прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца) умноженные на одно и то же число;
3) перестановка местами строк (столбцов) матрицы;
4) отбрасывание нулевой строки (столбца);
5) замена строк матрицы соответствующими столбцами.
Определение 29: Матрицы, получающиеся одна из другой, при элементарных преобразованиях называется эквивалентными матрицами, обозначаются “ ~“
Основное свойство эквивалентных матриц:Ранги эквивалентных матриц равны.
Пример 18: Вычислить r(A), 
Решение: Первую строку умножим поэтапно на (-4)(-2)
(-7) и затем прибавим соответственно к второй, третьей и четвертой строкам.
~ 
поменяем местами вторую и четвертую строки 
вторую строку умножим на (-2) и прибавим к четвертой строке; сложим вторую и третью строки.
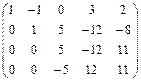сложим третью и четвертую строки.
~ 
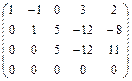откинем нулевую строку
~ 
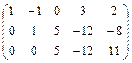r(A)=3 
ранг исходной матрицы
равен трем.
Определение 30: Назовем матрицу А ступенчатой, если все элементы главной диагонали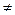 
0, а элементы под главной диагональю равны нулю.
Предложение:
1) ранг ступенчатой матрицы равен числу ее строк;
2) всякая матрица может быть приведена к ступенчатому виду с помощью элементарных преобразований.
Пример 19: При каких значениях l матрица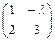 
имеет ранг, равный единице?
Решение: Ранг равен единице, если определитель второго порядка равен нулю, т.е.
