Механическое напряжение. Закон Гука, относительное удлинение, виды деформации, пластичность.
Виды деформации
Деформации растяжения и сжатия. Если к однородному, закрепленному с одного конца стержню приложить силу F вдоль его оси в направлении от стержня, то он подвергнется деформации растяжения. Деформацию растяжения испытывают тросы, канаты, цепи в подъемных устройствах, стяжки между вагонами и т. д. Если на закрепленный стержень подействовать силой вдоль его оси по направлению к стержню, то он подвергнется сжатию. Деформацию сжатия испытывают столбы, колонны, стены, фундаменты зданий и т. п. При растяжении или сжатии изменяется площадь поперечного сечения тела.
Деформация сдвига. Деформацию сдвига можно наглядно продемонстрировать на модели твердого тела, представляющего собой ряд параллельных пластин, соединенных между собой пружинами. Горизонтальная сила F сдвигает пластины друг относительно друга без изменения объема тела. У реальных твердых тел при деформации сдвига объем также не изменяется. Деформации сдвига подвержены заклепки и болты, скрепляющие части мостовых ферм, балки в местах опор и др. Сдвиг на большие углы может привести к разрушению тела – срезу. Срез происходит при работе ножниц, долота, зубила, зубьев пилы и т. д.
Деформация изгиба. Легко согнуть стальную или деревянную линейку руками или с помощью какой-либо другой силы. Балки и стержни, расположенные горизонтально, под действием силы тяжести или нагрузок прогибаются – подвергаются деформации изгиба. Деформацию изгиба можно свести к деформации неравномерного растяжения и сжатия. Действительно, на выпуклой стороне материал подвергается растяжению, а на вогнутой – сжатию. Причем чем ближе рассматриваемый слой к среднему слою KN, тем растяжение и сжатие становятся меньше. Слой KN, не испытывающий растяжения или сжатия, называется нейтральным. Так как слои АВ и CD подвержены наибольшей информации растяжения и сжатия, то в них возникают наибольшие силы упругости. От внешнего слоя к нейтральному эти силы уменьшаются. Внутренний слой не испытывает заметных деформаций и не противодействует внешним силам, а поэтому является лишним в конструкции. Его обычно удаляют, заменяя стержни трубами, а бруски – тавровыми балками. Сама природа в процессе эволюции наделила человека и животных трубчатыми костями конечностей и сделала стебли злаков трубчатыми, сочетая экономию материала с прочностью и меткостью «конструкций».
Деформация кручения. Если на стержень, один из концов которого закреплен, подействовать парой сил, лежащей в плоскости поперечного сечения стержня, то он закручивается. Возникает, как говорят, деформация кручения.
Каждое поперечное сечение поворачивается относительно другого вокруг оси стержня на некоторый угол. Расстояние между сечениями не меняется. Таким образом, опыт показывает, что при кручении стержень можно представить как систему жестких кружков, насаженных центрами на общую ось. Кружки эти (точнее, сечения) поворачиваются на различные углы в зависимости от их расстояния до закрепленного конца. Слои поворачиваются, но на различные углы. Однако при этом соседние слои поворачиваются друг относительно друга одинаково вдоль всего стержня. Деформацию кручения можно рассматривать как неоднородный сдвиг. Неоднородность сдвига выражается в том, что деформация сдвига изменяется вдоль радиуса стержня. На оси деформация отсутствует, а на периферии она максимальна. На самом удаленном от закрепленного конца торце стержня угол поворота наибольший. Его называют углом кручения. Кручение испытывают валы всех машин, винты, отвертки и т. п. Основными деформациями являются деформации растяжения (сжатия) и сдвига. При деформации изгиба происходит неоднородное растяжение и сжатие, а при деформации кручения – неоднородный сдвиг.
Абсолютное и относительное удлинения
Линейная деформация (деформация растяжения) – деформация, при которой происходит изменение только одного линейного размера тела.
Количественно она характеризуется абсолютным Δl и относительным ε удлинением.

где Δl – абсолютное удлинение (м); l и l0 – конечная и начальная длина тела (м).
- Если тело растягивают, то l > l0 и Δl = l – l0;
- если тело сжимают, то l < l0 и Δl = –(l – l0) = l0 – l
 или
или 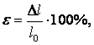
где ε – относительное удлинение тела (%); Δl – абсолютное удлинение тела (м); l0 –начальная длина тела (м).
5. Закон Гука
Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид

где Fупр – модуль силы упругости, возникающей в теле при деформации (Н); Δl – абсолютное удлинение тела (м).
Коэффициент k называется жесткостью тела – коэффициент пропорциональности между деформирующей силой и деформацией в законе Гука.
Жесткость пружины численно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.
В системе СИ жесткость измеряется в ньютонах на метр (Н/м):

Коэффициент жесткости зависит от формы и размеров тела, а также от материала.
Закон Гука для одностороннего растяжения (сжатия) формулируют так:
сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.
Механическое напряжение.
Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением.
Механическое напряжение s равно отношению модуля силы упругости Fупр к площади поперечного сечения тела S:

Измеряется механическое напряжение в Па: 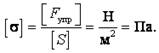
Наблюдения показывают, что при небольших деформациях механическое напряжение s пропорционально относительному удлинению e:
Эта формула является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным.
Коэффициент пропорциональности Е в законе Гука называется модулем упругости (модулем Юнга). Экспериментально установлено, что
модуль Юнга численно равен такому механическому напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза.
Докажем это: Из закона Гука получаем, что  Если модуль Юнга E численно равен механическому напряжению σ, то
Если модуль Юнга E численно равен механическому напряжению σ, то  .
.
Измеряется модуль Юнга в Па: 
Практически любое тело (кроме резины) при упругой деформации не может удвоить свою длину: значительно раньше оно разорвется. Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l0, S, F). Таким образом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия.
Закон Гука, записанный в форме (2), легко привести к виду (1). Действительно, подставив в (2)  и
и  , получим:
, получим:
 или
или 
где 
Пластичность.
Тело из любого материала при малых деформациях ведет себя как упругое. В то же время почти все тела в той или иной мере могут испытывать пластические деформации. Существуют хрупкие тела.
Механические свойства материалов разнообразны. Такие материалы, как резина или сталь, обнаруживают упругие свойства до сравнительно больших напряжений и деформаций. Для стали, например, закон Гука выполняется вплоть до = 1%, а для резины – до значительно больших , порядка десятков процентов. Поэтому такие материалы называют упругими.
У мокрой глины, пластилина или свинца область упругих деформаций мала. Материалы, у которых незначительные нагрузки вызывают пластические деформации, называют пластичными.
Деление материалов на упругие и пластичные в значительной мере условно. В зависимости от возникающих напряжений один и тот же материал будет вести себя или как упругий, или как пластичный. Так, при очень больших напряжениях сталь обнаруживает пластичные свойства. Это широко используют при штамповке стальных изделий с помощью прессов, создающих огромную нагрузку.
Холодная сталь или железо с трудом поддаются ковке молотом. Но после сильного нагрева им легко придать посредством ковки любую форму. Пластичный при комнатной температуре свинец приобретает ярко выраженные упругие свойства, если его охладить до температуры ниже –100°С.
Большое значение на практике имеет свойство твердых тел, называемое хрупкостью. Тело называют хрупким, если оно разрушается при небольших деформациях. Изделия из стекла и фарфора хрупкие: они разбиваются на куски при падении на пол даже с небольшой высоты. Чугун, мрамор, янтарь также обладают повышенной хрупкостью. Наоборот, сталь, медь, свинец не являются хрупкими.
Отличительные особенности хрупких тел легче всего уяснить с помощью зависимости от при растяжении. На рисунке 11, а, б изображены диаграммы растяжений чугуна и стали. На них видно, что при растяжении чугуна всего лишь на 0,1% в нем возникает напряжение около 80 МПа, тогда как в стали оно при такой же деформации равно лишь 20 МПа.
Чугун разрушается сразу при удлинении на 0,45%, почти не испытывая предварительно пластических деформаций. Предел прочности его равен 1,2∙108 Па. У стали же при ε = 0,45% деформация все еще остается упругой и разрушение происходит при ≈ 15%. Предел прочности стали равен 700 МПа.






