Пластичность – способность материала без разрушения получать большие остаточные деформации.
Хрупкость – способность материала разрушаться при очень малых остаточных деформациях.
Две основные характеристики пластичности:
1) относительное удлинение образца при разрыве,
2) относительное сужение поперечного сечения образца при разрыве.
Относительное удлинение образца при разрыве – отношение абсолютного удлинения образца при разрыве к его первоначальной длине (рис. 14):
где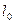 
– длина расчетной части образца до начала нагружения (первоначальная длина); 
– суммарная длина обоих участков расчетной части образца после разрыва.
Рис. 14. Определение относительного удлинения образца при разрыве
Величину можно определить по формуле для вычисления 
, предварительно определив по диаграмме. Экспериментально находят, сложив обе части разорванного образца по месту разрыва и измерив штангенциркулем длину между нанесёнными до проведения испытаний рисками.
Рис. 15. Определение суммарной длины обоих участков расчетной части образца после разрыва и диаметра шейки в месте разрыва
Условно принято, что если 
то материал пластичный (малоуглеродистая сталь, алюминий, латунь), а если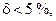 
то хрупкий (чугун, высокоуглеродистая инструментальная сталь).
Относительное сужение поперечного сечения образца при разрыве – отношение абсолютного уменьшения площади поперечного сечения образца при разрыве к его первоначальной площади:
где 
– первоначальная площадь поперечного сечения образца (
– начальный диаметр расчетной части образца);
– конечная площадь поперечного сечения шейки образца после разрыва (
–диаметр шейки образца в месте разрыва).
Диаграмма растяжения хрупкого материала (чугун, высокоуглеродистая сталь) не имеет площадки текучести и зоны упрочнения (рис. 16). Шейка на образце из хрупкого материала не образуется. Поэтому основная механическая характеристика хрупкого материала – предел прочности 
.
Рис. 16. Диаграмма растяжения хрупкого материала
Контрольные вопросы
1. Дайте определение центрального растяжения (сжатия) стержня.
2. Сформулируйте правило знаков при центральном растяжении (сжатии).
3. Что такое абсолютная продольная деформация стержня?
4. Что такое относительная продольная деформация стержня?
5. Дайте определение относительной поперечной деформации стержня.
6. Напишите формулу, выражающую зависимость между относительной поперечной и относительной продольной деформацией.
7. Что называют коэффициентом Пуассона?
8. В каких пределах изменяется коэффициент Пуассона для изотропных материалов? В каких пределах находятся его значения для большинства металлов и сплавов?
9. Сформулируйте закон Гука. Границы применимости закона Гука.
10. В каких пределах изменяется модуль Юнга для сталей?
11. По какой формуле определяются нормальные напряжения при растяжении (сжатии)?
12. По какой формуле определяется абсолютное удлинение однородного стержня при постоянной нормальной силе и постоянной площади сечения?
13. При каких условиях проводятся испытания на растяжение?
14. Как выглядят образцы для испытаний на растяжение?
15. С какой целью диаграмму растяжения вида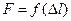 
перестраивают в диаграмму 
?
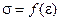16. Нарисуйте диаграмму растяжения малоуглеродистой стали. Назовите все участки диаграммы растяжения малоуглеродистой стали.
17. Какие относительные продольные деформации называют упругими, а какие – пластическими?
18. Что такое предел пропорциональности?
19. Что такое предел упругости?
20. Что такое предел текучести?
21. Для каких материалов наблюдается отсутствие площадки текучести? Как выглядит при этом диаграмма растяжения?
22. Что такое условный предел текучести? Когда используют это понятие?
23. Чем объясняется появление на образце линий Чернова – Людерса?
24. В чём состоит суть процесса образования пластических деформаций?
25. Что такое предел прочности?
26. Образец был нагружен до точки К, лежащей на площадке текучести диаграммы растяжения малоуглеродистой стали, а затем разгружен. Покажите, как пройдет линия разгрузки? Покажите на этой диаграмме упругие и пластические относительные продольные деформации?
27. Образец был нагружен до точки К, лежащей в зоне упрочнения диаграммы растяжения малоуглеродистой стали, а затем разгружен. Покажите, как пройдет линия разгрузки? Покажите на этой диаграмме упругие и пластические относительные продольные деформации?
28. Чем диаграмма растяжения малоуглеродистой стали отличается от диаграммы сжатия малоуглеродистой стали? Как происходит сжатие пластичного образца, растяжение пластичного образца?
29. Чем отличаются диаграммы растяжения пластичного и хрупкого материалов и почему?
30. Чем отличаются диаграммы сжатия пластичного и хрупкого материалов и почему?
31. Чем отличаются диаграммы растяжения и сжатия хрупкого образца?
32. Образец был нагружен до точки К, лежащей в зоне упрочнения диаграммы растяжения малоуглеродистой стали, затем разгружен, а потом снова нагружен. Как видоизменится диаграмма растяжения при повторном нагружении образца?
33. В чем заключается явление наклёпа?
34. Объясните явление наклепа с помощью диаграммы растяжения малоуглеродистой стали.
35. Дайте определения понятиям «пластичность», «хрупкость».
36. Какие показатели пластичности вы знаете? Напишите формулы для их вычисления.
Порядок проведения работы
1. Замерить штангенциркулем начальные размеры рабочей части образца: диаметр и длину, подсчитать начальную площадь поперечного сечения .
2. Поместить образец в захваты испытательной машины.
3. Включить машину. Плавно увеличивая нагрузку, довести образец до разрушения.
4. Снять диаграмму растяжения с диаграммного аппарата.
5. Подсчитать с учётом масштаба значения усилий:
Fпц – продольная сила при пределе пропорциональности;
Fт – продольная сила при пределе текучести;
Fmax – продольная сила при пределе прочности;
Fр – продольная сила при разрыве образца.
Разделив значения этих усилий на 
– первоначальную площадь образца, определить значения σпц, σт, σB, σр.
6. Подсчитать с учётом масштаба значения абсолютных деформаций:
∆ l пц – продольная сила при пределе пропорциональности;
∆ l т – продольная сила при пределе текучести;
∆ l в – продольная сила при пределе прочности;
∆ l р – продольная сила при разрыве образца.
Разделив значения этих абсолютных деформаций на 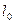– начальную расчетную длину образца, определить соответствующие относительные продольные деформации 
, 
, 
, 
.
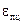7. Определить модуль Юнга, разделив σпцна .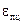
8. Выбрав произвольную точку К в зоне упрочнения диаграммы растяжения и предположив, что нагрузка образца проводится до этой точки, построить линию разгрузки. Определить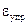 
–упругую деформацию, 
– остаточную (пластическую) деформацию, 
– полную относительную продольную деформацию.
9. Из точки D, соответствующей разрыву образца, провести прямую DL, параллельную начальному участку ОА, до пересечения с осью абсцисс. Измерив отрезок ОL, определить – относительное удлинение образца при разрыве.
10. Вынуть части разорванного образца из захватов испытательной машины. Сложить обе части разорванного образца по месту разрыва и измерить – суммарную длину обоих участков расчетной части образца после разрыва и – диаметр шейки в месте разрыва. Найти относительное сужение поперечного сечения образца при разрыве 
.
СПИСОК ЛИТЕРАТУРЫ
Буланов Э.А., Тарасов А.С., Зубарев А.А. Лабораторный практикум по курсу «Прикладная механика». Раздел «Сопротивление материалов». – М.: МГТУ им. А.Н. Косыгина, 2001. – 31 с.
Дарков А.В., Шпиро Г.С. Сопротивление материалов: Учеб. для техн. вузов. - 5-е изд., перераб. и доп. – М.: Высш. шк., 1989. – 624 с.
Епифанов А.П., Морозов А.Н. Виртуальные лабораторные работы по сопротивлению материалов и прикладной механике. – Красноярск: КФ ИрГУПС, 2005. – 34 с.
Ицкович Г.М. Сопротивление материалов: Учеб. для техникумов. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1970. – 488 с.
Карцов С.К. Журнал лабораторных работ по курсу «Сопротивление материалов». – М.: МАДИ (ГТУ), 2007. – 17 с.
Морозов А.Н. Лабораторный практикум по сопротивлению материалов и прикладной механике. – Красноярск: КФ ИрГУПС, 2003. – 82 с.
Сопротивление материалов. Под ред. А.Ф. Смирнова: Учеб. для вузов. – 3-е изд., перераб. и доп. – М.: Высш. шк., 1975. – 480 с.
Стёпин П.А. Сопротивление материалов: Учеб. для вузов. – 7-е изд. – М.: Высш. шк., 1983. – 303 с.
Феодосьев В.И. Сопротивление материалов: Учеб. для вузов. – 10-е изд., перераб. и доп. - М.: Изд-во МГТУ им. Н. Э. Баумана, 2001. – 592 с.
Шинкин В.Н. Сопротивление материалов. Простые и сложные виды деформаций: Курс лекций. – М.: Издательский Дом МИСиС, 2008. – 307 с.
