“еорема1: ѕусть ƒ-ограниченна€ многосв€зна€ или односв€зна€ область с кусочно-гладкой границей  ; функци€ f(z) Цинтегрирована в
; функци€ f(z) Цинтегрирована в  †и аналетична в ƒ, тогда имеет место следующа€ формула
†и аналетична в ƒ, тогда имеет место следующа€ формула
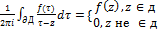 †Ц »нтегральна€ формула оши
†Ц »нтегральна€ формула оши

—мысл функции оши
«аметим, что в левую часть входит только точки 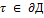 . » значени€ функции под интегралом беретс€ только в этих граничных точках. “аким образом значени€ функции внутри ƒ вполне определ€етс€ ее значени€ми на границе в ƒ.
. » значени€ функции под интегралом беретс€ только в этих граничных точках. “аким образом значени€ функции внутри ƒ вполне определ€етс€ ее значени€ми на границе в ƒ.
ќпределение 1: ≈сли  †Ц граница односв€зна или многосв€зна ограниченной области ƒ и функци€ f(z) аналетична в ƒ и непрерывна в ƒ, то интеграл
†Ц граница односв€зна или многосв€зна ограниченной области ƒ и функци€ f(z) аналетична в ƒ и непрерывна в ƒ, то интеграл
 †называетс€ интегралом оши.
†называетс€ интегралом оши.
ќпределение 2: ѕусть 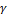 - кусочно-гладкий замкнутый или разомкнутый контур на котором задана непрерывна€ функци€
- кусочно-гладкий замкнутый или разомкнутый контур на котором задана непрерывна€ функци€ 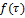 †интеграл
†интеграл
 †называетс€ интегралом оши
†называетс€ интегралом оши
“еорема 2: »нтеграл типа оши F(z)=†††  †есть однозначна€ аналетическа€ функци€ на множестве
†есть однозначна€ аналетическа€ функци€ на множестве  †причем n-а€ производно функции F(z)
†причем n-а€ производно функции F(z)
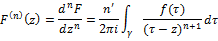
“еорема 3: (о бесконечной дифферинцируемости аналитической функции)
≈сли f(z) аналетична€ функци€ в ƒ, то она в этой области имеет производную всех пор€дков и эти производные сами €вл€ютс€ аналетичными функци€ми в этой облости.
ѕервообразна€ и интеграл в тфкп.
“еорема 1. ѕусть ф-и€ f (z) непрерывна в обл-и 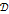 †тогда:
†тогда:  . “огда ф-и€ €в-с€ аналогичной ф-ей в обл.
. “огда ф-и€ €в-с€ аналогичной ф-ей в обл.  †и
†и  .
. 
ќпр 1. ‘-и€  †Ц называетс€ первообразной ф-иейf(z)
†Ц называетс€ первообразной ф-иейf(z)
“еорема 2. ≈сли  †Ц первообразные одной и той же ф-ии f (z), то
†Ц первообразные одной и той же ф-ии f (z), то 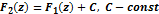 . все первообразные одной ф-ии f (z) отличаютс€ друг от друга на const -у
. все первообразные одной ф-ии f (z) отличаютс€ друг от друга на const -у
ќпр 2. ћножество всех первообразных называетс€ неопределенным интегралом и обозначаетс€ 
“еорема 3. (формула Ќьютона-Ћейбница). ѕусть ф-и€f(z) задана в обл. 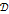 †и F(z) Ц одна из ее первообразных, тогда
†и F(z) Ц одна из ее первообразных, тогда  †Ц формула Ќьютона-Ћейбница.“очки
†Ц формула Ќьютона-Ћейбница.“очки 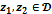
»нтеграл в ф.Ћейбница не зависит от пути интегрировани€. ј зависит олишь от значени€ первообразной в т. 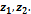
“еорема 4. ћорена. (обратна€ теорема к интегральной теореме оши).
≈сли f(z) интегрирована в односв€зной обл.  †и
†и  †где
†где 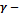 произвольный замкнутый контур лежащий в
произвольный замкнутый контур лежащий в  , то ф-и€ f(z) однозначно аналитична€ ф-и€ в обл.
, то ф-и€ f(z) однозначно аналитична€ ф-и€ в обл. 
–€д “ейлора
“еорема “ейлора 1: ѕусть функц. f (z) аналитична в области D, тогда ∀ т. 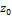 †из области D Ǝ окрестность(круг)
†из области D Ǝ окрестность(круг)
U ( 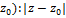 <
<  в которой функц. f (z) представлена в виде степенного р€да:
в которой функц. f (z) представлена в виде степенного р€да:
 †(1)
†(1)
где коэфф.  вычисл€етс€ по формулам:
вычисл€етс€ по формулам:
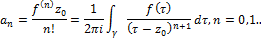
где  - произвольна€ окружность,
- произвольна€ окружность,  =
=  ,
,  <
< 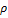 (
(

“еорема 2: ѕредставление функц. f (z) удовлетвор€ющей услови€м теоремы “ейлора в степенной р€д (1) единственно.
ќпр-е 1: –€д (1) назыв. р€дом “ейлора дл€ функц. f (z).
ќпр-е 2: ≈сли функц. f (z) в некоторой окрестности т. 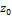 †представимо в виде р€да (1), то говор€т, что функц. f (z) регул€рна в т.
†представимо в виде р€да (1), то говор€т, что функц. f (z) регул€рна в т. 
“еорема 3: ‘ункц. f (z) регул€рна в области D  , когда она аналитична в этой области.
, когда она аналитична в этой области.
–адиус сходимости степенного р€да (1) вычисл€етс€ по формуле оши-јдамара:

ѕодзаголовок:
ќсновные разложени€ р€да “ейлора в окрестности т. ќ:


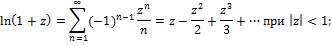

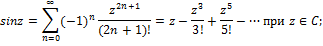
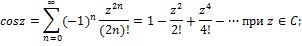
|
|
|
–€д Ћорана.
“еорема Ћорана: пусть f(z) анал-на и однозначна в пользе к: r<(z-z0)<R, в этом кольце f(z) представима в виде р€да
f(z)=∑ an (z-z0)n
коэф-ты вычисл€ютс€:
an=1/2πi ꭍ f(ч)/(ч-ч0)n+1 dч, n=±1, ±2Е
контур ꙋ - окружностьꙋ: (ч-z0)=ẟ, где чẟ<R
ќпределение 1: –€д (16-1) = р€дом Ћорана f(z)
f(z)=∑ an (z-z0)n + ∑ an (z-z0)n
глав.часть правильна€ часть
ќпределение 2: „асть р€да Ћорана, содержаща€ отрицательные степени n главной частью р€да Ћорана; остальна€ часть Ц правильной частью (n ≥ 0).
ѕредельные случаи кольца .
≈сли r=0, тогда - проколота€ R Ц окрест. в т. z0
R=∞ K Ц проколота€ окружность бесконечности
ќтличи€ р€да “ейлора от р€да Ћорана.
1. –€д “ейлора Ц частный случай р€д Ћорана (когда нет отриц. степеней);
2. –€д “ейлора имеет место в круге, в том числе и в центре круга дл€ Ћорана - это разложение в кольце, в центре которого он может расходитьс€;
3. ƒл€ коэффициентов р€да “ейлора есть формула через производную функции f(z) в точке to. ƒл€ коэффициентов р€да Ћорана такой формулы нет.
–€д Ћорана на бесконечности.
–азложение функции f(z) в р€д Ћорана в окрестности z=0
f(z)=∑ an (z-z0)n + ∑ an (z-z0)n
ƒл€ того, чтобы получить разложение функции в р€д Ћорана в окружности бесконечности, необходимо произвести замену z=1/t, z=0⇒ t= ∞
F(1/t)=g(t)
g(t)=∑ an (1/t)n + ∑ an (1/t)n=∑ antn + ∑ antn
т.е., не обраща€ внимани€ на обозначение Ц разложение функции f(z) =∑ anzn + ∑ anzn- разложение функции f(z)
n= -∞ (правильна€) n=1 (главна€ часть)
в р€д Ћорана на бесконечности.
–азложение функции f(z) в р€д Ћорана как в окрестности z=0, так и в окрестности z=∞ †одинаковые f(z) =∑ anzn, но главна€ и правильна€ части у этих разложений разное.
17. ќсобые точки аналитической функции.
ќпределение 1: “очка 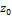 †в которой функци€ f(z) непрерывна или определена, но не €вл€етс€ аналетичной называетс€ особой точкой аналетичной функции f(z)
†в которой функци€ f(z) непрерывна или определена, но не €вл€етс€ аналетичной называетс€ особой точкой аналетичной функции f(z)
ќ“-особа€ точка
ќпределение 2: ќ“ называетс€ изолированна€ S, если 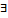 †окрестность этой точки в которой нет других ќ“-к.
†окрестность этой точки в которой нет других ќ“-к.
¬ противном случае ќ“ называетс€ неизолированной
»ќ“ Ц изолированна€ ќ“
Ќе»ќ“- неизолированна€ ќ“
ќпределение 3: »ќ“ называетс€ ќ“ однозначного характера, если в некоторой проколотой окрестности этой точки функци€ f(z) однозначна. в противном случае »ќ“ наз-с€ »ќ“ многозначного или неоднозначного характера.
≈сли число ќ“ конечно, то все эти точки изолированы. ≈сли ќ“ образуют бесконечное множество, то все предписанные точки этого множества будут неизолированы.
ѕусть  †»ќ“ однозначного характера функции f(z) по определению, это означает, что существует проколота€ окрестность этой точки в которой функци€ f(z) разлагаетс€ в р€д Ћорана.
†»ќ“ однозначного характера функции f(z) по определению, это означает, что существует проколота€ окрестность этой точки в которой функци€ f(z) разлагаетс€ в р€д Ћорана.
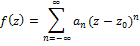
√лавна€ часть р€да Ћорана

ќпределение 4: »ќ“ однозначного характера  называетс€:
называетс€:
1 ”странимой ќ“ (”ќ“), если разложение функции в р€д Ћорана не содержит главную часть (гл.ч.=0)
2 ѕолюсом пор€дка m, если главна€ часть р€да Ћорана содержит конечное число отрицательных степеней причем наивысший пор€док отриц. степени =m
3 существенной ќ“ (—ќ“) если главна€ часть р€да Ћорана бесконечна
—хема ќ“
††††††††††††††††††††††††††††††††††††††††††††††††† ќ“ аналетичской функции f(z)
|
|
|
 |  |
†††††††††††††††††††††††††††††††††††††††††††††††††††††† »ќ“†††††††††††††††††††††† не»ќ“
 |  |
††††††††††† »ќ“ одинарного характера »ќ“ неодинарного характера
 |  |  | |||
ќ“полюс пор€дка m —ќ“
ѕример 1: 
 -ќ“, т.кf(0)
-ќ“, т.кf(0)  0
0
 -ќ“, т.кsinz
-ќ“, т.кsinz  †при
†при 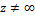

√лавна€часть р€да Ћорана =0

2 

√лавна€ часть р€да Ћорана =  †††††††††††
††††††††††† 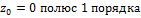
ќпределение 5: ѕолюс первого пор€дка называетс€ простым.
—войства ќ“
“еорема1. »ќ“ z0≠∞ однозначного характера дл€ функции f(z) будет ”ќ“. “огда и только тогда, когда ”ќ“ ⇔ 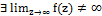 †.
†.
¬ свою очередь конечный предел f(z) при z →z0∃ тогда и только тогда, когда f(z) ограничена в некоторой проколотой окресности в точке z0.
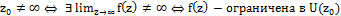 .
.
“еорема2. ≈сли z0≠∞ - ”ќ“ функции f(z), то эту функцию можно доопределить в точке z0 и получить функцию F(z) аналитическую в точке z0. —ледующим образом:

ѕример
f(z)=sinz/z;
z0=0-”ќ“.
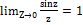 , устранили особенность в т. z=0
, устранили особенность в т. z=0
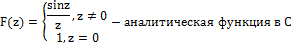
“еорема3. “очка z0 = ∞ - полюс пор€дка n дл€ функции f(z), тогда и только тогда, когда
 †и
†и 
“еорема4. z0≠∞ -—ќ“ функции f(z) тогда и только тогда, когда  †не существует.
†не существует.






