Развернутая форма записи числа

СИСТЕМЫ СЧИСЛЕНИЯ И

ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ В ДРУГУЮ

 

Система счисления (СС)- это способ представления чисел и соответствующие ему правила действий над ними.

 

Системы счисления делятся на позиционные и непозиционные

 

Название	Позиционные	Непозиционные
Определение	Значение цифры в записи числа зависит от её позиции	От положения знака в изображении числа не зависит величина которую он обозначает
Пример	Арабская десятичная	Римская   ССXXII
Алфавит	0 1 2 3 4 5 6 7 8 9
Основание	10	7

 

Основанием системы счисления - называют количество цифр используемых для записи чисел

                

Алфавитом СС - называют все цифры (знаки) используемые для записи чисел

 

Развернутая форма записи числа

Aq = a_na_n-1..a₁a₀ = a_n qⁿ + a_n-1 q^n-1 +..a₁ q¹ + a₀ q⁰

где

Aq - число

q - основание

a_i - цифры

n - количество разрядов целой части

m - количество разрядов дробной части

 

123,45₁₀=100+20+3+0,4+0,05=1∙10²+2∙10¹+3∙10⁰+4∙10^-1+5∙10^-2

123,45₈=1∙8²+2∙8¹+3∙8⁰+4∙8^-1+5∙8^-2

Таблица эквивалентов чисел

q=10	q=16	q=12	q=8	q=5	q=4	q=2
0	0	0	0	0	0	0
1	1	1	1	1	1	1
2	2	2	2	2	2	10
3	3	3	3	3	3	11
4	4	4	4	4	10	100
5	5	5	5	10	11	101
6	6	6	6	11	12	110
7	7	7	7	12	13	111
8	8	8	10	13	20	1000
9	9	9	11	14	21	1001
10	А	А	12	20	22	1010
11	В	В	13	21	23	1011
12	С	10	14	22	30	1100
13	D	11	15	23	31	1101
14	E	12	16	24	32	1110
15	F	13	17	30	33	1111
16	10	14	20	31	100	10000

                   Полужирным шрифтом выделены алфавиты в соответствующих системах счисления.

 

Правило перевода числа из любой системы счисления в десятичную

 

Чтобы перевести число в десятичную систему счисления надо:

1. записать число в развернутой форме

2. все цифры перевести в десятичную СС (для СС с q>10)

3. вычислить значение полученного выражения

 

123,45₈=1∙8²+2∙8¹+3∙8⁰+4∙8^-1+5∙8^-2=64+16+3+0,5+5/64=83,578₁₀

1BE,84₁₆=1∙16²+ B ∙16¹+ E ∙16⁰+8∙16^-1+4∙16^-2=

           =1∙16²+ 11 ∙16¹+ 14 ∙16⁰+8∙16^-1+4∙16^-2=

           =256+11∙16+14∙1+0,5+0,015=446,515₁₀

Решите примеры:

1) 15₆ = А₁₀

2) 150₆ = А₁₀

3) 15₈ = А₁₀

4) DF₁₈ = А₁₀

5) 1АВ₁₆ = А₁₀

 

 

Правило перевода целых десятичных чисел в другие системы счисления:

1. Последовательно выполнять деление с остатком данного числа и получаемых неполных частных на основание новой СС до тех пор пока не получим неполное частное, меньшее делителя.

2. Полученные остатки, являющиеся цифрами числа в новой СС, привести в соответствие с алфавитом новой СС (для СС с q>10)

3. Составить число в новой СС, записывая все остатки, начиная с последнего частного

1910 = 100112
1910 = 1316
20510 = CD16

 

Решите примеры:

1) 5₁₀= А₅ = А₈ = А₁₅ = А₁₈

2) 15₁₀= А₅ = А₈ = А₁₅ = А₁₈

1) 150₁₀= А₅ = А₈ = А₁₅ = А₁₈

Быстрый Перевод в двоичную систему счисления разложением на степени двойки

Перевод числа в двоичную СС для некоторых чисел удобно производить вторым способом: разложением на степени двойки. Конечно, для этого эти степени надо знать наизусть;-)

 

19₁₀ = 16 + 2 + 1 = 2⁴ + 2¹ + 2⁰=1∙2⁴ + 0∙2³ +0∙2² +1∙2¹ + 1∙2⁰ =10011₂

Можно пропустить развернутую форму записи числа. Если степень есть, то ставим единицу, если по порядку степени нет (в нашем примере 3 и 2), то там ставим 0.

19₁₀ = 16 + 2 + 1 = 2⁴ + 2¹ + 2⁰= 10011₂

Особенно удобен этот способ для чисел значение которых близко к степени.

Решите примеры:

1) 16₁₀ = А₂

1) 32₁₀ = А₂

1) 161₁₀ = А₂

1) 321₁₀ = А₂

1) 600₁₀ = А₂

Правило перевода двоичного числа в СС с основанием q=2ⁿ

1. данное двоичное число разбить начиная от запятой (целую и дробную части) на группы по n цифр в каждой

2. если в последних (крайних) группах окажется менее n разрядов, то их надо дополнить (с краю) незначащими нулями до нужного числа разрядов.

3. заменить каждую n-разрядную группу цифр соответствующей цифрой в СС основанием q=2ⁿ

 

Для перевода необходимо пользоваться таблицей эквивалентов чисел.

 

 

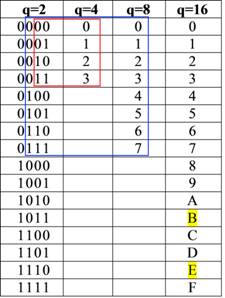
Решите примеры:

1) 1110100₂ = А₄ = А₈ = А₁₆

2) 11110000₂ = А₄ = А₈ = А₁₆

3) 10101010₂ = А₄ = А₈ = А₁₆

 

Правило перевода  чисел в СС с основанием q=2ⁿ в двоичную СС

Чтобы число из СС с основанием q=2ⁿ перевести в двоичную СС, надо каждую цифру этого числа заменить её n-разрядным эквивалентом в двоичной СС.

Решите примеры:

1) 3201₄ = А₂ = А₁₆

2) 3201₈ = А₂ = А₁₆

3) 3201₁₆ = А₂ = А₈

4) FAC₁₆ = А₂ = А₈