По известному дирекционному углу a n и по исправленным горизонтальным углам b испр вычисляются дирекционные углы остальных сторон теодолитного хода по формулам для правых горизонтальных углов:
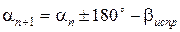– дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус исправленный горизонтальный угол правый по ходу.
Величина дирекционного угла не может превышать 360° и быть меньше 0°. Если величина дирекционного угла больше 360°, то из результата вычислений необходимо вычесть 360° (см. пример).
Контроль вычисления дирекционных углов. В замкнутом теодолитном ходе в результате вычислений получается дирекционный угол исходной стороны.
Пример вычисления дирекционных углов:
Дирекционный угол исходной стороны a1-2 равен 45°45¢.
;
;
;
;
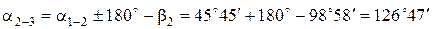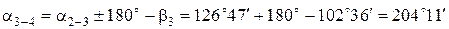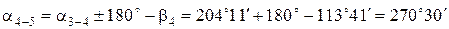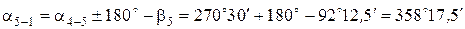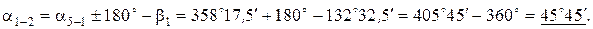При вычислении дирекционного угла получилось значение 405°45 ¢. Из полученного значения вычитается 360°.
.
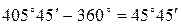Контроль вычисления дирекционных углов получился.
Все результаты вычислений заносятся в таблицу «Ведомость вычисления координат» (табл. 2).
1.3 Вычисление приращений координат
Вычисление приращений координат выполняется по формулам:
,
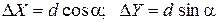где d – горизонтальное проложение (длина) линии; a – дирекционный угол этой линии.
Приращения координат вычисляются с точностью два знака после запятой.
Пример вычисления приращений координат:
;
;
;
;
.
;
;
;
;
.
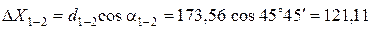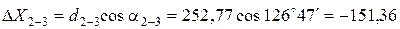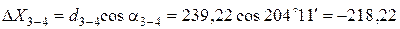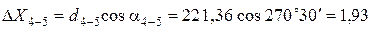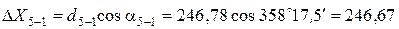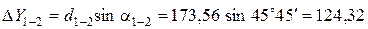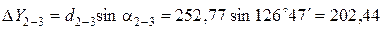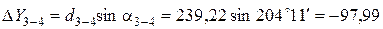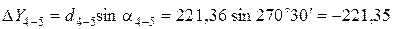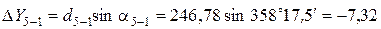Все результаты вычисления заносятся в табл. 2. Пример вычисления тригонометрических функций на калькуляторе приведен в отдельном файле.
1.4 Уравнивание линейных измерений
Разность между суммой вычисленных приращений координат и теоретической суммой называется линейной невязкой хода и обозначается fХ и fY. Уравнивание линейных измерений выполняется по осям Х и Y.
Линейная невязка вычисляется по формулам:
.
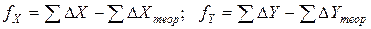Теоретическая сумма приращений координат зависит от геометрии хода. В замкнутом теодолитном ходе она равна нулю, тогда невязка равна
.
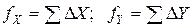Прежде, чем распределять невязки в приращения координат, необходимо убедиться в их допустимости. Для чего вычисляется абсолютная невязка хода fабс
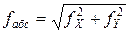
и относительная
,
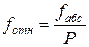где Р – периметр хода (сумма длин сторон), м.
Относительная невязка сравнивается с допустимой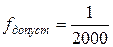 
.
В случае, когда полученная относительная невязка допустима, т.е.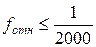 
, то вычисляются поправки в приращения координат пропорционально длинам сторон. Невязки распределяются с обратным знаком. Если 
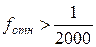, то проверяются вычисления в п. 3.3 и 3.4.
Поправки в приращения координат d X и d Y вычисляются по формулам с округлением до 0,01 м:
,
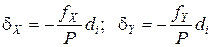где dX и dY – поправка в приращение по оси Х и Y, соответственно, м; fX и fY – невязки по осям, м; Р – периметр (сумма сторон), м; di – измеренная длина (горизонтальное проложение), м.
Знак у поправки противоположен знаку невязки. Поправки записываются в «Ведомость вычисления координат». В примере (табл. 6) поправки показаны красным цветом.
После вычисления поправок следует сделать проверку, т.е. сложить все поправки. Если их сумма будет равна невязке с обратным знаком, то распределение невязки выполнено правильно. То есть:
.
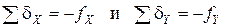Вычисляются исправленные приращения.
Полученные поправки алгебраически прибавляются к соответствующим приращениям и получаются исправленные приращения:
.
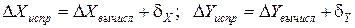Контроль: сумма исправленных приращений в замкнутом теодолитном ходе должна равняться нулю, т.е. должно выполняться равенство:
.
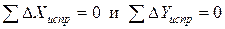Пример вычисления линейной невязки:
;
.
;
.
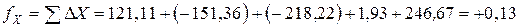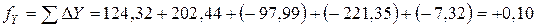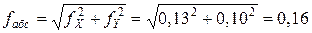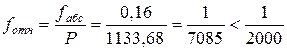Пример вычисления поправок в приращения координат:
;
;
;
;
;
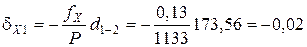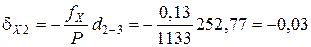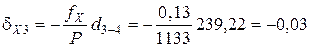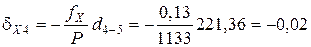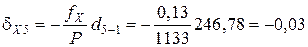Контроль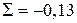 
.
;
;
;
;
;
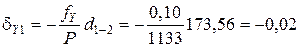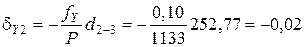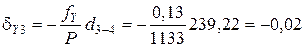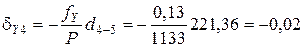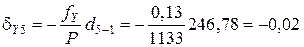Контроль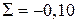 
.
Поправки записываются в «Ведомость вычисления координат» над вычисленными приращениями. В примере поправки показаны красным цветом (Табл. 2).
Пример вычисления исправленных приращений координат:
.
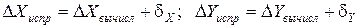Исправленные приращения:
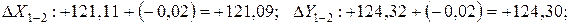
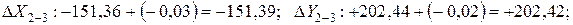
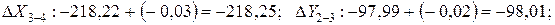
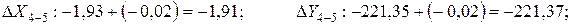
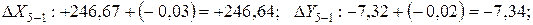
Контроль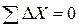 
; Контроль 
.
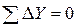Сумма исправленных приращений равна нулю, т.е. контроль выполняется.
