(задание 2.3)
Для закрепления умения применять логические операции полезно научиться выполнять упражнения двух типов:
- Дана некоторая область плоскости. Записать логическое выражение, принимающее значение «истина» тогда и только тогда, когда точка с координатами (x, y) принадлежит указанной области. Например, область ограничена прямыми
y = -x, x = 0, y = -1. Логическое выражение для ее записи:
if (y <= -x && x >= 0 && y > -1) cout << ”YES”; else cout << ”NO”; - По заданному выражению нарисовать область плоскости, в которой и только которой указанное выражение истинно. Например, нарисуйте область плоскости, в которой и только в которой истинно выражение:
x > y && x < 2 && y > -1;
x > y && x < 2 || y > -1;
x > y && (x < 2 || y > -1);
x > y || x < 2 && y > -2;
x > y || x < 2 || y > -1;
Такие задачи, в зависимости от того, какие логические операции используются при определении областей, можно классифицировать следующим образом:
· в выражении не используются логические операции. Например, точки первой и третьей четвертей, включая и оси координат, определяется с помощью выражения x*y >=0;
· используется только операция &&, если область состоит из одной части; например, точка внутри треугольника с вершинами (1, 1), (0, 0), (-1, 1) определяются так: y > abs(x) && y <=1;
· используется только операция ||, если область состоит из нескольких относительно несложных частей, для определения каждой из которых достаточно одного неравенства; например, область, состоящая из левой половины круга радиуса 2 с центром в начале координат, включая и полуокружность, и точек справа от оси OY определяется так: x > 0 || x*x + y*y <=4;
· используются как операция &&, так и операция ||, если область «склеена» из нескольких частей: каждая из них определяется с помощью нескольких неравенств, соединенных операцией &&; например, ту же левую половину круга радиуса 2, включая и его границы, и правую относительно оси OY часть полукольца, образованного окружностями радиусов 2 и 3 с центром в начале координат, можно определить так:
x <= 0 && x*x + y*y <=4 || x >=0 && x*x + y*y >= 4 && x*x + y*y <=9;
· используется операция отрицание (!), если легче определить область, которой точки не принадлежат, или некоторую часть уже определенной области надо «выбросить» из нее; например, так легче определить круг радиуса 5 с центром в начале координат, из которого выброшен треугольник с вершинами (1,1) (0, 0) и (-1, 1):
x*x + y*y <= 25 &&! (y >= abs(x) && y <=1).
Рассмотрим пример. Написать программу, проверяющую, попадает ли точка в заданную область. Результат вывести в виде текстового сообщения. Область можно описать как круг, пересекающийся с треугольником. Точка может попадать либо в круг, либо в треугольник, либо в их общую часть: {x2 + y2 <=1} или {х≤0 и y ≤ 0 и y ≥ -x-2}
 |
1
-2 1
-1
-2
int main()
{
double x, y;
cout << " input x, y" << endl;
cin >> x >> y; //с помощью условного оператора
if ( (x * x + y * y <= 1) || (x <= 0 && y <= 0 && y >= -x - 2) )
cout << "YES" << endl;
else cout << "NO" << endl;
_getch();
return 0;
}
Или
bool b =(x * x + y * y <= 1) || (x <= 0 && y <= 0 && y >= -x - 2);
if (b) cout << "YES" << endl;
else cout << "NO" << endl;
или с помощью условной тернарной операции:
cout <<
((( x * x + y * y <= 1 ) || ( x <= 0 && y <= 0 && y >= -x - 2 ))? "Yes": "No" );
Или
bool b =(x * x + y * y <= 1) || (x <= 0 && y <= 0 && y >= -x - 2);
cout << (b? "Yes": "No" );
-----------------------------------------------------------------------------------------
Вычислить результат логического выражения для переменных a, b, c. Обратить внимание на типы переменных:
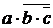
int main() //«прокрутить» операторы вручную и проверить результаты
{
Bool a, b, c, d;
a = true; b = true; c = false;
d = a && (!(b && (!c)));
cout << d << endl; // 0
_getch();
return 0;
}
-----------------------------------------------------------------------------------------
int main() //«прокрутить» операторы вручную и проверить результаты
{
Double a, b, c, d;
a = 1.2; b = -2.3; c = 0;
d = a && (!(b && (!c)));
cout << d << endl; // 0
_getch();
return 0;
}
-----------------------------------------------------------------------------------------
int main() //«прокрутить» операторы вручную и проверить результаты
{
Int a, b, c, d;
a = -1; b = -2; c = 1;
d = a && (!(b && (!c)));
cout << d << endl; // 1
_getch();
return 0;
}
-----------------------------------------------------------------------------------------
Вычислить результат логического выражения для логических переменных a, b, c:
a || b && c
int main() //«прокрутить» операторы вручную и проверить результаты
{
Bool a, b, c, d;
Int ia, ib, ic;
printf(" input a, b, c:\n");
printf("!=0 - true, ==0 - false:\n");
scanf_s("%i %i %i", &ia, &ib, &ic); //ввод переменых как целых
a = bool(ia); b=bool(ib); c = bool(ic); //приведение к логическому типу
d = a || b && c;
printf("d = %d \n ", d);
_getch();
return 0;
}
Результат:
1 1 1
d= 1
-----------------------------------------------------------------------------------------
Присвоить логической переменной b значение логического выражения, истинного при выполнении условия «целые n и k имеют одинаковую четность» и ложного в противном случае:
#include <stdio.h> // «прокрутить» операторы вручную и проверить результаты
#include <conio.h>
int main()
{
Int n, k;
Bool b;
printf("input n,k:\n");
scanf_s("%i %i", & n, & k);
b = (n % 2 == k % 2);
if (b) printf("odin");
else printf("razn");
printf("\nb==%d \n ", b);
_getch();
return 0;
}
Результат:
input n,k:
4 8
odin
b==1
-----------------------------------------------------------------------------------------






