5.21 На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна (l = 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, j = 20˚. Определить ширину a щели.
5.22 На дифракционную решетку, содержащую п= 100штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол D j = 16°. Определить длину волны l света, падающего на решетку.
5.23 На дифракционную решетку падает нормально монохроматический свет (l = 410 нм). Угол D j между направлениями на максимумы первого и второго порядков равен 2°21'. Определить число п штрихов на 1 мм дифракционной решетки.
5.24 Постоянная дифракционной решетки в п= 4раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол a между двумя первыми симметричными дифракционными максимумами.
5.25 Расстояние между штрихами дифракционной решетки d= 4 мкм. На решетку падает нормально свет с длиной волны l = 0,58 мкм. Максимум какого наибольшего порядка дает эта решетка?
5.26 Свет от монохроматического источника (l = 600 нм) падает нормально на диафрагму с диаметром отверстия d = 6 мм. За диафрагмой на расстоянии l = 3 м от нее находится экран. Какое число k зон Френеля укладывается в отверстие диафрагмы?
5.27 Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света (l = 600 нм). На расстоянии a = 0,5 l от источника помещена круглая непрозрачная преграда диаметром d = 1 см. Найти расстояние l, если преграда закрывает только центральную зону Френеля.
5.28 Между точечным источником света (l = 0,50 мкм) и экраном поместили диафрагму с круглым отверстием r = 1 мм. Расстояния от диафрагмы до источника и экрана равны соответственно R = 1 м и r 0 = 2 м. Как изменится освещенность экрана в точке, лежащей против центра отверстия, если диафрагму убрать?
5.29 Между точечным источником света (l = 0,50 мкм) и экраном поместили диафрагму с круглым отверстием r 1 = 0,75 мм. Расстояния от диафрагмы до источника и экрана равны соответственно R = r 0 = 0,75 м. Как изменится освещенность экрана в точке, лежащей против центра отверстия, если его радиус увеличить до r 2 = 0,87 мм?
5.30 На щель падает нормально параллельный пучок монохроматического света. Расположенная за щелью линза с фокусным расстоянием f = 2 м. проектирует на экран дифракционную картину в виде чередующихся светлых и темных полос. Ширина центральной светлой полосы b = 5 см. Как надо изменить ширину щели, чтобы центральная полоса занимала весь экран при любой ширине последнего?
5.31 Пластинку кварца толщиной d = 2 мм поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол j = 53°. Какой наименьшей толщины dmin следует взять пластинку, чтобы поле зрения поляриметра стало совершенно темным?
5.32 Параллельный пучок света переходит из глицерина в стекло так, что пучок, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определить угол g между падающим и преломленным пучками.
5.33 Кварцевую пластинку поместили между скрещенными николями. При какой наименьшей толщине dmin кварцевой пластины поле зрения между николями будет максимально просветлено? Постоянная вращения a кварца равна 27 град/мм.
5.34 При прохождении света через трубку длиной l 1 = 20 см, содержащую раствор сахара концентрацией С1= 10%, плоскость поляризации света повернулась на угол j 1 = 13,3°. В другом растворе сахара, налитом в трубку длиной l 2 = 15 см, плоскость поляризации повернулась на угол j 2 = 5,2 °. Определить концентрацию С2 второго раствора.
5.35 Пучок света последовательно проходит через два николя, плоскости пропускания которых образуют между собой угол j = 40°. Принимая, что коэффициент поглощения k каждого николя равен 0,15, найти, во сколько раз пучок света, выходящий из второго николя, ослаблен по сравнению с пучком, падающим на первый николь.
5.36 Угол падения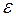 
луча на поверхность стекла равен 60°. При этом отраженный пучок света оказался максимально поляризованным. Определить угол 
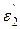преломления луча.
5.37 Угол a между плоскостями пропускания поляроидов равен 50°. Естественный свет, проходя через такую систему, ослабляется в п=8 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах.
5.38 Пучок света, идущий в стеклянном сосуде с глицерином, отражается от дна сосуда. При каком угле e падения отраженный пучок света максимально поляризован?
5.39 Пучок света переходит из жидкости в стекло. Угол падения 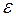пучка равен 60˚, угол преломления 
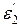= 50°. При каком угле падения 
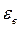пучок света, отраженный от границы раздела этих сред, будет максимально поляризован?
5.40 Пучок света падает на плоскопараллельную стеклянную пластину, нижняя поверхность которой находится в воде. При каком угле падения 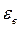свет, отраженный от границы – вода, будет максимально поляризован?
5.41 На сколько процентов уменьшится интенсивность света после прохождения через призму Николя, если потери света составляют 10%?
5.42 Естественный свет проходит через поляризатор и анализатор, поставленный так, что угол между их главными плоскостями равен j. Как поляризатор, так и анализатор поглощают и отражают 8% падающего на них света. Оказалось, что интенсивность луча, вышедшего из анализатора, равна 9% интенсивности естественного света, падающего на поляризатор. Найти угол j.
5.43 Луч света проходит через жидкость, налитую в стеклянный (n = 1,5) сосуд и отражается от дна. Отраженный луч полностью поляризован при падении его на дно сосуда под углом iб = 42°37'. Найти показатель преломления жидкости. Под каким углом i должен падать на дно сосуда луч света, идущий в этой жидкости, чтобы наступило полное внутреннее отражение?
5.44 Угол полной поляризации при отражении от кристалла каменной соли j = 57°05'. Определить скорость v распространения света в этом кристалле.
5.45 Найти угол j между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через поляризатор и анализатор, уменьшается в 4 раза.
5.46 Вычислить истинную температуру Т вольфрамовой раскаленной ленты, если радиационный периметр показывает температуру Трад= 2,5 кК. Принять, что поглощательная способность для вольфрама не зависит от частоты излучения и равна аi= 0,35.
5.47 Черное тело имеет температуру Т 1 = 500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в п= 5раз?
5.48 Температура абсолютно черного тела Т= 2 кК. Определить длину волны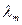 
, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости (rl,T)max для этой длины волны.
5.49 Определить температуру Т и энергетическую светимость Re абсолютно черного тела, если максимум энергии излучения приходится на длину волны lm = 600 нм.
5.50 Из смотрового окошечка печи излучается поток Фе = 4 кДж/мин. Определить температуру Т печи, если площадь окошечка S= 8 см 2.
5.51 Поток излучения абсолютно черного тела Фе = 10 кВт. Максимум энергии излучения приходится на длину волны lm = 0,8 мкм. Определить площадь излучающей поверхности.
5.52 Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (lm 1 = 780 нм) на фиолетовую (lm 2 = 390 нм)?
5.53 Определить поглощательную способность aТ серого тела, для которого температура, измеренная радиационным пирометром, Трад= 1,4 кК, тогда как истинная температура Т тела равна 3,2 кК.
5.54 Муфельная печь, потребляющая мощность, P= 1 кВт, имеет отверстие площадью S= 100 см 2. Определить долю h мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна 1 кК.
5.55 Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см 2× мин). Какова должна быть температура Т поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты aТ= 0,25?
5.56 Вычислить энергию, излучаемую за время t = 1 мин с площади S = 1 см 2 абсолютно черного тела, температура которого T = 1000 K.
5.57 Электрическая печь потребляет мощность P = 500 Вт. Температура ее внутренней поверхности при открытом небольшом отверстии диаметром d = 5 см равна 700° C. Какая часть потребляемой мощности рассеивается стенками?
5.58 Мощность излучения абсолютно черного тела P = 10 кВт. Найти площадь S излучающей поверхности тела, если максимум спектральной плотности его энергетической светимости приходится на длину волны l = 700 нм.
5.59 Абсолютно черное тело имеет температуру T 1 = 2900 K. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на D l = 9 мкм. До какой температуры T 2 охладилось тело?
5.60 Поверхность тела нагрета до температуры T = 1000 K. Затем одна половина этой поверхности нагревается на D T = 100 K, а другая охлаждается на D T = 100 K. Во сколько раз изменится энергетическая светимость R поверхности тела?
5.61 Красная граница фотоэффекта для цинка l 0 = 310 нм. Определить максимальную кинетическую энергию Ek,max фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны l = 200 нм.
5.62 На поверхность калия падает свет с длиной волны l = 150 нм. Определить максимальную кинетическую энергию Ek,max фотоэлектронов.
5.63 Фотон с энергией e = 10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс р, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.
5.64 На фотоэлемент с катодом из лития падает свет с длиной волны l = 200 нм. Найти наименьшее значение задерживающей разности потенциалов Umin, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.
5.65 Какова должна быть длина волны g -излучения, падающего на платиновую пластину, чтобы максимальная скорость фотоэлектронов была vmax = 3 Мм/с?
5.66 На металлическую пластину направлен пучок ультрафиолетового излучения (l = 0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов Umin= 0,96 В. Определить работу выхода А электронов из металла.
5.67 На поверхность металла падает монохроматический свет с длиной волны l = 0,1 мкм. Красная граница фотоэффекта l 0 = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
5.68 На металл падает рентгеновское излучение с длиной волны l = 1 нм. Пренебрегая работой выхода, определить максимальную скорость vmax фотоэлектронов.
5.69 На металлическую пластину направлен монохроматический пучок света с частотой n = 7,3×1014 Гц. Красная граница l 0фотоэффекта для данного материала равна 560 нм. Определить максимальную скорость vmax фотоэлектронов.
5.70 На цинковую пластину направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов U= 1,5 В. Определить длину волны l света, падающего на пластину.
5.71 На металлическую пластину падает монохроматический свет (l = 0, 413 мкм). Поток фотоэлектронов, вырываемых с поверхности металла, полностью задерживается, когда разность потенциалов тормозящего электрического поля достигает U= 1 В. Определить работу выхода в электронвольтах и красную границу фотоэффекта.
5.72 Фотоны с энергией e = 4,9 эВ вырывают электроны из металла с работой выхода A = 4,5 эВ. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона.
5.73 Найти постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой n 1 = 2,2×1015 Гц, полностью задерживаются разностью потенциалов U 1 = 6,6 В, а вырываемые светом с частотой n 2 = 4,6×1015 Гц - разностью потенциалов U 2 = 16,5 В.
5.74 Определить максимальную скорость vmax фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучение с длиной волны l 1 = 0,155 мкм; 2) g-излучением с длиной волны l 2 = 1 пм.
5.75 На пластину падает монохроматический свет (l = 0,42 мкм). Фототок прекращается при задерживающей разности потенциалов U 2 = 0,95 В. Определить работу выхода A электронов с поверхности пластины.
5.76 Фотон при эффекте Комптона на свободном электроне был рассеян на угол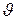 
=p/2. Определить импульс р (в МэВ/с), приобретенный электроном, если энергия фотона до рассеивания была e 1 = 1,02 МэВ.
5.77 Рентгеновское излучение (l = 1 нм) рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны lmax рентгеновского излучения в рассеянном пучке.
5.78 Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол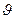 
= p/2? Энергия фотона до рассеяния e 1 = 0,51 МэВ.
5.79 Определить максимальное изменение длины волны (Dl) max при комптоновском рассеянии свет на свободных электронах и свободных протонах.
5.80 Фотон с длиной волны l 1 = 15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона l 2 = 16 пм. Определить угол 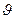рассеяния.
5.81 Фотон с энергией e 1 = 0,51 МэВ был рассеян при эффекте Комптона на свободном электроне на угол 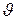= 180°. Определить кинетическую энергию Т электрона отдачи.
5.82 В результате эффекта Комптона фотон с энергией рассеян на свободных электронах на угол 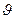= 150°. Определить энергию e 2 рассеянного фотона.
5.83 Определить угол 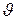, на который был рассеян квант с энергией e 1 = 1,53 МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи Т= 0,51 МэВ.
5.84 Фотон с энергией e 1 = 0,51 МэВ при рассеянии на свободном электроне потерял половину своей энергии. Определить угол рассеяния .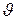
5.85 Определить импульс ре электрона отдачи, если фотон с энергией e 1 = 1,53 МэВ в результате рассеяния на свободном электроне потерял 1/3 своей энергии.
5.86 Определить энергетическую освещенность (облученность) Е е зеркальной поверхности, если давление р, производимое излучением равно 40 мкПа. Излучение падает нормально к поверхности.
5.87 Давление р света с длиной волны l = 40 нм, падающего нормально на черную поверхность, равно 2 нПа. Определить число N фотонов, падающих за время t = 10 c на площадь S = 1 мм 2этой поверхности.
5.88 Определить коэффициент отражения r поверхности, если при энергетической освещенности Е е=120 Вт/м 2давление р света на нее оказалось равным 0,5 мкПа.
5.89 На расстоянии r = 5 м от точечного монохроматического (l = 0,5 мкм) изотропного источника расположена площадка (S= 8 мм 2) перпендикулярно падающим пучкам. Определить число N фотонов, ежесекундно падающих на площадку. Мощность излучения Р= 100 Вт.
5.90 Точечный источник монохроматического (l = 1 нм) излучения находится в центре сферической зачерненной колбы радиусом R =10 см. Определить световое давление р, производимое на внутреннюю поверхность колбы, если мощность источника Р =1 кВт.
6.1 Невозбужденный атом водорода поглощает квант излучения с длиной волны l = 102,6 нм. Вычислить, пользуясь теорией Бора, радиус 
электронной орбиты возбужденного атома водорода.
6.2 Вычислить по теории Бора радиус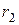 
второй стационарной орбиты и скорость v 2 электрона на этой орбите для атома водорода.
6.3 Вычислить по теории Бора период Т вращения электрона в атоме водорода, находящегося в возбужденном состоянии, определяемом главным квантовым числом 
.
6.4 Определить изменение энергии 
электрона в атоме водорода при излучении атомом фотона с частотой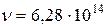 
Гц.
6.5 Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбужденное состояние атом излучил фотон с длиной волны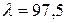 
нм?
6.6 На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны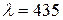 
нм?
6.7 В каких пределах D l должна лежать длина волн монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус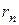 
орбиты электрона увеличился в 16 раз?
6.8 В однозарядном ионе лития электрон перешел с четвертого энергетического уровня на второй. Определить длину волны l излучения, испущенного ионом лития.
6.9 Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую Ek, потенциальную Ep и полную Е энергию электрона. Ответ выразить в электрон-вольтах.
6.10 Фотон выбивает из атома водорода, находящегося в основном состоянии, электрон с кинетической энергией Ek = 10 эВ. Определить энергию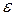 
фотона.
6.11 Определить квантовое число n возбужденного состояния атома водорода, если известно, что при переходе в основное состояние атом излучил: 1) фотон с длиной волны l = 97,25 нм; 2) два фотона, с l 1 = 656,3 нм и l 2 = 121,6 нм.
6.12 Определить скорость, которую приобрел покоившейся атом водорода в результате излучения фотона при переходе из первого возбужденного состояния в основное.
6.13 Вычислить радиус первой боровской орбиты однократно ионизированного атома гелия.
6.14 Максимальная длина волны спектральной водородной линии серии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридберга неизвестна, определить максимальную длину волны линии серии Бальмера.
6.15 Определить изменение орбитального механического момента электрона при переходе его из возбужденного состояния в основное с испусканием фотона длиной волны l = 1,02×10–7 м.
6.16 Вычислить наиболее вероятную дебройлевскую длину волны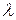 
молекул азота, содержащихся в воздухе при комнатной температуре.
6.17 Определить энергию D E, которую необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 
нм до 
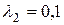нм.
6.18 На сколько по отношению к комнатной должна измениться температура идеального газа, чтобы дебройлевская, длина волны 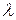его молекул уменьшилась на 20%?
6.19 Параллельный пучок моноэнергетических электронов падает нормально на диафрагму в виде узкой прямоугольной щели, ширина которой a = 0,06 мм. Определить скорость этих электронов, если известно, что на экране, отстоящем от щели на расстоянии 
мм, ширина центрального дифракционного максимума 
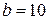мкм.
6.20 При каких значениях кинетической энергии Ek электрона ошибка в определении дебройлевской длины волны 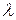по нерелятивистской формуле не превышает 10%?
6.21 Из катодной трубки на диафрагму с узкой прямоугольной щелью нормально к плоскости диафрагмы направлен поток моноэнергетических электронов. Определить анодное напряжение трубки, если известно, что на экране, отстоящем от щели на расстоянии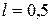 
м, ширина центрального дифракционного максимума 
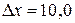мкм. Ширину b щели принять равной 0,10 мм.
6.22 Протон обладает кинетической энергией E = 1 кэВ. Определить дополнительную энергию D E которую необходимо ему сообщить для того, чтобы длина волны l де Бройля уменьшилась в три раза.
6.23 Определить длины волн де Бройля a-частйцы и протона, прошедших одинаковую ускоряющую разность потенциало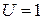в 
кВ.
6.24 Электрон обладает кинетической энергией E = 1,02 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия E электрона уменьшится вдвое?
6.25 Кинетическая энергия E электрона равна удвоенному значению его энергии покоя (
). Вычислить длину волны l де Бройля для такого электрона.
6.26 Вычислить длину волны де Бройля l для протона, движущегося со скоростью v = 0,6 c.
6.27 Найти кинетическую энергию, при которой дебройлевская длина волны электрона равна его комптоновской длине волны.
6.28 Определить длину волны де Бройля для атома водорода, движущегося при температуре T = 293 K с наиболее вероятной скоростью.
6.29 Определить длину волны де Бройля для нейтрона, движущегося при температуре T = 290 K со средней квадратичной скоростью.
6.30 Протон движется в однородном магнитном поле с индукцией B =15 мТл по окружности радиусом R = 1,4 м. Определить длину волн де Бройля для протона.
6.31 Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.
6.32 Используя соотношение неопределенностей, оценить наименьшие ошибки D v в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм.
6.33 Какова должна быть кинетическая энергия E протона в моноэнергетическом пучке, используемого для исследования структуры с линейными размерами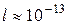 
см?
6.34 Используя соотношение неопределенностей, оценить ширину l одномерного потенциального ящика, в котором минимальная энергия электрона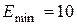 
эВ.
6.35 Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия a-частицы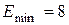 
МэВ.
6.36 Среднее время жизни атома в возбужденном состоянии составляет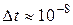 
с. При переходе атома в нормальное состояние испускается фотон, средняя длина волны < l > которого равна 600 нм. Оценить ширину D l, излучаемой спектральной линии, если не происходит ее уширения за счет других процессов.
