ѕусть скал€рное поле  имеет в некоторой точке ћ0 значение U0, и пусть при перемещении
имеет в некоторой точке ћ0 значение U0, и пусть при перемещении  по направлению вектора
по направлению вектора  мы приходим из точки ћ0 в точку ћ, где скал€рное поле имеет значение Us. ѕриращение U при этом перемещении равно
мы приходим из точки ћ0 в точку ћ, где скал€рное поле имеет значение Us. ѕриращение U при этом перемещении равно  . ѕредел отношени€ этого приращени€ dU к численной величине перемещени€ ds называетс€ производной скал€ра U в точке ћ0 по направлению
. ѕредел отношени€ этого приращени€ dU к численной величине перемещени€ ds называетс€ производной скал€ра U в точке ћ0 по направлению  :
:

«начение этой производной существенно зависит от выбора направлени€  и ее ни в коем случае нельз€ смешивать с обыкновенной частной производной по скал€рному параметру s. „тобы подчеркнуть это обсто€тельство, часто такую производную обозначают:
и ее ни в коем случае нельз€ смешивать с обыкновенной частной производной по скал€рному параметру s. „тобы подчеркнуть это обсто€тельство, часто такую производную обозначают: 
12. √радиент.
√радиентом пол€  называетс€ вектор, определ€емый в каждой точке пол€ соотношением:
называетс€ вектор, определ€емый в каждой точке пол€ соотношением: 
“огда  , где
, где  - единичный вектор в направлении
- единичный вектор в направлении  .
.
„асто вектор grad U обозначают также  или
или  , где
, где  ("набла") обозначает символический вектор, называемый оператором √амильтона или набла-оператором:
("набла") обозначает символический вектор, называемый оператором √амильтона или набла-оператором:
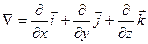
13. ѕоток пол€ через поверхность.
–азобьем данную поверхность S на n элементарных площадок размером  . ¬нутри каждой площадки выберем точку
. ¬нутри каждой площадки выберем точку  - и в этой точке построим нормальный к поверхности единичный вектор
- и в этой точке построим нормальный к поверхности единичный вектор  и вектор
и вектор  направление которого
направление которого  а модуль
а модуль  . “огда мы определ€ем:
. “огда мы определ€ем:
1) ѕоток скал€рного пол€: 
2) —кал€рный поток векторного пол€: 
3) ¬екторный поток векторного пол€: 
14 .ѕроизводна€ по объему.
ѕод производными по объему скал€рного или векторного полей в точке ћ понимают величины трех типов, которые получают следующим образом.
(1) “очка ћ окружаетс€ замкнутой поверхностью S, котора€ охватывает область с объемом V. (2) ¬ычисл€етс€ интеграл  по поверхности S:
по поверхности S:

 , или
, или  , или
, или  . (3) ќпредел€етс€ предел
. (3) ќпредел€етс€ предел 
отношени€ этого интеграла к объему V, когда S ст€гиваетс€ в точку ћ, так что V стремитс€ к нулю.
15. ƒивергенци€ векторного пол€.
ƒивергенцией (обозначаетс€  ) векторного пол€
) векторного пол€  называют следующую производную по объему пол€ в точке ћ:
называют следующую производную по объему пол€ в точке ћ:

¬еличина  есть скал€рный поток векторного пол€ через замкнутую поверхность S, котора€ окружает точку ћ и охватывает область G с объемом V.
есть скал€рный поток векторного пол€ через замкнутую поверхность S, котора€ окружает точку ћ и охватывает область G с объемом V.
ƒивергенци€  есть мера источников пол€
есть мера источников пол€  . ≈сли в области G
. ≈сли в области G  , то векторное поле
, то векторное поле  называетс€ свободным от источников. “е точки пол€, в которых
называетс€ свободным от источников. “е точки пол€, в которых  прин€то называть источниками пол€, а те, в которых
прин€то называть источниками пол€, а те, в которых  Ч стоками пол€. 16. ‘ормула √аусса-ќстроградского.
Ч стоками пол€. 16. ‘ормула √аусса-ќстроградского.
ƒл€ пространственной области G, ограниченной замкнутой поверхностью S:

17. ќператор Ћапласа.
ѕусть U(M) Ч скал€рное поле, тогда оператор Ћапласа  определ€етс€ следующим образом:
определ€етс€ следующим образом:
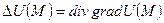
или в декартовых координатах:

ќператор Ћапласа векторного пол€: 
18. –отор векторного пол€.
–отором (вихрем) векторного пол€  называют следующую производную по объему пол€ в точке ћ:
называют следующую производную по объему пол€ в точке ћ:

ќбозначаетс€: 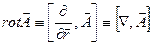
19. “еорема —токса.
÷иркул€ци€ векторного пол€  по замкнутой кривой L равна потоку ротора этого пол€ черезповерхность S, опирающуюс€ на кривую L:
по замкнутой кривой L равна потоку ротора этого пол€ черезповерхность S, опирающуюс€ на кривую L:


ѕримечание.
¬ этом приложении приведены определени€ некоторых математических пон€тий, часто используемых в курсе физики. ћатериал носит справочный характер, поскольку предполагаетс€, что данные пон€ти€ известны читателю.
|
|
|

√–≈„≈— »… јЋ‘ј¬»“
| ѕрописные | —трочные | Ќазвание | ѕрописные | —трочные | Ќазвание | ѕрописные | —трочные | Ќазвание |
| Α | α | јльфа | Ι | ι | …ота | Ρ | ρ | –о |
| Β | β | Ѕэта | Κ | Κ | аппа | Σ | σ,ς | —игма |
| Γ | γ | √амма | Λ | Λ | Ћ€мбда | Τ | τ | “ау |
| Δ | δ | ƒэльта | Μ | Μ | ћю | Υ | Υ | »-псилон |
| Ε | ε | Ё-псилон | Ν | Ν | Ќю | Φ | Φ | ‘и |
| Ζ | ζ | ƒзэта | Ξ | ξ | си | Χ | Χ | ’и |
| Η | η | Ёта | Ο | Ο | ќ-микрон | Ψ | Ψ | ѕси |
| Θ | θ | “эта | Π | Π | ѕи | Ω | Ω | ќ-мега |






