Продифференцируем по времени уравнение гармонических ко-лебаний
| x = A cos(ω t +ϕ0). | (5.3.1) | ||||||||
| и получим выражение для скорости | |||||||||
| υ= dx | = | d | (A cos(ω t +ϕ 0))= − A ω sin (ω t +ϕ 0) = | ||||||
| dt | |||||||||
| dt | . | (5.3.2) | |||||||
| π | |||||||||
| +ϕ 0 | + | ||||||||
| = A ω cos ω t | |||||||||
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2. Амплитуда скорости равна А ω.
Продифференцировав уравнение (2) еще раз по времени, полу-чим выражение для ускорения
| а = d υ | = | d | (− A ω sin (ω t +ϕ 0))= − A ω2 сos (ω t +ϕ 0) = | |
| dt | ||||
| dt | . (5.3.3) | |||
| = A ω2 cos (ω t +ϕ 0 + π) |
| Рис. 5.3.1 |
x
+ A 0
− A
υ x
+ω A
−ω A
α x
+ω2 A 0
−ω2 A
Как следует из уравнения (5.3.3), ус-корение и смещение находятся в противо-фазе. Это означает, что в тот момент вре-
t мени, когда смещение достигает наиболь-шего, положительного значения, ускорение достигает наибольшего по величине отри-цательного значения, и наоборот. Ампли-
туда ускорения равна А ω2 (рис. 5.3.1).
t Из выражения (5.3.3) следует диффе-ренциальное уравнение гармонических ко-лебаний
| d 2 x | |||
| t | dt 2 | +ω x = 0, | (5.3.4) |
где x = A cos(ω t +α).
Результирующая сила, действующая
на материальную точку массой m, определяется с помощью второго закона Ньютона. Проекция этой силы
| F = ma = − mA ω2cos(ω t +ϕ | ) = − m ω2 x. | (5.3.5) |
Эта сила пропорциональна смещению точки из положения рав-новесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой. Таким образом, гармонические ко-лебания происходят под действием силы F, пропорциональной сме-щению x и направленной к положению равновесия,
| F =− kx, | (5.3.6) |
где k = m ω2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая за-висимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости
(5.3.6) называются квазиупругими силами.
Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором. Ее динами-ческое поведение описывается дифференциальным уравнением
| линейного ос- |
| F = ma = − m ω2 x ⇒ | d 2 x +ω2 x = 0 | , | (5.3.7) | ||
| dt 2 | |||||
ω0 − собственная частота осциллятора.
Решение этого уравнения дает закон движения циллятора x = A cos (ω t +ϕ0).
| 5.4. Энергия гармонических коле- | |||||||
| баний | a) | П = mgl | |||||
| В процессе колебаний происходит | |||||||
| t = 0 | К = 0 | ||||||
| превращение кинетической энергии в по- | |||||||
| тенциальную | энергию и | обратно (рис. | h | ||||
| 5.4.1). В момент наибольшего отклонения | |||||||
| от положения равновесия полная энергия | |||||||
| состоит только из потенциальной энер- | б) | П = 0 | |||||
| гии, которая достигает своего наиболь- | m υ2 | ||||||
| шего значения. Далее при движении к | t = T /4 | К = | |||||
| положению | равновесия | потенциальная | |||||
| энергия уменьшается, при этом кинети- | υ | ||||||
| ческая энергия возрастает. При прохож- | |||||||
| дении через положение равновесия пол- | |||||||
| ная энергия состоит лишь из кинетиче- | в) | ||||||
| ской энергии, которая в этот момент дос- | t = T /2 | П = mgl | |||||
| тигает своего наибольшего значения. Да- | К = 0 | ||||||
| лее при движении к точке наибольшего | h | ||||||
| отклонения происходит уменьшение ки- | |||||||
| нетической и увеличение потенциальной | Рис. 5.4.1 |
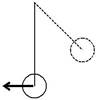
энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана ну-лю. И т. д.
Потенциальная энергия тела, совершающего гармонические ко-лебания равна
| П = | kx 2 | = | 1 | = | 1 | (ω t +ϕ) = | 1 | (ω t +ϕ). (5.4.1) | ||||||||
| m ω x | kA cos | m ω | A cos | |||||||||||||
Кинетическая энергия тела, совершающего гармонические ко-лебания равна
| K= m υ2 | = | 1 m ω2 A 2sin2 | (ω t +ϕ 0) = | 1 kA 2sin2 | (ω t +ϕ0). (5.4.2) |
Таким образом, полная энергия гармонического колебания, со-стоящая из суммы кинетической и потенциальной энергий, определя-ется следующим образом
| E =K+ | П = | 1 kA 2sin2(ω t +ϕ0)+ | |||||
| . | (5.4.3) | ||||||
| + | 1 kA 2cos2 | (ω t +ϕ 0) = | 1 kA 2 | = | 1 m ω2 A 2 | ||
Следовательно, полная энергия гармонического колебания
| kx 2 | m υ2 | 1 2 | = const. | (5.4.4) | ||||
| E = | 2 + | = | 2 m ω A |
оказывается постоянной в случае гармонических колебаний.
Найдем среднее значение потенциальной энергии за период ко-лебания
| П = | kA | cos | ϕ = | kA | 2π | = | |||||||||||||||
| ∫ cos | ϕ d ϕ | ||||||||||||||||||||
| 2π 0 | . | (5.4.5) | |||||||||||||||||||
| 2π 1 | + cos 2ϕ | ||||||||||||||||||||
| = | kA | = | kA | ||||||||||||||||||
| 2 π | ∫ | d ϕ | |||||||||||||||||||
| 0 |
Аналогично получается для среднего значение кинетической энергии
| K = | 1 kA 2 | sin2 ϕ = | 1 kA 2. | (5.4.6) |
Таким образом, и потенциальная, и кинетическая энергии изме-няются относительно своих средних значений по гармоническому за-
кону с частотой 2ω и амплитудой 1 4 kA 2.
5.5. Пружинный,
