Обуславливается передвижением ионов самого диэлектрика, так и ионов случайных примесей, а у некоторых материалов может быть вызвана наличием свободных электронов.
Удельная проводимость при некоторой температуре Т выражается по формуле, что и для жидких диэлектриков: 
. Полагая, что при ионной проводимости число диссоциированных ионов и их подвижность, находящихся в экспонициальной зависимости от Т: 
. 
и 
соответствуют значению Т= ¥, W0 - энергия освобождения ионов, Wn – энергия перемещения иона, определяющая переход его из одного неравновесного состояние в другое.
Используя все эти формулы и объединяя постоянные и в один коэффициент А, получим: 
. В виду того, что W0>Wn удельная проводимость при изменении Т определяется главным образом изменением концентрации носителей.
Коэффициент b учитывает увеличение передвижением свободных ионов и твердых тел при увеличении Т.
Если в диэлектрике ток обусловлен передвижением ионов, то проводимость можно записать: 
. Заменяя g на 
, получим: 
. При использовании этого выражения температурный коэффициент удельного сопротивления можно записать: 
Диэлектрические потери.
Диэлектрическими потерями называют мощность, которая рассеивается в диэлектрике при воздействии на него электрического поля и вызывающее нагрев диэлектрика.
Потери в диэлектриках обнаруживаются как при постоянном напряжении, так и при переменном. Поскольку в диэлектрике наблюдается сквозной ток, обусловленный проводимостью. При постоянном напряжении потери характеризуются значениями удельной объемной и удельной поверхностной сопротивлениями. При переменном напряжении нужно использовать другую характеристику, т.к. кроме сквозного тока возникают другие причины, которые вызывают потри. Диэлектрические потери можно характеризовать рассеиваемой мощностью в единице объема – удельной потери.
Чаще для оценки способности диэлектрика рассеивать мощность в электрическом поле пользуются углом диэлектрических потерь. Углом диэлектрических потерь называется угол, дополняющий до 900 угол фазового сдвига j между током и напряжением в емкостной цепи.
Для идеального диэлектрика вектор тока будет опережать вектор напряжения на 900, при этом угол диэлектрических потерь равен нулю.
Тангенс угла диэлектрических потерь непосредственно входит в формулу для величины рассеиваемой мощности и пользуются 
Рассмотрим схему эквивалентную конденсаторам диэлектрика, обладающего потерями. Эта схема должна быть выбрана так, чтобы активная мощность, расходуемая в схеме была равна мощности, рассеиваемой в диэлектрике, а ток опережал напряжение на тот же угол, что и рассматривался в конденсаторе. Заменим конденсатор с потерями идеальным конденсатором с последовательно включенным активным сопротивлением или идеальным конденсатором с шунтированным идеальным сопротивлением:
Из теории переменных токов известно, что активная мощность равна: 
. Для последовательной схемы: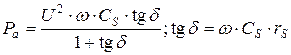 
. Для параллельной схемы: 
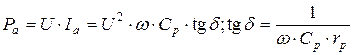. Приравнивая 1-ю формулу к 3-й, 2-ю к 4-й, находим соотношения между Cp, CS, rp, rS: 
.
Для высококачественных диэлектриков можно пренебречь значениями 
и считать Cp=CS, rp=rS, следовательно, выражения мощности будут равны для обеих схем: 
, w - угловая частота, Ра – активная мощность, U – напряжение, С – емкость.
Выражение для удельной электрической потери: 
, Е – напряженность, р – удельные потери.
