1. ѕринцип относительности √алиле€ (в классической механике) утверждает:
а) ЂЌикакие опыты, проводимые в любых системах отсчета с механическими приборами, не позвол€ют установить, покоитс€ система отсчета или движетс€ равномерно и пр€молинейно по отношению к другой отсчетаї;
б) ЂЌикакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позвол€ют установить, покоитс€ система отсчета или движетс€ равномерно и пр€молинейно по отношению к другой произвольной системе отсчетаї;
в) ЂЌикакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позвол€ют установить, покоитс€ система отсчета или движетс€ равномерно и пр€молинейно по отношению к другой инерциальной системе отсчетаї.
ѕримечание. ѕредполагаетс€, что врем€ не зависит от относительного движени€ систем отсчета.
2. ѕреобразовани€ √алиле€ определ€ют положение произвольной материальной точки в двух инерциальных системах отсчета, одна из которых движетс€ со скоростью  относительно другой при условии:
относительно другой при условии:
а) если направление скорости  не совпадает с направлением радиус-вектора
не совпадает с направлением радиус-вектора  , определ€ющим положение начала координат подвижной системы отсчЄта ' в неподвижной системе координат ;
, определ€ющим положение начала координат подвижной системы отсчЄта ' в неподвижной системе координат ;
б) если направление скорости  совпадает с направлением радиус-вектора
совпадает с направлением радиус-вектора  , определ€ющим положение начала координат подвижной системы отсчЄта ' в неподвижной системе координат ;
, определ€ющим положение начала координат подвижной системы отсчЄта ' в неподвижной системе координат ;
в) если направление скорости  совпадает с направлением радиус-вектора
совпадает с направлением радиус-вектора  , определ€ющим положение начала координат подвижной системы отсчЄта '.
, определ€ющим положение начала координат подвижной системы отсчЄта '.
3. ¬ векторной форме преобразовани€ √алиле€ можно представить так:
а)  , где
, где  и
и  Ц радиус-векторы, определ€ющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени;
Ц радиус-векторы, определ€ющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени;  Ц радиус-вектор, определ€ющий положение начала подвижной системы координат ' в неподвижной системе координат ;
Ц радиус-вектор, определ€ющий положение начала подвижной системы координат ' в неподвижной системе координат ;
б)  , где
, где  и
и  Ц радиус-векторы, определ€ющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени;
Ц радиус-векторы, определ€ющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени;  Ц скорость движени€ подвижной системы координат;
Ц скорость движени€ подвижной системы координат;
в)  , где
, где  и
и  Ц радиус-векторы, определ€ющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени;
Ц радиус-векторы, определ€ющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени;  Ц скорость движени€ подвижной системы координат.
Ц скорость движени€ подвижной системы координат.
4. »спользу€ преобразовани€ √алиле€ в проекци€х на оси координат в произвольный момент времени t, координату x выбранной точки в неподвижной системе отсчета можно определить так:
а)  ;
;
б)  ;
;
в)  .
.
5. »спользу€ преобразовани€ √алиле€ в проекци€х на оси координат в произвольный момент времени t, координату y выбранной точки в неподвижной системе отсчета можно определить так:
а)  ;
;
б)  ;
;
в)  .
.
6. »спользу€ преобразовани€ √алиле€ в проекци€х на оси координат в произвольный момент времени t, координату z выбранной точки в неподвижной системе отсчета можно определить так:
а) 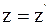 ;
;
б)  ;
;
в) 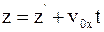 .
.
7. ѕреобразовани€ √алиле€ справедливы в том случае, когда врем€ в подвижной инерциальной системе отсчЄта и неподвижной инерциальной системе отсчЄта:
|
|
|
а)  ;
;
б)  ;
;
в) 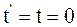 .
.
8. »спользу€ преобразовани€ √алиле€ в проекци€х на оси координат в произвольный момент времени t, координату x' выбранной точки в подвижной системе отсчета ' можно определить так:
а)  ;
;
б)  ;
;
в)  .
.
9. »спользу€ преобразовани€ √алиле€ в проекци€х на оси координат в произвольный момент времени t, координату y' выбранной точки в подвижной системе отсчета ' можно определить так:
а)  ;
;
б)  ;
;
в)  .
.
10. »спользу€ преобразовани€ √алиле€ в проекци€х на оси координат в произвольный момент времени t, координату z' выбранной точки в подвижной системе отсчета ' можно определить так:
а)  ;
;
б)  ;
;
в)  .
.
11. овариантные, или инвариантные, уравнени€ Ц это уравнени€, обе части которых при переходе от одной системы координат к другой преобразуютс€:
а) одинаково и сохран€ют свой вид во всех инерциальных системах отсчета;
б) неодинаково и несохран€ют свой вид во всех инерциальных системах отсчета;
в) одинаково, но несохран€ют свой вид во всех инерциальных системах отсчета.
12. «акон сложени€ скоростей в классической механике отображаетс€ соотношением:
а) 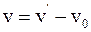 ;
;
б)  ;
;
в)  .
.
13. “еори€ относительности Ц это физическа€ теори€, рассматривающа€ пространственно-временные закономерности, справедливые:
а) только дл€ механических процессов;
б) только дл€ оптических процессов;
в) дл€ любых физических процессов.
14. »нвариантность (симметри€) законов физики Ц это неизменность законов физики, устанавливающих соотношение между величинами, характеризующими физическую систему или определ€ющими изменение этих величин:
а) в пространстве при преобразовани€х;
б) со временем при преобразовани€х;
в) в пространстве и со временем при преобразовани€х.
15. ќтносительное рассто€ние между выбранными точками пространства в подвижных системах отсчета определ€етс€ соотношением:
а)  ;
;
б)  ;
;
в) 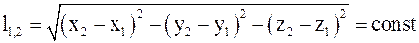 .
.
16. ќтносительное рассто€ние между выбранными точками пространства в неподвижных системах отсчета определ€етс€ соотношением:
а)  ;
;
б)  ;
;
в) 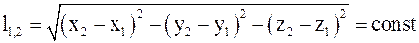 .
.
17. »нварианты преобразований Ц это инвариантные величины:
а) рассто€ни€ между телами (точками);
б) промежутки времени между событи€ми;
в) относительные скорости и ускорени€ тел.
18. ѕервый постулат специальной теории относительности (принцип относительности) утверждает:
а) Ђћеханические и тепловые физические опыты, производимые внутри инерциальной системы отсчета, позвол€ют установить, находитс€ ли она в равномерном абсолютном и пр€молинейном движении или нетї;
б) ЂЌикакие электромагнитные и оптические опыты, производимые внутри инерциальной системы отсчета, не позвол€ют установить, находитс€ ли она в равномерном абсолютном и пр€молинейном движении или нетї;
в) ЂЌикакие физические опыты (механические, оптические, тепловые, электромагнитные и т.д.), производимые внутри инерциальной системы отсчета, не позвол€ют установить, находитс€ ли она в равномерном абсолютном и пр€молинейном движении или нетї.
19. ¬торой постулат специальной теории относительности утверждает:
а) Ђ—корость света в вакууме одинакова во всех направлени€х и не зависит от движени€ источника светаї;
б) Ђ—корость света в вакууме одинакова во всех направлени€х и зависит от движени€ источника светаї;
в) Ђ—корость света в вакууме не зависит от движени€ источника светаї.
20. “ретий постулат специальной теории относительности утверждает:
|
|
|
а) Ђ—обыти€, одновременные в одной системе отсчета, €вл€ютс€ одновременными в другой системе отсчетаї;
б) Ђ—обыти€, одновременные в одной системе отсчета, не €вл€ютс€ одновременными в другой системе отсчетаї;
в) Ђќдновременность событий €вл€етс€ пон€тием относительнымї.
21. ‘ормула преобразовани€ координаты x в неподвижной системе координат, согласно преобразовани€м Ћоренца, имеет вид:
а)  ;
;
б)  ;
;
в)  .
.
22. ‘ормула преобразовани€ координаты x' в подвижной системе координат, согласно преобразовани€м Ћоренца, имеет вид:
а)  ;
;
б)  ;
;
в)  .
.
23. ‘ормула преобразовани€ времени в неподвижной системе координат, согласно преобразовани€м Ћоренца, имеет вид:
а)  ;
;
б) 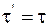 ;
;
в)  .
.
24. ‘ормула преобразовани€ времени в подвижной системе координат, согласно преобразовани€м Ћоренца, имеет вид:
а)  ;
;
б) 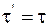 ;
;
в)  .
.
25. ≈сли частица движетс€ в неподвижной системе отсчЄта вдоль оси x со скоростью v, то в момент времени t в подвижной системе отсчЄта, движущейс€ относительно неподвижной со скоростью u, скорость частицы v', согласно преобразовани€м Ћоренца, определ€етс€ соотношением:
а)  ;
;
б)  ;
;
в)  .
.
26. „асы, наход€щиес€ в неподвижной системе отсчЄта в точке х = 0, показывают врем€ t. ¬ подвижной системе отсчЄта ' часы, пространственно совпадающие с часами в неподвижной системе отсчЄта в этот момент времени, показывают врем€:
а)  ;
;
б)  ;
;
в)  .
.
27. —оотношение, отображающее показани€ часами, наход€щимис€ в неподвижной системе отсчЄта в точке х = 0, и часами, наход€щимис€ в подвижной системе отсчЄта ', пространственно совпадающими с часами в неподвижной системе отсчЄта , имеет вид:
а)  ;
;
б)  ;
;
в)  .
.
28. ƒлина стержн€ в подвижной инерциальной системе отсчЄта (в направлении еЄ скорости движени€ v) отображаетс€ соотношением:
а)  ;
;
б)  ;
;
в)  .
.
29. –азмеры всех тел, поко€щихс€ в неподвижной инерциальной системе отсчЄта, при измерении в подвижной инерциальной системе отсчЄта (в направлении еЄ скорости движени€ v) оказываютс€:
а) равными  ;
;
б) меньше в  ;
;
в) больше в  .
.
30. ѕродольный диаметр сферы, движущейс€ со скоростью v относительно неподвижной инерциальной системы отсчЄта, при измерении в подвижной инерциальной системе отсчЄта будет:
а) равен поперечному диаметру;
б) больше в  раз поперечного диаметра;
раз поперечного диаметра;
в) меньше в  раз поперечного диаметра.
раз поперечного диаметра.
31. осмический корабль с двум€ космонавтами летит со скоростью v = 0,8c (с Ц скорость распространени€ света в вакууме). ќдин из космонавтов медленно поворачивает метровый стержень из положени€ 1, параллельного направлению движени€, в положение 2, перпендикул€рное этому направлению. “огда длина стержн€ с точки зрени€ другого космонавта:
а) изменитс€ от 1,0 м в положении 1 до 1,67 м в положении 2;
б) равна 1,0 м при любой его ориентации;
в) изменитс€ от 1,0 м в положении 1 до 0,6 м в положении 2;
г) изменитс€ от 0,6 м в положении 1 до 1,0 м в положении 2.
32. »мпульс (вектор энергии Ц импульса) материальной точки в специальной теории относительности определ€етс€ соотношением:
а)  ;
;
б) 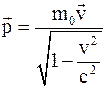 ;
;
в) 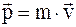 .
.
33. ”равнение движени€ материальной точки в специальной теории относительности можно записать так:
а) 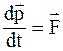 ;
;
б)  ;
;
в)  .
.
34. инетическа€ энерги€ тела в специальной теории относительности определ€етс€ соотношением:
а)  ;
;
б)  ;
;
в)  .
.
35. ћежду массой вс€кого физического объекта и присущей ему (во взаимосв€зи с окружающей средой) полной энергией E имеет место соотношение:
а)  ;
;
б)  ;
;
в)  .
.
36. ¬с€кое изменение энергии тела на величину D≈ влечет за собой изменение массы тела на Dm, причем:
а)  ;
;
б)  ;
;
в)  .
.
37. «акон взаимной св€зи энергии и массы утверждает: Ђ¬с€ка€ матери€ (вещество в обычном смысле или излучение), обладающа€ энергией ≈, обладает тем самым и массой m, равной:
а)  ї;
ї;
б)  ї;
ї;
в) 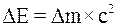 ї.
ї.






