Активное и внутреннее индуктивное сопротивление проводников можно определить с помощью теоремы Умова – Пойнтинга в комплексной форме.
Перед тем, как записать теорему Умова – Пойнтинга 4.8) в комплексной форме, рассмотрим вопрос о полной мощности в цепи синусоидального тока. Полная мощность
Здесь 
- сопряженное значение комплекса тока 
.
Пусть цепь синусоидального тока содержит последовательно соединенные активные сопротивления R, индуктивность L и емкость С.
Тогда реактивная мощность
Здесь 
и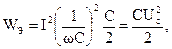 
где Uc – напряжение на конденсаторе.
Таким образом, реактивная мощность Q равна разности между магнитной WМ и электрической WЭ энергиями цепи, умноженной на 2w.
Введем также в рассмотрение комплексный вектор Пойнтинга 
 |
Последнее выражение отличается от мгновенного значения вектора Пойнтинга тем, что здесь комплексная величина вектора напряженности
электрического поля умножается на сопряженное значение 
вектора напряженности магнитного поля.
С учетом этого, теорему Умова – Пойнтинга (4.8) можно переписать в следующем виде:
Первое слагаемое правой части данного выражения представляет собой активную мощность, второе – реактивную. Таким образом, теорему Умова – Пойнтинга можно записать еще следующим образом:
В таком виде ее и используют для определения активного и внутреннего индуктивного сопротивления проводников на переменном токе. С этой целью подсчитывают поток вектора Пойнтинга через боковую поверхность проводника на необходимой длине (например, 1 м) и делят его на квадрат тока, протекающего по проводнику, в результате чего и получают комплексное сопротивление проводника на этой длине
В качестве примера определим активное и внутреннее индуктивное сопротивление цилиндрического провода (см. рис. 5.11) на длине l:
(5.14)
Здесь d – радиус (новое обозначение введено, чтобы отличать от сопротивления) проводника; 
и 
- комплексная амплитуда напряженности электрического поля и сопряженное значение комплексной амплитуды напряженности магнитного поля на поверхности проводника.
Используя формулу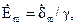 
а также выражения (5.11), (5.12) и (5.13), преобразуем уравнение (5.14) к следующему виду:
Если рассчитать сопротивление данного провода на длине l постоянному току, то оно будет равно 1.273×10-3l. Таким образом,
Отсюда видно, что активное сопротивление провода почти в четыре раза превышает сопротивление провода постоянному току.
Отметим, что если поле обладает цилиндрической симметрией, как в случае прямолинейного одиночного провода (обратный провод находится достаточно далеко) или в случае прямолинейного цилиндрического кабеля, то выражение для определения активного и внутреннего индуктивного сопротивления провода можно получить и иным путем
. (5.15)
Здесь 
- комплексное значение падения напряжения на длине l провода.
Формула (5.15) просто получается и из выражения (5.14), если в нем заменить квадрат тока его значением, определенным с помощью закона полного тока
