КОНСТРУИРОВАНИЕ И РАСЧЁТ ОСНОВНОЙ НЕСУЩЕЙ КОНСТРУКЦИИ ПОКРЫТИЯ
Ограждающие конструкции покрытия и стен выполняются из плит с одной верхней обшивкой.
Ширину плиты принимаем по максимальной ширине асбестоцементного листа – 1200 мм, толщина обшивки – 8мм, длина – 3900мм (ГОСТ 18124-95), (таблица 2.14,стр. 251 [3]).
Каркас подбирается следующим способом:
- расстояние между продольными ребрами: a<500мм, кратно размерам штучного материала;
- расстояние между поперечными ребрами: менее 1,5м или ребра устанавливаются в местах стыка обшивки.
Толщина плиты 
.
Рисунок 1. Основные размеры клеефанерной плиты с одной верхней обшивкой из асбестоцементных листов.
Согласно сортаменту принимаем сечение ребра равное 100×32.
Таким образом полную высоту сечения плиты равна:100+8=108 мм.
Шаг продольных рёбер 350 мм, шаг поперечных рёбер 1250 мм.
ОПРЕДЕЛЕНИЕ НАГРУЗОК НА ПЛИТУ
На плиту покрытия действуют нагрузки:
- постоянные: вес кровли, собственный вес плиты;
- временные: снеговая.
Район строительства – г. Брест (I Б район по весу снегового покрова) (с.233 [3]).
Таблица 1. - Нагрузки, действующие на 1 м2 площади покрытия.
| Наименование нагрузок | Нормативная нагрузка кН/м2 | Коэффициент надёжности по нагрузке | Расчётная нагрузка кН/м2 |
| Постоянная: | |||
| - кровля «Стеклоизол» 2 слоя (расход 4,5 кг на м2 (c.227,т.1.1[3])) | 0,09 | 1,3 | 0,117 |
- каркас деревянный  кг/м3 (таблица 2.3, с.240 [3])
| 0,1041 | 1,1 | 0,1145 |
- утеплитель: плиты минераловатные мягкие  (т.1.2, с.228 [3])
| 0,28 | 1,2 | 0,336 |
- пароизоляция 
| 0,003 | 1,2 | 0,0036 |
- обшивка – листы плоские асбестоцементные ЛП-НП  кг/м3  (таблица 2.15, с.251 [3])
| 0,128 | 1,2 | 0,1536 |
| Всего | 0,6051 | - | 0,7247 |
| Временная: | |||
- снеговая
S0=0,8 кПа (таблица 1.8, с.232 [3]), 
| 1,00 | 1,6 | 1,6 |
| Итого | 1,6051 | - | 2,3247 |
Нормативная постоянная нагрузка на 1 м2 от:
- каркаса деревянного:
V = (0,01248∙4+0,0010176∙12) = 0,0621312 м3;
gk3=m∙g/A=800∙0,0621312∙9,8/3,9∙1,2=0,1041 кН/м2
- обшивки:
ρ× δ = 1600∙0,008∙10-2=0,128 кН/м2.
Временная нагрузка на 1 м2 от веса снегового покрова.
Временная нагрузка на 1 м2 от веса снегового покрова: qs.k = Sg × μ
где Sg – расчетное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли (табл. 1.8, стр.232, [3]), Sg=0,8 кПа;
μ – коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие (таблица 1.9, стр.234, [3]), т.к. 
μ=1
Принимаем вариант нагружения №2 (номер схемы 1, таблица 1.9, [3])
Наиболее нагруженными являются два промежуточных ребра, так как нагрузка, воспринимаемая ребром, собирается с двух полупролетов справа и слева от ребра.
Линейно распределенная нагрузка на расчетное среднее ребро равна (определяемая с учетом шага продольных ребер) равна:
qs,d=1,6×0,35=0,56 кН/м; q s.k=1×0,35=0,35 кН/м;
g d= 0,7247×0,35=0,254 кН/м; g k= 0,6051×0,35=0,212 кН/м.
Рисунок 2 - Полная нагрузка, действующая на ребро плиты покрытия
С учетом наклона кровли полная нагрузка (рис. 2), действующая на ребро плиты, равна:
-расчетное значение – (g + q s)d= g d + qs,d cosα=0,254+0,56×0,927=0,773 кН/м;
-нормативное значение (g + q s)к= g к + qs,к cosα=0,212+0,35×0,927=0,536 кН/м
Нормальная составляющая полной нагрузки, действующая на ребро плиты, равна
(рис. 3):
fd=(g + q s)d cosα =0,773×0,927=0,716 кН/м
fk=(g + q s)k cosα=0,536×0,927=0,497 кН/м
Рисунок 3 - К определению нормальной составляющей полной нагрузки
Подсчет усилий Мd и Vd
Рисунок 4 - Расчётная схема ребра плиты
Расчётные усилия в сечениях плиты (рис.4):
изгибающий момент:
поперечная сила:
1.4 РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ
Согласно заданию принят плоский асбестоцементный лист марки ЛП-НП по ГОСТ 18124-95 в качестве обшивки. В соответствии с табл. 2.15 [3] первый сорт непрессованного плоского асбестоцементного листа имеет временное сопротивление изгибу 18 МПа. В соответствии с п. 2.3.2 [3] следует принимать временное сопротивление изгибу для расчета плиты, равное 0,9×18=16,2 МПа. Так как такого временного сопротивления изгибу в табл.2.16 [3] нет, то следует принимать значения расчетных сопротивлений асбестоцемента, находящиеся в ближайшей графе, т.е. соответствующие временному сопротивлению изгиба 16МПа. Кроме того, расчетные сопротивления следует умножать на коэффициент условий работы в соответствии с п.2.3.2 [1].Коэффициент условий работы γf = 0,9.
Следовательно, расчётное сопротивление смятию листового асбестоцемента:
fc.0.d. = 22,5·0,9=20,25МПа
Расчётное сопротивление растяжению листового асбестоцемента:
f t.0.d. = 6·0,9=5,4 МПа
Модуль упругости листового асбестоцемента:
Е = 0,1×105 МПа(табл. 2.17[3])
Расчётные характеристики древесины
Для изготовления каркаса плиты применена древесина лиственница, кроме европейской и японской, II сорта. Расчетные характеристики определены согласно табл. 2.4 [3]:
- расчётное сопротивление изгибу:
fm.d kmod·ks·kx =13·1,05·0,9·1,2=16,85 МПа
- расчётное сопротивление древесины скалыванию вдоль волокон при изгибе неклееных элементов:
fv.0.d· kmod·ks·kx = 1,6·1,05·0.9·1=1,512 МПа
- расчетное сопротивление сжатию:
fс.0.d· kmod·ks·kx = 13·1,05·0.9·1,2=16,85 МПа
- расчетное сопротивление растяжению:
fτ.0.d· kmod·ks·kx = 7·1,05·0.9·1,2=7,938 МПа
Модуль упругости древесины вдоль волокон в соответствии с п.2.1.3 [3]:
E0· kmod·kt· =10000·1,05·1=10500 МПа
где kmod =1,05 - коэффициент условий работы, принимаемый по табл. 2.6 [3];
kx - принимаемый согласно табл.2.5 [3];
ks =0,9 - коэффициент, принимаемый согласно п.2.1.2.10 [3]
1.5 ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК РАСЧЕТНОГО СЕЧЕНИЯ ПЛИТЫ
Рисунок 5 - Геометрические характеристики расчетного сечения.
Определим размеры расчетного поперечного сечения в соответствии с требованиями на стр. 117 [3] (рис 5):
b1= 18× ht,sup = 18× 8 = 144 мм < 350 / 2 =175 мм.
bd.sup=2b1=2×144=288 мм
bw = 32 мм.
hw = 100 мм.
Определим геометрические характеристики сечения:
1.Площади сечений:
Верхней сжатой обшивки – 
ребра - 
2. Статические моменты обшивок и каркаса (St.sup. Sω) относительно нижней грани (оси y):
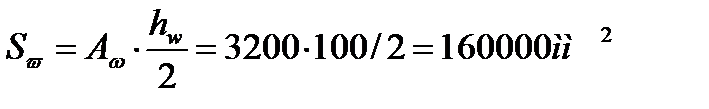
3. Положение нейтральной оси сечения конструкции без учёта податливости соединений обшивок с каркасом:
4. Приведенные (к материалу каркаса) статические моменты обшивок, относительно нейтральной оси, положение которой определялось без учёта податливости:
nw - коэффициент приведения к древесине;
5. Момент инерции ребра относительно нейтральной оси без учёта податливости:
6. Момент инерции поперечного сечения обшивки, вычисленный относительно нейтральной оси у0, положение которой определяли без учёта податливости:
7. Приведенный (к материалу каркаса) момент инерции сечения плиты, вычисленный относительно нейтральной оси у0, положение которой определяли без учёта податливости:
8.Определяем коэффициент, учитывающий распространение усилий между каркасом и обшивками:
где n1c – число срезов элементов соединений в каждом шве на половине пролёта;
Асбестоцементную обшивку прикрепляют к каркасу оцинкованными шурупами, которые обладают податливостью, необходимой для соединения разнородных материалов. По п.4.6 [3] подбираем длину и диаметр шурупов: d=4 мм, l=50 мм. По п.6.7 [4]:
Расстояние от оси шурупа до края асбестоцементной обшивки должно быть не менее 4d=4×4=16 мм и не более 10d=10×4=40 мм.
Расстояние между осями шурупов не менее 30d=30×4=120 мм и не более 30δ=30×8=240 мм.
Принимаем шаг шурупов 154 мм и расстояние от оси шурупа до края асбестоцементной обшивки 25 мм, что удовлетворяет условиям п.6.7 [4]. Общее число шурупов на одно ребро n=26, соответственно, на половине пролета nc/ =13.
η – коэффициент, определяемый по чертежу 3 [4] в зависимости от диаметра элемента соединения. При d=4 мм η =62×10-5.
km – коэффициент, принимаемый для элементов соединения из стали равным 1,0.
9. Определяем ограничение на коэффициент m:
Коэффициент m следует принимать:
При m > m0 – равным m - для расчета прочности обшивок; m0 - для расчета прочности каркаса;
При m < m0 – равным m - для расчета прочности каркаса; m0 - для расчета прочности обшивок;
Для расчета каркаса принимаем m=0,77, для расчета обшивки m=0,85.
Определение геометрических характеристик сечения с учетом податливости (m=0,85)
10. Определение нового положения нейтральной оси с учетом податливости соединения обшивки с каркасом:
11. Момент инерции поперечного сечения относительно нейтральной оси yt, положение которой определяется с учётом податливости соединений:
12. Определяем коэффициент β:
1.6 РАСЧЕТ ЭЛЕМЕНТОВ ПЛИТЫ ПО ПЕРВОЙ ГРУППЕ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ
Расчет верхней обшивки каркасной панели.
13. Напряжения в верхней обшивке определяем по формуле:
Напряжения в элементах каркасных плит не превышают расчетного сопротивления сжатию листового асбестоцемента.
Расчёт рёбер каркаса панелей.
Определение геометрических характеристик сечения с учетом податливости (m=0,77)
14. Определение нового положения нейтральной оси с учетом податливости соединений обшивок с каркасом:
15. Моменты инерции поперечного сечения относительно нейтральной оси yw, положение которой определяется с учётом податливости соединений:
16. Определяем коэффициент β:
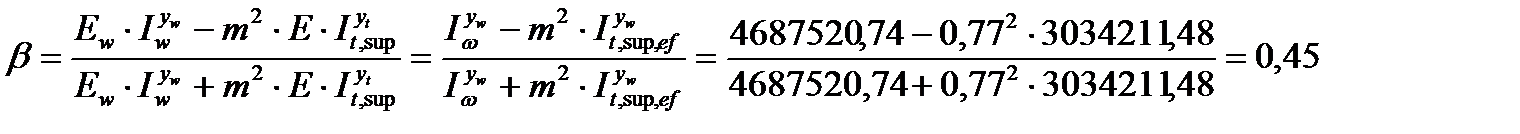
Расчет ребер каркасной панели.
17. Напряжения изгиба в каркасе определяем по формуле:
=15.8 МПа < fm.d= 16.85 МПа – напряжения в элементах каркасных плит не превышают расчётного сопротивления изгибу древесины.
18. Напряжения скалывания в каркасе при изгибе определяем по формуле:
где Ssd – статический момент сдвигаемой части поперечного сечения конструкции, приведенный к древесине, относительно нейтральной оси yw:
= 6486504,72 мм4 - момент инерции всего расчетного сечения, приведенного к древесине, относительно yw c учетом податливости (m=0.77)
= 1.46 МПа < fv.o.d. = 1,512 МПа напряжения скалывания в ребре не превышают расчётного сопротивления скалыванию вдоль волокон древесины.
1.7 ПРОВЕРКА ПРОГИБА ПЛИТЫ
Отношение допустимого прогиба плиты к пролёту не должно превышать Ulim/l≤ 1/250, определенного по эстетико-психологическим требованиям по таб. 4.1, стр. 53 [3] исходя из пролета плиты.
Прогиб плиты покрытия определяем по формуле:
Прогиб плиты не превышает предельно допустимого.
1.8 РАСЧЕТ ЭЛЕМЕНТОВ СОЕДИНЕНИЙ ОБШИВОК С КАРКАСОМ
Расчет элементов соединения обшивок с каркасом проводим, исходя из выполнения неравенства:
где m =0,85 - коэффициент, определенный для обшивок;
Ssd – статический момент сдвигаемой части поперечного сечения конструкции, приведенный к древесине, относительно нейтральной оси yw:
Ief yw =6879738.53мм4 - момент инерции всего расчетного сечения, приведенного к древесине, относительно yw c учетом податливости (при максимальном значении m=0.85):
Расчетная несущая способность одного шурупа:
где f cm - расчетное сопротивление смятию обшивки;
f h . 2. d – расчётные сопротивления смятия древесины, по табл 4.2. [3];
fn.d -расчетное сопротивление изгибу нагеля;
ka коэффициент, учитывающий угол между силой и направлением волокон, принимается по табл.4.4 [3]
t1 и t2 - соответственно толщина обшивки и древесины каркаса (8 и 32 мм соответственно) По п.6.7 [4].
d - номинальный диаметр шурупа
βn - коэффициент, зависящий от отношения толщины более тонкого элемента, к диаметру нагеля, определяемый по формуле 4.5 /6/
kn -коэффициент, зависящий от типа нагеля, табл 4.3[3]
где 
- условия прочности выполняются.
2 РАСЧЕТ И КОНСТРУИРОВАНИЕ ФЕРМЫ
Деревянные фермы – это сквозные решетчатые конструкции балочного типа, находящие значительное применение в строительстве. Они служат основными несущими конструкциями деревянных покрытий зданий различного назначения.
Древесина и сталь в деревянных фермах концентрируются в стержнях поясов и решетки, где действуют в основном продольные силы, и несущая способность этих материалов используется в наибольшей степени. Очертание и уклон верхнего пояса деревянных ферм зависят от типа кровли.
Клеедеревянные фермы заводского изготовления имеют пролеты 18…30 м и высоту, равную 1/6 пролета. Верхний пояс этих ферм имеет прямую или гнутую форму и крупное прямоугольное сечение. Ширина не превышает 17 см, а высота сечения может быть любой. Нижний пояс обычно делается стальным из 2-х стальных уголков, соединенными полками вовнутрь, и имеет такую же ширину, как и ширина верхнего пояса. Из-за стального нижнего пояса эти фермы называют металлодеревянными.
Треугольная клеедеревянная ферма с нисходящими раскосами имеет значительный уклон верхнего пояса и предназначена для покрытий с чешуйчатой кровлей. Ее верхний пояс состоит из 6 или 4 прямых стержней, соединенных в узел с эксцентриситетами для уменьшения изгибающих моментов от межузловых нагрузок. Нижний пояс делается из двух сальных уголков. Все расходы этой фермы работают только на сжатие и имеют клеедеревянное прямоугольное сечение такой же ширины, как и верхний пояс. Стойки фермы работают только на растяжение и изготавливаются из одиночных стальных арматурных стержней.
2.1 ОПРЕДЕЛЕНИЕ НАГРУЗОК НА ФЕРМУ
На ферму действуют следующие нагрузки:
- нагрузка от собственного веса покрытия и фермы;
- снеговая нагрузка (в соответствии со снеговым районом);
- снеговая неравномерная нагрузка.
- ветровая нагрузка (в соответствии с районом).
Для постоянных и временных равномерно распределенных нагрузок рассчитываем коэффициент 
(S-длинна верхнего пояса фермы; l-пролет)
Таблица 2.1 Нагрузки, действующие на 1 м 
фермы
| Наименование нагрузок | Нормативная нагрузка кН/м2 | Расчётная нагрузка кН/м2 | k | qd × k | Погонная нагрузка на ферму (шаг ферм 3,9 м) |
| Постоянная: | |||||
| - вес кровли и плиты | 0,6051 | 0,7247 | - | - | 2,826 |
| - собственный вес фермы | 0,152 | 0,1672 | 0,93 | 0,1555 | 0,606 |
| Временная: | |||||
Снеговая Sg =0,8(табл.1.8[1]);  =1, т.к. угол наклона кровли 22
qs1k=0,75
qs2k=1,25
| 0,8 0,6 1 | 1,28 0,96 1,6 | 0,93 0,93 | 0,8928 1,488 | 3,482 5,803 |
Постоянная нагрузка
Нагрузку от кровли и плит берем из таблицы 1.
Нормативный собственный вес основной несущей конструкции покрытия (фермы) вычисляется по формуле:
где å gк - нормативный вес панели покрытия, (å gк = 0,6051 кН/м2);
qк - нормативная снеговая нагрузка, (å qк = 1 кН/м2);
ksw - коэффициент собственного веса конструкции (фермы), принимаемый по табл. 1.6 [3], (ksw =3,61);
L - пролёт,(L = 24 м;)
тогда:
Расчетное значение собственного веса фермы:
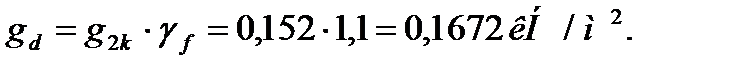
γf - коэффициент надежности по нагрузке для собственного веса фермы.
Нормативный собственный вес колонны определим по формуле:
ksw-коэффициент собственного веса конструкции (колонны) принимаемый по таблице 1.3 [3].
Расчетное значение собственного веса колонны:
γf - коэффициент надежности по нагрузке для собственного веса фермы.
Снеговая нагрузка.
Город Брест находится в IБ районе.
Полное нормативное значение снеговой нагрузки на 1 м2 горизонтальную проекцию покрытия следует определят по формуле:
S0– нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли, принимаемое в соответствии с таблицей 1.7[3].
µ - коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие, принимаемой в соответствии с таблицей 1.9 [3].
Рассмотрим два варианта снеговой нагрузки:
- равномерная снеговая нагрузка:
- qsk= 4,68 кн/м4
- неравномерная снеговая нагрузка:
qs1k = 3,482 кн/м, qs2k = 5,803 кн/м;
Рисунок 2.1 – Варианты нагружения снеговой нагрузкой.
Ветровая нагрузка.
Нормативное значение средней ветровой нагрузки:
где, w0 – нормативное значение ветрового давления, принимаемое в зависимости от ветрового района (IV) по данным табл.1.10, и составляет 0,48 кН/м2;
к – коэффициент, учитывающий изменение ветрового давления по высоте, принимаемый по табл.1.11[3];
с – аэродинамический коэффициент, принимаемый по табл.1.12[3].
Аэродинамические коэффициенты:
Се=+0,8 – для наветренной поверхности;
Се1= - 0,57;
Се2= -0,57;
Се3=-0,475.
Рисунок 2.2: Расчётная схема от действия ветровой нагрузки
Коэффициент надежности для ветровой нагрузки γqw=1,4.
Боковые зоны ветрового давления ограниченны точками, имеющими ординаты:
| Y=0 | k=0 |
| Y=5м | k=0,5 |
| Y=10м | k=0,65 |
| Y=20м | k=0,85 |
| y=21 | k=0,86 |
| Y=25.8 | k=0,92 |
Таблица 2-2 – Ветровая нагрузка по высоте.
| Участки | Нормативное значение ветрового давления | k | c | Коэффициент надежности | Расчетное значение ветрового давления | Расчетная нагрузка на погонный метр |
| До 5 м | 0,48 | 0,5 | 0,8 | 1,4 | 0,2688 | |
| До 10 м | 0,65 | 0,8 | 0,3494 | |||
| До 20 м | 0,85 | 0,8 | 0,4569 | |||
| До 21 м | 0,86 | 0,8 | 0,4623 | |||
| До 25,8 м | 0,92 | -0,57 | -0,3524 | |||
| До 21 м | 0,48 | 0,86 | -0,475 | 1,4 | -0,2745 | |
| До 20 м | 0,85 | -0,475 | -0,2713 | |||
| До 10 м | 0,65 | -0,475 | -0,2075 | |||
| До 5 м | 0,5 | -0,475 | -0,1596 |
Для упрощения расчёта фактическую ветровую нагрузку заменяем эквивалентной, равномерно распределенной по высоте колонны. Величину эквивалентной нагрузки находим из условия равенства изгибающих моментов в защемлённой стойке от фактической эпюры ветрового давления и от равномерно распределённой нагрузки..
Найдем эквивалентную равномернораспределенную нагрузку на раму с наветренной стороны:
С подветренной стороны:
Найдем эквивалентную равномернораспределенную нагрузку на раму с наветренной стороны:
С подветренной стороны:
Расчетная сосредоточенная ветровая нагрузка выше отметки 21 м:
с наветренной стороны
С подветренной стороны:
Сочетание нагрузок
Сочетание № 1: постоянная нагрузка +снеговая нагрузка (равномерно распределенная)+ветровая нагрузка.
Таблица 2.3 – Расчетные значения при нагружении №1
Nmax=-357,072 кН – в 8 стержне верхнего пояса.
Сочетание № 2: постоянная нагрузка +снеговая нагрузка (не равномерно распределенная)+ветровая нагрузка.
Таблица 2.4 – Расчетные значения при нагружении №2
Nmax=-271,598 кН – в 8 стержне верхнего пояса.
Из сравнения сочетаний 2-х видов нагрузок видно, что 1-й вид нагрузки больше 2-й и
=271,598 кН < 
=357,072 кН.
Следовательно, принимаем в расчетах 
= 357,072 кН.
2.2 ВЫБОР СВЯЗЕЙ ДЛЯ ДЕРЕВЯННЫХ КАРКАСНЫХ ЗДАНИЙ
Несущие конструкции каркаса представляют собой плоские системы (в данном случае – фермы и колонны), которые рассчитаны на восприятие нагрузок, действующих только в их плоскости. Сооружение, выполненное только из одних плоских несущих элементов, расположенных в вертикальных плоскостях, будет геометрически изменяемы в пространстве. Поэтому для обеспечения пространственной жесткости и геометрической неизменяемости, плоские конструкции объединяют между собой в геометрически неизменяемый пространственный каркас при помощи связей.
Конструктивно связи выполняются из стержней, объединенных в треугольник.
В каркасных зданиях связи выполняют следующие функции:
1 создание геометрической неизменяемости сооружения;
2 обеспечение устойчивости сжатых элементов путем уменьшения их расчетной длины;
3 восприятие нагрузок, действующих из плоскости несущих конструкций (давление ветра, торможение крана и т.д.)
4 перераспределение нагрузок между элементами каркаса;
5 фиксирование положения и обеспечение устойчивости конструкции во время монтажа.
В моём здании для обеспечения пространственной жёсткости и устойчивости, приняты следующие связи: для обеспечения поперечной устойчивости колонн, устанавливают вертикальные связевые фермы, с высотой кратной ширине плит покрытия-2,26м., в пролётах 1-2;5-6;10-11.
Для обеспечения поперечной неизменяемости ферм, по верхнему поясу стропильных ферм устанавливаем скатные связевые фермы с шагом кратным - 2,264м. Устанавливают эти горизонтальные связевые фермы в пролётах 1-2;5-6;10-11 тяжей с муфтами.
2.3 РАСЧЕТ И КОНСТРУИРОВАНИЕ ВЕРХНЕГО ПОЯСА ФЕРМЫ
Расчет ведем по максимальному усилию, возникающему в стержне № 8 верхнего пояса фермы. В соответствии с таблицей 2.3 усилие в стержне № 8:
=357,072 кН = 0,357 МН
Принимается клеедеревянное сечение из досок 1-го сорта шириной b=20 см.
Расчетное сопротивление древесины сжатию вдоль волокон:
по таблице 2,4 (1).
Расчётное сопротивление древесины сжатию вдоль волокон для лиственницы (кроме европейской и японской). С учётом коэффициентов 
и 
(коэффициент условий работы по таблице 2,5(1)):
Приближённо требуемая площадь сечения:
где 0,6 – коэффициент, учитывающий влияние изгибающего момента и прогиба.
Требуемая высота сечения:
Принимается сечение: 
Сечение верхнего пояса фермы принимаем из 8-и досок с исходной толщиной 
, а после фрезерования 26 мм и шириной 
, в итоге окончательное сечение с учетом фрезеровки после склейки составит 208×200 мм А=0,0416 м2.
Верхний пояс фермы является сжато-изгибаемым элементом, соответственно расчёт ведём по формуле 7.31(3):
где 
- расчётное напряжение сжатие;
- расчётное сопротивление сжатию;
- расчётное напряжение изгиба;
- коэффициент, учитывающий увеличение напряжений при изгибе от действия продольной силы;
определяется по формуле 7.33(3):
где 
- площадь поперечного сечения элемента;
определяем, учитывая требование 7.1.9.2.(3) по формуле 7.32(3):
где 
- коэффициент продольного изгиба, определяемый в соответствии с п.7.1.4.2(3).
Для этого сначала определим гибкость верхнего пояса по формуле 7.16(3):
где 
- расчётная длина элемента;
- радиус инерции сечения элемента: 
.
Тогда: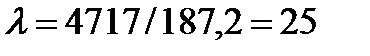 
;
= 100 не превышает предельную гибкость 
=120 приведенной в таблице 7.2 
.
В соответствии с п. 7.1.4.2 
элементы с 
35 следует проверять на устойчивость по формуле 7.11 
:
Так как λ=25<35 проверку на устойчивость можно не производить.
2.4 РАСЧЕТ НИЖНЕГО ПОЯСА ФЕРМЫ
Нижний пояс работает на растяжение. Расчётное продольное усилие в нижнем поясе принимаем по таблице 2.3 сочетаний нагрузок:
(1 стержень). Нижний пояс фермы конструируем стальным. Сталь класса С235. Расчётное сопротивление стали 
(1 приложение 4)
Требуемая площадь сечения нижнего пояса:
По таблице сортамента прокатных профилей принимаем два равнополочных уголка 63 
6 мм суммарной площадью 
где 
- площадь сечения нижнего пояса. 
.
2.5 РАСЧЕТ И КОНСТРУИРОВАНИЕ РАСКОСА ФЕРМЫ
Все раскосы фермы работают на сжатие. Подбирается и проверяется сечение раскоса № 12, так как в нём действует наибольшая сжимающая сила: 
Предварительно принимаем сечение раскоса по приложению 5(3). Ширину сечения раскоса принимаем такую - же, как в верхнем поясе фермы 
, а толщину 
, в 6 слоя склеенных досок. Тогда высота сечения будет:
Соответственно, площадь поперечного сечения:
Гибкость раскоса определяем по формуле 7.16(3);
- расчётная длинна.
где 
- радиус инерции сечения;
= 104 не превышает предельную гибкость =120 приведенной в таблице 7.2 .
В соответствии с п. 7.1.4.2 элементы с 35 следует проверять на устойчивость по формуле 7.11 :
где 
- расчетное сжимающее напряжение, определяемое по формуле 7.12 
:
- расчётное сопротивление сжатию.
- коэффициент продольного изгиба, определяемый в зависимости от гибкости элемента.
При 
, 
определяем по формуле 7.14(3):
Следовательно, подставив данные в формулу 7.11(3) получим:
.
Условие 7.1 (3) выполняется, следовательно устойчивость сжатого раскоса обеспечена и принятое сечение оставляем для дальнейших расчетов.
2.6 РАСЧЕТ И КОНСТРУИРОВАНИЕ СРЕДНЕЙ СТОЙКИ ФЕРМЫ
Растягивающая сила, действующая в среднем стержне (стойке) № 10 равна: 
взятая из таблицы 2.3 сочетания нагрузок, как максимальная сила, действующая в стойках фермы. Т.к. стойка работает на растяжение, то сечение принимается из одиночной стальной арматуры. Принимаем арматуры класса S240 с нарезками на концах. Расчётное сопротивление стали 
Коэффициент концентрации напряжений в нарезке: 
Определяем требуемую площадь
: 
В зависимости от полученной площади подбираем по сортаменту диаметр стальной арматуры: диаметр=22мм с расчётной площадью 
.
Т.к. условие выполняется, следовательно принимаем подобранное сечение стойки.
2.7 КОНСТРУИРОВАНИЕ И РАСЧЕТ УЗЛОВ ФЕРМЫ
Коньковый узел решается при помощи стального крепления с диафрагмой треугольного сечения, в которую упирается торец верхнего пояса и опирается шайба тяжа средней стойки.
Промежуточные узлы верхнего и нижнего поясов фермы решаются с помощью стальных креплений, присоединение к которым сжатых раскосов производится лобовыми упорами и болтами.
Подбор площади сечения торцов лобовых упоров раскосов при смятии вдоль волокон. Максимальная сжимающая сила 
Расчётное сопротивление древесины сжатию вдоль волокон: 
с учётом коэффициентов 
и 
:
;
Требуемая площадь смятия:
Принятые размеры сечения: 200×156мм
Расчётная площадь сечения: 
Проверка выполняется.
Болтовые соединения металлических пластин с древесиной расчитываются в зависимости с п. 9.4.68, 9.4.61, 9.4.1.14 (соединения нагельного типа).
Расчетную несущую способность односрезного надела следует принимать равной наименьшему значению из формул:
где 
расчетное сопротивление смятию древесины в глухом нагельном гнезде для односрезных соединений, принимаемый по табл. 9.1 (3): 
толщина более тонкого элемента в односрезных соединениях: 
диаметр нагеля: 
коэффициент, учитывающий угол 
между силой и направлением волокон; определяемый по табл. 9.3 (3)
максимальное значение коэффициента, зависящего от отношения толщины более тонкого элемента к диаметру нагеля, принимаемое в соответствии с п. 9.4.8.3: 
- расчётное сопротивление изгибу нагеля, определяемое в соответствии с п.9.4.8.3: 
с учётом коэффициентов 
и 
:
Тогда: 
Следовательно количество нагелей в соединении можно определить по формуле 9.6(3):
;
где 
- расчётная несущая способность соединения на цилиндрических нагелях из одного материала и одинакового диаметра.
- количество швов в соединении для одного нагеля (в нашем случае 
);
Тогда 
болтов;
болта;
где 
и 
- количество нагелей по оси 1 и 2;
и 
- расчётная несущая способность соединения на цилиндрических нагелях 1 и 2 оси.
Тогда 
По таблице 9.5(3) определяем min расстояния между болтами и между кромкой и болтами:
;
3 РАСЧЕТ И КОНСТРУИРОВАНИЕ КОЛОННЫ ПОСТОЯННОГО СЕЧЕНИЯ
Расчётную схему колонны принимаем: в плоскости Х-Х с жестким соединением низа колонны и шарнирным закреплением верха; в плоскости У-У с шарнирным закреплением верха и низа.
Подбор сечения. Принимаем ширину колонны исходя из конструктивных требований 175мм без учёта острожки после склеивания, а с учётом острожки она составит 168мм.
Исходные данные:
В соответствии с таблицей 2.3 наибольшее усилие в стержне №14 
Расчетное сопротивление древесины сжатию вдоль волокон:
по таблице 2,4 (1).
Расчётное сопротивление древесины сжатию вдоль волокон для лиственницы (кроме европейской и японской). С учётом коэффициентов и (коэффициент условий работы по таблице 2,6(1)):
Приближённо требуемая площадь сечения:
где 0,6 – коэффициент, учитывающий влияние изгибающего момента.
Требуемая высота сечения:
Следовательно, высота сечения h=0,1м, однако исходя из конструктивных требований принимаем сечение колонны 168×600мм из досок первоначальным сечением 175х32мм в количестве 23шт.
3.1 РАСЧЕТ В ПЛОСКОСТИ Х - Х
Геометрическая высота колонны, в соответствии с исходными данными:
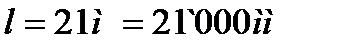
Для принятой расчётной схемы, учитывая п.7.1.4.4(3), расчётная длина колонна определяется по формуле 7.17(3):
где 
- коэффициент, принимаемый по таблице 7.1(3). 
Следовательно: 
Колонна является сжато-изгибаемым элементом расчёт ведём в соответствии с пунктом 7.1.9.(3). В соответствии с п. 7.1.9.1(3) при изгибе с осевым сжатием должно удовлетворяться следующее условие 7.31(3):
где где 
по формуле 7.12(3) – расчётное сжимающее напряжение вдоль волокон древесины;
- из табл. 2.3 стержень №14;
- расчётное напряжение изгиба, определяемое по формуле 7.22(3):
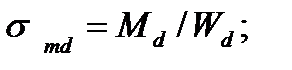
где 
- расчётный изгибающий момент относительно соответствующей оси (оси х) принимаем по таблице 2.3 =265,201кНм;
момент сопротивления сечения:
Тогда: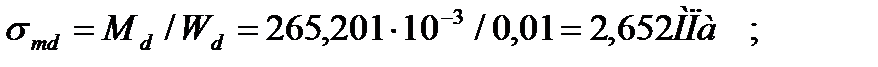 
- коэффициент, учитывающий увеличение напряжений при изгибе по направлению соответствующей оси от действия продольной силы, определяемой по формуле 7.32(3):
Гибкость колонны определяем по формуле 7.16(3);
где 
- радиус инерции сечения;
При 
, определяем по формуле 7.14(3):
Тогда подставляя все найденные значения в формулу 7.31(3) получим:
Условие прочности по оси Х-Х выполняется.
3.2 РАСЧЕТ В ПЛОСКОСТИ У - У
Геометрическая высота колонны, в соответствии с исходными данными:
Для принятой расчётной схемы, учитывая п.7.1.4.4(3), расчётная длина колонна определяется по формуле 7.17(3):
где - коэффициент, принимаемый по таблице 7.1(3). 
Следовательно: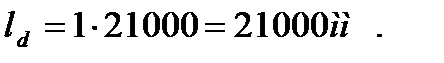 
Определяем положение центра тяжести колонны: так как колонна постоянного по высоте сечения, то соответственно центр тяжести колонны будет посередине её длины.
Проводим центральные оси продольного сечения колонны. Колонна является изгибаемым элементом, в соответствии с п.7.1.4.3(3) гибкость элемента определяется по формуле 7.16(3):
где 
- радиус инерции сечения;
Полученная гибкость 
превышает предельную 
(таблица 7.2(3)), в связи с этим увеличиваем ширину колонны до 620мм с учётом фрезеровки после склеивания.
где 
- радиус инерции сечения;
Полученная гибкость 
не превышает предельную (таблица 7.2(3))
В соответствии с пунктом 7.1.4.2(3) элементы с 
проверяются на устойчивость по формуле 7.11(3):
где по формуле 7.12(3) – расчётное сжимающее напряжение вдоль волокон древесины;
- из табл. 2.3 стержень №14;
