Двухуровневое управление потоком заданий в серверной системе
 |
Рис. 1 Зависимость интенсивности потока ответов сервераμот числа ожидающих обработки или обрабатываемых в данный момент запросов n при гистерезисном управлении
Для гистерезисного управления работа системы определяется параметрами 
и 
, притом 
,, 
- интенсивность потока запросов, 
и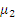 
- интенсивности потока ответов сервера для двух режимов работы.
Отличие от системы с одноуровневым управлением заключается в том, что переход между режимами работы серверной системы происходит, когда количество запросов к серверу, ожидающих обработки либо обрабатываемых в данный момент (длина очереди), достигает значения L2. Обратный переход в режим работы без кеширования происходит, когда длина очереди уменьшается до значения L1.
Пусть 
, 
, тогда 
, 
.
Состояния системы определяются числом находящихся в системе запросов 
(длина очереди) и режимом работы (с кешированием или без кеширования).
Для состояний, соответствующих работе с первым сервером, каждому состоянию с длиной очереди 
при 
, где 
поставим в соответствие число .
Для состояний, соответствующих работе со вторым сервером, каждому состоянию с длиной очереди при 
, поставим в соответствие число 
.
Далее изображен граф цепи Маркова, который описывает число запросов N(t), находящихся в системе (ожидающих обработки, либо обрабатываемых в данный момент) в момент времени t. Вершинам графа соответствуют стационарные вероятности нахождения процесса N (t) в конкретном состоянии, пронумерованные в соответствии с нумерацией состояний системы, а дугам — интенсивности переходов между состояниями.
 |
Рис. 2 Граф, описывающий переходы между состояниями процесса N(t) с различной длиной очереди при использовании гистерезисного управления
Определение показателей качества функционирования серверной системы с двухуровневым управлением потоком заданий
Соотношения для стационарных вероятностей 
введенных состояний получены по аналогии с одноуровневым управлением.
Стационарная вероятность 
вычисляется из условия
| (1) |
которое после подстановки выражений для 
можно свести к следующему виду
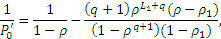
| (2) |
Формулы для стационарного распределения числа находящихся в системе запросов (длины очереди) получаются, исходя из соотношений
| (3) |
и имеют следующий вид:
| (4) |
Производящая функция от стационарного распределения длины очереди
| (5) |
где
| (6) |
Средняя длина очереди, т.е. среднее количество запросов к серверу, находящихся в системе (ожидающих обработки, либо обрабатываемых в данный момент)
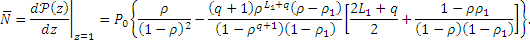
| (7) |
Поскольку из всех находящихся в системе запросов в любой момент времени t один и только один запрос находится на обработке, то для любого 
число ожидающих обработки запросов 
связано с количеством всех находящихся в системе запросов 
следующим соотношением:
| (8) |
Следовательно, производящая функция стационарного распределения числа запросов, ожидающих обработки связана с найденными ранее производящими функциями 
и 
соотношением
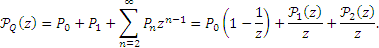
| (9) |
Таким образом,
| (10) |
среднее число ожидающих обработки запросов
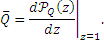
| (11) |
Связь между средним временем ответа 
и средним числом находящихся в системе запросов 
задает одна из формул Литтла: 
. Аналогичным соотношением связаны между собой среднее время ожидания 
и среднее число ожидающих обработки запросов: 
Длительность обслуживания позволяет вычислить следующее соотношение:
Время ответа (T) = время ожидания (W) + длительность обслуживания (S).
Среднее время простаивания в очереди при гистерезисном управлении:
| (12) |
среднее время обслуживания при гистерезисном управлении:
| (13) |
где 
, 
| (14) |
