Ускорение буксира при свободном движении 4 страница

При полном геометрическом подобии получаем соотношения:

Отметим, что сам коэффициент теплоотдачи зависит от размеров тела.

Коснемся кратко вопроса подобия динамических процессов в электроприводах. Пусть имеется базовый электропривод постоянного тока. При подаче на обмотку якоря напряжения U ₀ его скорость вращения изменяется по закону ω₀(t ₀). Имеется электропривод постоянного тока сравнения. При подаче на обмотку якоря напряжения U его скорость вращения изменяется по закону ω(t). Как видно, время электроприводов обозначено по-разному.

Обозначим

Коэффициент подобия по времени γ _t будем считать постоянным. Если при некотором соотношении между параметрами электроприводов коэффициент подобия по скорости вращения γ_ω постоянен, то электроприводы назовем динамически подобными. Иначе говоря, при этом можно подобрать такие масштабы для времени и скорости вращения, что графики ω(t) и ω₀(t) совпадут.

Пусть базовый электропривод имеет уравнения

(23.25)

(23.26)

Электропривод сравнения описывается уравнениями

(23.27)

(23.28)

Характеристическое уравнение для системы дифференциальных уравне-

ний (23.25), (23.26) имеет вид

где

Аналогично характеристическое уравнение для системы дифференциальных уравнений (23.27), (23.28) имеет вид

где

Чтобы графики переходных процессов в электроприводах были подобны, необходимо, чтобы совпали отношения электромагнитной и электромеханической постоянных времени:

откуда следует основное условие динамического подобия электроприводов:

(23.29)

Коэффициент подобия по времени можно определить из равенства

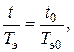
откуда следует

(23.30)

Коэффициент подобия по скорости вращения можно определить по сравнению установившихся скоростей:

(23.31)

На рис. 23.3 представлены графики скорости базового электропривода и электропривода сравнения при значениях коэффициентов подобия и

 

 

Рис. 23.3. Графики скоростей вращения

в динамически подобных электроприводах

 

 

ЛЕКЦИЯ 24

Подобие электромагнитных устройств

и электрических машин

Рассмотрим два геометрически подобных двухобмоточных трансформатора. У трансформатора сравнения обозначим: S _c – площадь поперечного сечения стали (магнитопровода); S _о – площадь окна под обмотки; f – частота напряжения; k _з.м – коэффициент заполнения окна медью; j – плотность тока в обмотках; B_m – амплитуда магнитной индукции в стали; w ₁, w ₂ – числа витков первичной и вторичной обмоток; Ф _m – амплитуда основного магнитного потока. Электромагнитная мощность первичной обмотки определяется выражениями:

P _эм = E ₁ I ₁ = 4,44 f Ф _m w ₁ I ₁ = 4,44 f (S _c B_m) (S _о k _з.м j /2) = 2,22 k _з.м f S _c S _о B_m j.

Предполагается, что первичная обмотка занимает половину площади окна.

Видно, что электромагнитная мощность пропорциональна частоте питания, произведению площадей стали и окна под обмотки, а также амплитуде магнитной индукции и плотности тока в обмотках. Получаем формулу связи для двух подобных трансформаторов:

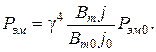(24.1)

Как было показано ранее, при увеличении размеров мощность потерь растет пропорционально третьей степени размеров, а площадь поверхности охлаждения – лишь второй степени размеров. Потребуем, чтобы температура обмоток трансформаторов была одинаковой. Имеем соотношения:

P = ρ j ² V _м,

Отсюда следует:

или

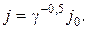(24.2)

Подставляя это соотношение в формулу электромагнитной мощности, получаем

(24.3)

Рассмотрим электромагнит постоянного тока (см. рис. 20.3). Магнитодвижущая сила его обмотки

Магнитная индукция в воздушном зазоре

Сила тяги электромагнита

Собирая эти формулы в одну, получаем

Приходим к выводу, что усилие пропорционально четвертой степени размеров:

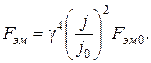(24.4)

При условии сохранения температуры обмотки при переходе от базового электромагнита к электромагниту сравнения следует учитывать соотношение (24.2), согласно которому получаем

(24.5)

Рассмотрим электродвигатель постоянного тока независимого возбуждения. Его электромагнитный момент

где с – конструктивный коэффициент; Ф – основной магнитный поток; I – ток якоря. Полагая количество проводников якоря фиксированным, получаем:

где плотность тока j по условию сохранения температуры определяется форму

лой (24.2)

Ток обмотки возбуждения по аналогичной причине имеет плотность

Тогда МДС обмотки возбуждения

Напряженность магнитного поля получается делением МДС на длину средней силовой линии, откуда следует

Подставляя полученные выражения для плотности тока якоря и для магнитной индукции в формулу момента, получаем:

(24.6)

При проектировании электродвигателей постоянного тока применяется линейная нагрузка А, равная току, приходящемуся на единицу длины дуги якоря. При геометрическом подобии машин эта величина пропорциональна диаметру якоря при фиксированной плотности тока. Следовательно,

Графики относительных величин j, A и B приведены на рис. 24.1. За единицу приняты их значения у базового электродвигателя.

 

 

Рис. 24.1. Зависимости относительных значений плотности тока, линейной

нагрузки и магнитной индукции в зазоре от коэффициента подобия

У двигателя постоянного тока с возбуждением от постоянных магнитов выполняются соотношения

откуда следует

(24.7)

Поэтому двигатели постоянного тока с возбуждением от постоянных магнитов применяются при сравнительно небольших размерах.

Рассмотрим синхронный двигатель с электромагнитным возбуждением. Из условия сохранения температуры обмоток якоря и возбуждения получаем

Магнитная индукция в зазоре и основной магнитный поток удовлетворяют равенствам

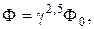
а при сохранении числа витков ток обмотки якоря (статора)

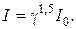
Электромагнитный момент синхронного двигателя

где с – конструктивный коэффициент; θ – угол между продольной осью ротора и осью МДС обмотки статора. Подставляя сюда выражения для Ф и I, получаем

(24.8)

У синхронного двигателя с возбуждением от постоянных магнитов выполняются соотношения

откуда следует

Поэтому двигатели с возбуждением от постоянных магнитов применяются при сравнительно небольших размерах.

Рассмотрим трехфазный асинхронный двигатель с короткозамкнутым

ротором. Его электромагнитный момент определяется выражением

где с – конструктивный коэффициент; Ф – основной магнитный поток; I ₂ – ток фазы обмотки ротора; φ₂ – угол сдвига по фазе между ЭДС и током в роторе. Полагая

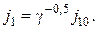
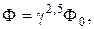
получаем

(24.9)

Следует отметить, что у крупных машин величина магнитной индукции ограничивается насыщением, и показатель степени несколько снижается.

Вернемся к двигателю постоянного тока и рассмотрим два важных динамических параметра – электромагнитную и электромеханическую постоянные времени. Электромагнитная постоянная времени

Здесь L – индуктивность обмотки якоря; r – ее активное сопротивление; W _м – энергия магнитного поля реакции якоря; P – мощность потерь в обмотке якоря.Энергия магнитного поля определяется выражением

откуда следует

С учетом формулы для мощности

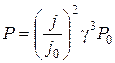
приходим к выводу, что

Итак, при увеличении всех размеров вдвое электромагнитная постоянная времени двигателя возрастает в 4 раза.

Займемся теперь электромеханической постоянной времени. Она определяется формулой

С учетом выражений

приходим к равенству

При пропорциональном изменении размеров двигателя постоянного тока его электромеханическая постоянная времени не изменяется. Отметим, что в электроприводе электромеханическая постоянная времени зависит от суммарного момента инерции ротора двигателя и объекта управления.

ГЛАВА VI