Кафедра экономической теории и национальной экономики
Курсовая работа
По дисциплине: математические методы и модели исследования операций в экономике
Тема: Оптимизация производственно-отраслевой структуры сельскохозяйственного предприятия в Ордена Трудового Красного Знамени племзавод-колхозе имени 50-летия СССР
Выполнила: студентка
группы ЭММ-31
Кивитар Т. С.
Проверила: Ярыгина Л. В.
Вологда
Оглавление
Введение-------------------------------------------------------------------------------------------- 3
1. Математическое моделирование экономических процессов сельском хозяйстве 5
1.1. Теоретические основы математического моделирования экономических процессов--------------------------------------------------------------------------------------------------------- 5
1.2. Применение математического моделирования в сельском хозяйстве. Планирование оптимальной производственно-отраслевой структуры сельскохозяйственного предприятия------------------------------------------------------------------------------------- 10
2. Характеристика Ордена Трудового Красного Знамени племзавод-колхоза имени 50-летия СССР-------------------------------------------------------------------------------------- 15
3. Оптимизация производственно-отраслевой структуры------------------------- 19
3.1. Разработка числовой экономико-математической модели------------------- 19
3.2. Экономическая интерпретация оптимальной производственно-отраслевой структуры------------------------------------------------------------------------------------------------------- 23
3.3. Эффективность применения оптимальной производственной структуры производства------------------------------------------------------------------------------------------------------- 26
Заключение--------------------------------------------------------------------------------------- 29
Список использованной литературы----------------------------------------------------- 31
Введение
Сельскохозяйственная продукция востребована во все времена. Однако в последнее время сельское хозяйство переживает не лучшие времена. Поэтому важно найти новые подходы к планированию экономики как в отрасли в целом, так и на отдельных предприятиях. Одним из таких подходов может служить математическое моделирование экономических процессов в сельском хозяйстве. Применение экономико-математического моделирования позволяет выбрать оптимальный вариант с точки зрения выбранного критерия, который при этом удовлетворяет необходимым требованиям и условиям.
В системе моделей оптимального планирования сельского хозяйства на уровне предприятия центральное место занимает модель оптимизации производственно-отраслевой структуры. Она дает возможность определять основные параметры развития производства для текущего и перспективного планирования, может использоваться для анализа сложившейся структуры производства, позволяющего выявить более целесообразные пути использования ресурсов и возможности увеличения объемов производства продукции, опираясь на фактические данные за предшествующие годы.
Именно поэтому целью данной курсовой работы является определение оптимальной специализации производства и сочетания отраслей в сельскохозяйственном предприятии.
Задачи, которые необходимо решить для достижения поставленной цели:
– изучить теоретические основы моделирования оптимальной производственно-отраслевой структуры;
– дать общую характеристику объекта исследования;
– разработать экономико-математическую модель оптимизации производственно-отраслевой структуры сельскохозяйственного предприятия;
– рассчитать и выполнить анализ оптимальной производственно-отраслевой структуры предприятия;
– оценить эффективность полученной оптимальной структуры и сравнить ее с существующей на предприятии.
Объектом исследования в курсовой работе является Ордена Трудового Красного Знамени племзавод-колхоз имени 50-летия СССР.
В первой главе «Математическое моделирование экономических процессов сельском хозяйстве» приведены теоретические аспекты моделирования производственных процессов, в частности, особенности применения экономико-математического моделирования в сельском хозяйстве.
Во второй главе «Характеристика Ордена Трудового Красного Знамени племзавод-колхоза имени 50-летия СССР» дана общая характеристика объекта исследования, приведены показатели его хозяйственной деятельности.
В третьей главе «Оптимизация производственно-отраслевой структуры» построена математическая модель оптимизации производственно-отраслевой структуры, найдено оптимальное решение, выполнен анализ полученных данных. Также проведено сравнение эффективности применения в хозяйстве фактической и оптимальной производственно-отраслевой структуры.
Основными источниками информации являются: литература по вопросам математического моделирования в сельском хозяйстве, основные формы годовой бухгалтерской отчетности предприятия, нормативные справочники по сельскому хозяйству.
Исследование проводилось при помощи методов экономико-математического моделирования, экономико-статистического анализа, теории двойственности, табличного представления данных. Все расчеты были выполнены на ЭВМ.
1. Математическое моделирование экономических процессов сельском хозяйстве
1.1. Теоретические основы математического моделирования экономических процессов
Любая социально-экономическая система представляет собой сложную систему, в которой взаимодействуют десятки и сотни экономических, технических и социальных процессов, постоянно изменяющихся под воздействием внешних условий, в том числе и научно-технического прогресса. В таких условиях управление социально-экономическими и производственными системами превращается в сложнейшую задачу, требующую специальных средств и методов.
Моделирование – один из наиболее распространенных способов изучения вышеназванных процессов и явлений. Моделирование основывается на принципе аналогии и позволяет изучать объект при определенных условиях и с учетом неизбежной односторонней точки зрения. Объект, трудно доступный для изучения, изучается не непосредственно, а через рассмотрение другого, подобного ему и более доступного – модели. По свойствам модели обычно оказывается возможным судить о свойствах изучаемого объекта. Но не обо всех свойствах, а лишь о тех, которые аналогичны и в модели, и в объекте и при этом важны для исследования. Такие свойства называются существенными.
В самом общем смысле модель – это упрощенное подобие исследуемой системы, обладающее существенными ее свойствами и соотношениями. Модель используется как условный образ, сконструированный для упрощения исследования объекта.
Экономико-математическая модель оказывается в этих условиях основным средством экспериментального исследования экономики, так как обладает следующими свойствами:
– имитирует реальный экономический процесс (или поведение объекта);
– обладает относительно низкой стоимостью;
– может многократно использоваться;
– учитывает различные условия функционирования объекта.
Модель может и должна отражать внутреннюю структуру экономического объекта с заданных (определенных) точек зрения, а если она неизвестна, то лишь его поведение.
В литературе нет устоявшегося определения экономико-математической модели. Возьмем за основу следующее определение. Экономико-математическая модель – математическое описание экономического процесса или объекта, осуществленное в целях их исследования или управления ими; математическая запись решаемой экономической задачи (поэтому часто термины задача и модель употребляются как синонимы).
Возможны и другие определения экономико-математической модели:
1. Специальная конструкция показателей и параметров, объединяемая (в явном или неявном виде) системой уравнений в единое целое.
2. Некоторое математическое выражение, состоящее из совокупности связанных между собой математическими (количественными) зависимостями математических величин, все или часть из которых являются экономическими величинами.
3. Математическое описание планово-экономической задачи, позволяющее осуществить законченный цикл расчета ее параметров на основе внешних (исходных) данных.
Отмечая сложность формулировки всеобъемлющего определения, будем в дальнейшем понимать под экономико-математической моделью совокупность взаимосвязанных математических зависимостей (уравнений или неравенств), формально отражающих условия функционирования реальных экономических объектов. Другими словами, экономико-математическая модель – это математическое отображение исследуемого экономического объекта (процесса), с помощью которого изучается его функционирование и оценивается изменение его эффективности при возможных изменениях входных характеристик. Многократная же реализация экономико-математических моделей в этом процессе и называется экономико-математическим моделированием. Таким образом, под экономико-математическим моделированием будем понимать в дальнейшем построение и изучение с помощью средств вычислительной техники экономико-математической модели, способной заменить исследуемый объект.
Экономико-математическое моделирование дает возможность находить истину не методом дорогостоящих «проб и ошибок», а формулировать рекомендации по управлению экономикой, опираясь на прочный фундамент научного предвидения. Работа с моделью, а не с объектом, оборачивается оперативным получением подробной и наглядной информации, вскрывающей его внутренние связи, количественные характеристики и качественные параметры. Многократно уменьшаются материальные и трудовые затраты, присущие экспериментальным подходам, дающим, как правило, лишь крупицы нужной информации. [2]
Конечно, следует иметь в виду, что модель всегда проще оригинала. Исследователь стремится воспроизвести прежде всего те свойства системы, которые важны для решения стоящих перед ним задач. Степень достоверности выводов при этом зависит от детализации исходной информации о свойствах системы, глубины проработки и изученности закономерностей поведения этой системы. Модели сами по себе не могут раскрыть характер экономических взаимосвязей. Они лишь воспроизводят поведение системы на том уровне знаний, который достигнут конкретными науками в моделируемых явлениях. При разработке экономико-математической модели развития хозяйства на перспективу необходимо знать конкретные технологические особенности производства продукции растениеводства и животноводства, формы его организации, возможные объемы ресурсов и ограничивающие условия, влияющие на развитие производства.
В зависимости от характера моделируемых объектов и процессов структура моделей может быть различной. В то же время имеются общие элементы, которые можно выделить.
Базовая модель включает следующие элементы: исходные значения ресурсов; переменные величины, значения которых должны определяться в результате моделирования; технико-экономические коэффициенты и нормативы, необходимые для отображения закономерных взаимосвязей ресурсов с выходными показателями; условия (ограничения), описывающие характер и логику взаимосвязей в модели; критерий оптимальности, определяющий качество функционирования исследуемой системы.
В зависимости от необходимости учета в модели тех или иных особых условий различают модели линейного, нелинейного, целочисленного, параметрического программирования или смешанные.
Разработка экономико-математической модели осуществляется поэтапно в определенной последовательности. Так как в дальнейшей работе нам понадобится линейная модель, основные этапы моделирования рассмотрим на примере построения линейной экономико-математической модели:
1. Постановка задачи и обоснование критерия оптимальности. Постановка задачи предполагает четкую экономическую формулировку, включающую цель решения, установление планового периода, выяснение неизвестных параметров объекта и тех, количественное значение которых нужно определить, их производственно-экономических связей, а также множества факторов и условий, отражающих моделируемый процесс.
Цель решения задачи выражается количественно конкретным показателем, называемым критерием оптимальности. Он должен соответствовать экономической сущности решаемой задачи.
Для разработки линейной экономико-математической модели требуется соблюдение ряда условий:
а) Предполагается, что связи и зависимости моделируемого процесса носят линейный характер и их можно описать системой линейных уравнений и неравенств.
б) Система линейных уравнений и неравенств, характеризующая совокупность условий экономического процесса, должна иметь множество решений, то есть быть неопределенной и совместной.
в) Поскольку задача имеет множество возможных решений, необходим критерий, позволяющий выбрать из этого множества наилучший вариант. Выбор наилучшего варианта математически обеспечивается отысканием экстремального значения некоторого экономического показателя, представленного в целевой функции, причем сама функция должна быть линейной.
г). Существенным требованием является условие неотрицательности переменных, поскольку искомые величины являются реальными положительными величинами.
2. Определение перечня переменных и ограничений. В постановке задачи должно быть четко определено, что является неизвестным, какие переменные величины и их численные значения необходимо найти в процессе решения.
Во-первых, перечень переменных величин должен отражать характер, основное содержание моделируемого экономического процесса.
Во-вторых, количество переменных зависит от выбора планового периода (долгосрочный, плановый, текущий), который оказывает существенное влияние на степень их детализации. Чем ближе период, тем больше детализация переменных.
В-третьих, количество переменных зависит от того, насколько подробно в модели должны быть представлены вид продукции, направление ее использования, способы и сроки производства и реализации продукции и т. д.
После установления состава переменных определяют систему ограничений модели, отражающих условия реализации задачи. Ограничения, представленные в виде линейных неравенств и уравнений, отражают организационно-экономические и технологические требования, которые характеризуют данное производство.
3. Сбор информации и разработка технико-экономических коэффициентов и констант. Источниками информации служат годовые отчеты, производственно-финансовые и перспективные планы, различные нормативные справочники.
Целью переработки исходной информации являются разработка и обоснование системы технико-экономических характеристик процесса или объекта. Для любой модели они формируются в виде технико-экономических коэффициентов 
, коэффициентов целевой функции 
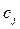и констант или объемных показателей ресурсов или продуктов 
.
4. Построение модели и ее математическая запись. Модель можно записать развернуто в виде системы неравенств и уравнений. Однако при достаточно большом числе переменных и ограничений такая запись громоздка, уменьшает обозримость и затрудняет чтение. Для более компактной записи используют общепринятую систему условных обозначений переменных величин, технико-экономических коэффициентов, констант и коэффициентов при переменных в целевой функции.
Для обозначения переменных величин наиболее употребительным символом является строчная или заглавная латинская буква х, X. Каждая конкретная переменная вводится в модель с соответствующим подстрочным индексом – порядковым номером – 1, 2, 3,..., п. Она обозначается 
, где п – порядковый номер последней переменной. Символ п показывает общее количество переменных в модели. Используя общий индекс j, необходимо указать, в каких пределах изменяются номера переменных. Например, вместо обозначения переменных с порядковыми номерами вводится 
(j = 1, 2, …, п), то есть j изменяется от 1 до п. Такая запись показывает, что в группу с индексом j входит п переменных.
Для обозначения правых частей ограничений (или констант) чаще всего используют строчную или заглавную латинскую букву В, b. Как правило, все константы имеют один индекс, показывающий принадлежность к конкретному ограничению. Например, 
. Для обозначения порядкового номера ограничения используют чаще всего индекс i. Количество ограничений обозначается буквой m (i = 1, 2,…, m).
Технико-экономические коэффициенты типа удельных затрат чаще всего обозначаются строчной латинской буквой , где i – номер ограничения, j – номер переменной. Коэффициенты пропорциональности, с помощью которых записывают соотношения между отдельными переменными величинами или их группами, чаще всего обозначаются символом 
.
Коэффициент при переменных в целевой функции чаще всего имеет один индекс, который показывает его принадлежность j -й переменной. Обозначается коэффициент целевой функции латинской строчной буквой с.
5. Перенесение информации на машинные носители, решение задачи на ЭВМ.
6. Анализ результатов решения, корректировка модели, повторное решение задачи на ЭВМ по скорректированной модели.
7. Экономический анализ различных вариантов и выбор проекта плана.
В конкретных условиях в зависимости от характера задачи последовательность этапов моделирования экономических процессов может меняться. [1]
1.2. Применение математического моделирования в сельском хозяйстве. Планирование оптимальной производственно-отраслевой структуры сельскохозяйственного предприятия
Объектами моделирования в сельскохозяйственном производстве являются: сельское хозяйство в целом как отрасль народного хозяйства, отдельные сельскохозяйственные отрасли, экономические районы и зоны, конкретные предприятия, а также отдельные подразделения предприятия и производственные процессы в них.
Экономические задачи характеризуются огромным количеством взаимосвязей, детальный учет которых приводит к очень громоздким и практически неиспользуемым моделям или системам моделей. Поэтому весьма важно включить в модель факторы, оказывающие основное влияние на производство, но не менее важно опустить те из них, которые играют второстепенную роль в данном процессе.
Отрасль сельского хозяйства можно рассматривать как вероятностную динамическую большую систему со своими входами и выходами. Она обменивается материальными, энергетическими и информационными потоками с внешней средой, состоящей из ряда общественных, технологических и природных систем.
Однако, сельское хозяйство, обладая всеми принципиальными чертами больших систем, имеет свои специфические особенности, значительно отличающие ее от технических больших систем. Оно, как отрасль общественного производства, развивается по общим экономическим законам, но отличается от других отраслей материального производства социально-экономической природой, средствами и условиями производства, производимой продукцией. Эти особенности сельскохозяйственного производства необходимо учитывать при математическом моделировании экономических процессов.
В сельском хозяйстве применение экономико-математических методов по сравнению с промышленностью имеет ряд дополнительных трудностей. Из-за многоотраслевого характера в сельском хозяйстве необходимо использовать большое количество переменных с очень сложной системой ограничений, в связи с чем модель имеет очень большую размерность, а их вычислительная реализация требует мощных ЭВМ. Часть количественных зависимостей в сельскохозяйственном производстве носит нелинейный характер и изменчивость параметров в больших пределах, что также затрудняет использование этих методов. Кроме того, в хозяйствах отсутствуют многие нормативные материалы, необходимые для применения экономико-математических методов. В то же время, по мнению многих экономистов, сельское хозяйство является наиболее перспективной отраслью для применения линейного программирования. Это объясняется, прежде всего, тем, что множество экономических задач оптимального использования ресурсов в сельском хозяйстве естественно вписывается в рамки моделей линейного программирования, т.к. основные допущения (линейность, суммируемость и др.), применяемые при построении моделей линейного программирования, в подавляющем большинстве случаев соответствуют объективно существующим связям сельскохозяйственного производства. Что же касается его специфических особенностей, таких как сезонность, строгая последовательность технологических процессов и т.п., то их можно учесть при разработке соответствующих линейных моделей.
Таким образом, для обеспечения оптимального функционирования отрасли необходимо основываться на тех же теоретических принципах, которые разрабатываются для оптимального функционирования экономики народного хозяйства в целом с учетом специфических особенностей развития сельского хозяйства. [2]
Теперь перейдем к планированию оптимальной производственно-отраслевой структуры сельскохозяйственного предприятия.
Постановка экономико-математической задачи оптимизации производственно-отраслевой структуры сельскохозяйственного предприятия. Требуется определить оптимально-производственную структуру, план использования ресурсов.
Для разработки модели необходимо знать:
1. специализацию хозяйства;
2. источники пополнения ресурсов и те их виды, объемы которых определяются в процессе решения задачи; основными ограничивающими ресурсами являются земельные и трудовые; некоторые виды ресурсов производятся в самом хозяйстве и потребляются в процессе производства (корма, органические удобрения);
3. источники удовлетворения потребности животных в кормах; виды животных, для которых предусматривается оптимизация кормовых рационов;
4. виды продукции, по которым устанавливаются объемы реализации на рынке, внутрихозяйственных потребностей;
5. размеры отраслей, которые следует ограничить.
Чтобы правильно поставить задачу необходимо изучить объект моделирования. Для этого нужно проанализировать уровень развития производства.
В качестве критерия оптимальности при оптимизации производственно-отраслевой структуры сельскохозяйственного предприятия могут использоваться следующие показатели:
· максимизируемые (при заданных объемах производственных ресурсов) – валовая продукция, товарная продукция, валовой доход, чистый доход, прибыль, уровень рентабельности;
· минимизируемые (при заданных объемах производства продукции) – материально-денежные затраты, затраты живого или совокупного труда и другие.
Состав переменных. Основные переменные данной модели отражают состав и размеры отраслей и видов деятельности предприятия с дифференциацией по направлениям использования продукции, степени интенсивности и трудоемкости производства, срокам реализации и другим признакам.
Помимо основных в модель могут вводиться вспомогательные переменные с целью оптимизации кормовых рационов, определения дополнительно привлекаемых ресурсов, а также объемов некоторых ресурсов, стоимостных показателей.
Экономико-математическая модель. Составить оптимальный план, то есть набор значений переменных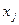 
, при котором достигается максимум выручки:
, (1.1)
где j – индекс вида деятельности растениеводства или животноводства; 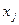– размер j- го вида деятельности растениеводства или животноводства (посевная площадь j- й культуры или поголовье j- говида животных; cej – цена продукции е -го вида в расчете на единицу j -го вида деятельности растениеводства или животноводства; е – индекс вида товарной продукции; 
– подмножество видов деятельности растениеводства и животноводства, продукция которых имеет товарное назначение; Е – множество видов товарной продукции.
Максимум целевой функции должен достигаться при выполнении следующих ограничений:
1) По земельным ресурсам. При разработке перспективного плана определяют размер, состав и качество земельных угодий. В модель вводят ограничения по пашне, естественным сенокосам и пастбищам. Если в хозяйстве имеются или проектируются улучшенные сенокосы и культурные пастбища, они учитываются отдельными ограничениями.
Математическая запись условий:
, (1.2)
где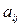 
– потребность в 
-м виде занимаемых угодий в расчете на единицу 
-го вида растениеводства;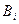 
– объем ресурса 
-го вида (в данном случае площади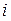 
-го вида земельных угодий); N – множество видов деятельности растениеводства; 
– множество видов земельных угодий.
2) По трудовым ресурсам. Количество трудовых ресурсов не должно превышать используемое количество трудовых ресурсов на предприятии.
, (1.3)
где t – индекс периода использования трудовых ресурсов (год, месяц, декада); Т – множество периодов; 
– норма затрат труда в расчете на единицу j -го вида деятельности в t -м периоде; Вit – наличие трудовых ресурсов в t-м периоде.
3) По кормовым ресурсам. Произведенные корма должны балансироваться с потребностью в них животноводства по кормовым единицам, а также выдерживать соотношение по группам кормов в соответствии с физиологическими потребностями животных.
, (1.4)
где l – индекс питательных веществ; L – множество питательных веществ; 
– выход питательных веществ l -го вида в расчете на единицу j -го вида деятельности растениеводства (на 1 га j -й культуры); 
– годовая нормативная потребность в l -м виде питательных веществ в расчете на одну среднегодовую голову j -го вида; N – множество видов деятельности растениеводства; D – множество видов деятельности животноводства.
4) По реализации продукции. Объем произведенной продукции должен удовлетворять условия договоров по продаже этой продукции.
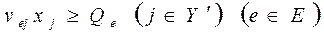, (1.5)
где vej – выход товарной продукции е -го вида в расчете на единицу j -го вида деятельности растениеводства или животноводства; е – индекс вида товарной продукции; Qe – объем реализации продукции е -го вида, прогнозируемый либо принимаемый в соответствии с заключенными договорами поставки (в соответствующих единицах измерения); – подмножество видов деятельности растениеводства и животноводства, продукция которых имеет товарное назначение; Е – множество видов товарной продукции.
5) Условие неотрицательности переменных:
. (1.6)
2. Характеристика Ордена Трудового Красного Знамени племзавод-колхоза имени 50-летия
Ордена Трудового Красного Знамени племзавод-колхоз имени 50-летия СССР – одно из наиболее крупных хозяйств Вологодской Области. Оно было образовано в 1960 году на базе четырех экономически слабых хозяйств.
Общая земельная площадь хозяйства составляет 12101 га, из них сельскохозяйственных угодий – 5162 га, в т. ч. пашни – 3653 га. Общее поголовье КРС – 3300 голов, в том числе коров – 1370. Имеется так же 58 тракторов, 26 грузовых машин, три автобуса и легковые автомобили. Численность работающих – 350 человек.
Колхоз специализируется на молочном животноводстве, откорме КРС и выращивании племенного скота черно-пестрой породы, семеноводстве зерновых и многолетних трав.
О размерах производства можно судить по таблице 2.1.
Таблица 2.1
Размеры производства Ордена Трудового Красного Знамени племзавод-колхоза имени 50-летия СССР
| Показатели | Отклонение | |||
| 2008 г. к 2009 г., ± | 2008 г. к 2009 г., % | |||
| Прибыль, тыс. руб. | 117,85 | |||
| Стоимость основных производственных фондов, тыс. руб. | 94554,5 | 101316,5 | 107,15 | |
| Среднесписочная численность работников, чел. | 101,45 | |||
| Производительность труда, руб | 114,25 |
Из таблицы видно, что рассматриваемый колхоз имеет средние размеры производства.
За рассматриваемый период (с 2008 по 2009гг) прибыль возросла на 17,85%, стоимость основных производственных фондов – на 7,15%, производительность труда – на 14,25%, среднесписочная численность персонала – на 1,45%.
В таблицах 2.2, 2.3 приведены натуральные объемы производства, данные о реализации продукции.
Таблица 2.2
Номенклатура и объем производства продукции в 2008-2009 гг., тонн
| Наименование показателей | Абсолютное отклонение | Темп роста | ||
| Зерно | 116,79% | |||
| Силос | 162,61% | |||
| Мука | -58 | 89,86% | ||
| Сено | -326 | 83,88% | ||
| Молоко | 115,81% |
Таблица 2.3
Реализация продукции в Ордена Трудового Красного Знамени племзавод-колхозе имени 50-летия СССР в 2008-2009 гг.
| Номенклатура | Реализовано продукции, ц | Цена, руб. | Выручено, тыс. руб. | |||
| 2008 г | 2009 г | 2008 г | 2009 г | 2008 г | 2009 г | |
| Молоко | ||||||
| Зерно | ||||||
| КРС в живой массе | ||||||
| Всего: |
Основную долю реализуемой продукции составляет молоко. Оно составляет около 80% от общей выручки.
Площадь сельскохозяйственных угодий в данном колхозе составляет 5159 га, из них 3652 га пашни. Пахотные угодия представлены дерново-, слабо-, средне-, сильно-подзолистыми почвами. Основными культурами, выращиваемыми в хозяйстве, являются яровой ячмень, овес, пшеница, многолетние травы.
Для сортообновления колхоз закупает семена элиты и суперэлиты.
Основными задачами, стоящими перед отраслью растениеводства, являются: сохранение плодородия почвы и обеспечение поголовье скота качественным кормом. Последнее – особенно важно, т.к. в связи с увеличением продуктивности дойного стада, и возросшими требованиями к качеству молока, возрастают и требования к качеству заготовляемых кормов.
Ведущей отраслью хозяйства является животноводство. Скот размещен в 15 типовых животноводческих помещениях с привязным и беспривязным способом содержания. Маточное поголовье коров сосредоточено на двух фермах: «Савкино» и «Степурино». Валовое производство молока составило за 2009 год 9601 т, удой на корову – 7101 кг. Все произведенное молоко отправляется на ООО «Данон-индустрия» (г. Москва).
В колхозе происходит постоянное обновление оборудования ферм. Для повышения качества молока была произведена замена старого холодильного оборудования на танки для охлаждения и хранения молока с автоматом промывки шведской фирмы DeLaval. На дворах с привязным содержанием стали использовать новые доильные аппараты той же фирмы. Благодаря этим нововведениям, в 2008 году было продано 98% молока сортом Евростандарт, средний процент жира в этом молоке составил 3,76%.
С 2004 года в колхозе был запущен в эксплуатацию двор беспривязного содержания коров с доильным залом. Преимущество беспривязного содержания молочного стада состоит в увеличении производительности труда, но, вместе с этим, требует более высокого уровня зоотехнической и селекционной работы, и соответственно, более квалифицированного персонала.
Рассмотрим существующую производственную программу изучаемого колхоза:
В хозяйстве имеется 4052 головы крупного рогатого скота, в том числе из них 1500 головы коров молочного направления.
Данные о землепользовании изучаемого колхоза представлены в таблице 2.4
Таблица 2.4
Фактическое использование земельных угодий колхоза
| Наименование культуры | Площадь, га |
| Озимые зерновые | |
| Яровые товарные | |
| Яровые фуражные | |
| Зернобобовые | |
| Кукуруза на силос и зеленый корм | |
| Силосные | |
| Многолетние травы на сено | |
| Многолетние травы на зеленый корм | |
| Естественные сенокосы | |
| Естественные пастбища |
Из таблицы 2.4 видно, что всех больше гектаров используется под яровыми фуражными и под многолетними травами, а всех меньше – под кукурузой и озимыми зерновыми.
Произведенные корма должны балансироваться с потребностью в них животноводства по кормовым единицам, а также выдерживать соотношение по группам кормов в соответствии с физиологическими потребностями животных. Проверим, выполняются ли зоотехнические требования в годовом рационе для стада коров молочного направления. Результаты представим в таблице 2.5.
Таблица 2.5
Эффективность фактического рациона кормления племзавода-колхоза имени 50-летия СССР
| Ограничения | Необходимая норма | Значение |
| Кормовых единиц, не менее, кг | 15,1 | 15,4 |
| Сухого вещества, не менее, кг | 18,9 | 16,8 |
| Перевариваемого протеина, г |
Рацион, который существует в хозяйстве, удовлетворяет не всем требованиям по содержанию питательных веществ.
Таким образом, существующую производственную структуру нельзя назвать оптимальной. Поэтому необходимо составить такую производственно-отраслевую структуру, которая будет давать колхозу наибольшую выручку и удовлетворять всем зоотехническим нормам.
Оптимизация производственно-отраслевой структуры племзавод-колхоза Имени 50-летия СССР
3 .1. Разработка числовой экономико-математической модели
Составим экономико-математическую модель поставленной задачи.
Постановка задачи. Определить оптимальную годовую производственно-отраслевую структуру племзавод-колхоза Имени 50-летия СССР Грязовецкого района, которая позволила бы получать максимальную выручку при следующих производственных условиях: ограниченность земельных и трудовых ресурсов, растениеводство обеспечивает кормами собственные производства в соответствии с зоотехническими нормами, размеры товарных отраслей должны удовлетворять условия договоров по продаже соответствующей продукции.
Критерий оптимальности: максимизировать выручку рассматриваемого колхоза.
Система переменных:
– площадь яровых зерновых товарных, га;
– площадь яровых зерновых фуражных, га;
– площадь озимых зерновых фуражных, га;
– площадь зернобобовых. га;
– площадь кукурузы на силос и зеленый корм, га;
– площадь силосных, га;
– площадь многолетних трав на сено, га;
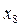– площадь многолетних трав на зеленый корм, га;
– площадь естественных сенокосов, га;
– площадь естественных пастбищ, га;
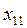– основное дойное стадо, гол.;
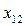– животные на выращивании и откорме, гол.
Система ограничений.
· Ограничения на производственные ресурсы;
· Ограничения по кормовой базе;
· Ограничения по реализации товарной продукции.
Исходные данные для модели:
В хозяйстве имеется 3757 га пашни, 399 га естественных сенокосов, 643 га естественных пастбищ. Необходимые данные по объемам товарной продукции и ценам ее реализации в отчетном году, растениеводству, животноводству представлены в таблицах 3.1, 3.2, 3.3, 3.4.
Таблица 3.1
Объем и цены реализации продукции
| Наименование продукции | Объем реализации, кг | Цены реализации 1 кг, руб. коп. |
| Яровые | 4,07 | |
| Молоко | 11,23 | |
| КРС (в живой массе) | 48,88 |
Таблица 3.2
Данные по растениеводству
| Культуры, угодья | Питательная ценность, кг корм. ед. | Выход продукции с 1 га, кг | Затраты труда на 1 га, чел.-ч за год | Выход питательных веществ с 1 га, кг корм. ед. |
| Яровые товарные | - | 16,4 | - | |
| Яровые фуражные | 1,21 | |||
| Озимые фуражные | 0,18 | 11,7 | 856,8 | |
| Зернобобовые | 1,08 | 1,7 | ||
| Кукуруза на силос и зеленый корм | 0,15 | 16,6 | ||
| Силосные | 0,22 | 9,1 | ||
| Многолетние травы на сено | 0,49 | 4,5 | 1582,7 | |
| Многолетние травы на зеленый корм | 0,17 | 1,05 | ||
| Естественные сенокосы | 0,42 | 2,5 | ||
| Естественные пастбища | 0,17 | 1,5 | 2789,7 |
Таблица 3.3
Исходные данные по животноводству (на 1 среднедневную голову)
| Показатели | Основное стадо молочного направления | Животные на выращивании и откорме |
| Среднегодовое поголовье, гол. | ||
| Продуктивность в год для реализации, кг | 7030,6 | 243,4 |
| Потребность в к.ед., кг | ||
| Прямые затраты труда на 1 голову, чел.-ч | 106,7 | 25,4 |
Таблица 3.4
Допустимые границы содержания отдельных групп кормов в годовых рационах животных, кг корм. ед.
| Корма | Молочное стадо | Животные на выращивании и откорме | ||
| min | max | min | max | |
| Концентрированные | ||||
| Грубые | ||||
| силос | ||||
| Зеленые |
Высокобелковые корма (зернобобовые: горох+овес) могут составлять в концентрированных кормах не более 30% их питательности.
Числовая модель.
I. Блок ограничений по использованию производственных ресурсов:
1) Площадь пашни, не более, га:
2) Площадь естественных сенокосов, не более, га:
3) Площадь естественных пастбищ, не более, га:
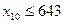
4) По использованию трудовых ресурсов, чел.-ч:
II. Блок ограничений по кормовой базе:
5) По кормовым единицам, кг:
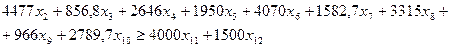
6) По концентрированным кормам – минимальное значение, кг корм. ед.:
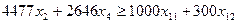
7) По концентрированным кормам – максимальное значение, кг корм. ед.:
8) По грубым кормам – минимальное значение, кг корм. ед.:
9) По грубым кормам – максимальное значение, кг корм. ед:
10) По силосу – минимальное значение, кг корм. ед.:
11) По силосу – максимальное значение, кг корм. ед.:
12) По зеленым кормам – минимальное значение, кг корм. ед.:
13) По зеленым кормам – максимальное значение, кг корм. ед.:
14) По общему весу зернобобовых в концентратах, кг корм. ед.:
III. Блок ограничений по выполнению условий договоров на продажу продукции, кг:
15) По реализации яровых зерновых, кг:
16) По реализации молока, кг:
17) По реализации крупного рогатого скота (в живой массе), кг:
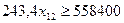
Количество гектаров посеянных культур и количество голов скота не может быть отрицательным, поэтому введем условие неотрицательности переменных:
Выручка должна быть максимальной. Составим целевую функцию, где коэффициентами при переменных выступает произведение цены реализации продукции на выход продукции:
Преобразуем функцию:
Таким образом, получим следующую числовую модель задачи:
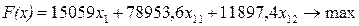(3,1)
(3,3)
Составленную модель решим, используя надстройку Поиск решения в Microsoft Excel. Получен следующий оптимальный план:
Площади, га:
=1900, =454,6, =0, =329,7, =0, =436,7, =517,9, 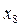=318,2, =399, =639,1;
Поголовье крупного рогатого скота, голов:
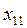=1361, 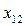=2295.
При этом максимальная выручка составляет 163369174,6 рублей.
