И методики измерений
Тангенс-гальванометр представляет собой плоскую вертикальную катушку радиуса R с некоторым числом витков N, в центре которой в горизонтальной плоскости расположена короткая магнитная стрелка (компас). Конец стрелки может перемещаться по шкале, разделённой на градусы. Магнитная стрелка при отсутствии тока в катушке будет расположена по магнитному меридиану Земли. Поворотом вокруг вертикальной оси можно добиться совмещения плоскости катушки с плоскостью магнитного меридиана; в этом случае стрелка компаса находится в плоскости катушки. После такой установки катушки пропускают по ней ток, в результате чего магнитная стрелка повернётся на некоторый угол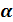 
. Объясняется это тем, что на магнитную стрелку будут действовать два поля: горизонтальная составляющая магнитного поля Земли 
и поле 
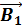, созданное током. Под действием этих полей магнитная стрелка займёт такое положение равновесия, при котором равнодействующая 
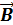двух полей будет совпадать с линией, полюса магнитной стрелки ns.
NS – направление магнитного меридиана земли; а и б – сечения витка катушки горизонтальной плоскостью; ns – магнитная стрелка, помещённая в центре катушки; – вектор горизонтальной составляющей индукции поля Земли; 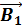– вектор индукции магнитного поля, созданного током.
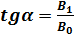, следовательно,
. (1)
Величина индукции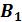 
поля. Созданного током в центре катушки, рассчитывается по закону Био – Савара – Лапласа:
,
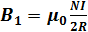где I – сила тока, текущего в витке; R – радиус витка; N – число витков;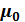 
– магнитная постоянная, равная 
.
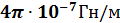Подставляя 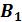в формулу (1) получим
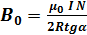, (2)
Этой формулой пользуются для опытного определения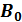 
. Кроме того, из выражения (2) можно получить
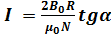. (3)
Анализ формулы (3) показывает, что сила тока в катушке пропорциональна тангенсу угла отклонения магнитной стрелки от горизонтальной составляющей вектора индукции магнитного поля Земли. Таким образом, этот прибор может служить также для измерения силы тока. В формуле (3) множитель
является постоянным для данного прибора, его называют переводным множителем тангенс-гальванометра. Таким образом, формулу (3) можно переписать так:
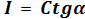. (4)
Отсюда следует, что постоянная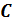 
численно равна тому току, который протекает по виткам, когда угол отклонения стрелки равен 
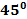. Для производства измерений пользуются схемой, где введены следующие обозначения: ТГ – тангенс-гальванометр, R – реостат, А – амперметр, П – переключатель.
Из выражений (3) и (4) получаем
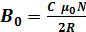. (5)
Порядок выполнения работы
1. Собрать цепь по схеме рис. 10.5 и установить плоскость катушки в плоскости магнитного меридиана Земли.
2. Включив полностью реостат R, присоединить собранную цепь к зажимам источника постоянного напряжения. Задать необходимую силу тока в катушке реостатом. Дождаться, когда магнитная стрелка придет в равновесие. Отсчитать углы α’1 и α’2 по обоим концам стрелки для уничтожения эксцентриситета стрелки (несовпадение оси стрелки с центром шкалы) и записать в таблицу наблюдения (табл. 10.1) уже средние из этих значений:
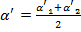. Измерить силу тока по амперметру А.
3. Не меняя силы тока, изменить его направление переключателем П и измерить величину α " опять по обоим концам стрелки. Переключение направления тока необходимо производить для уничтожения возможной ошибки из-за неточной установки плоскости катушки в плоскости магнитного меридиана.
4. Повторить опыт не менее 10 раз при различных силах тока. Сила тока может регулироваться изменением сопротивления реостата R.
5. Результаты измерений ипостоянные величины занести в таблицу (табл. 10.1).
Таблица 10.1
| Номер Измер. | I, A |  ,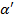
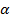град
|  ",
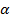град
| ,
град
| tg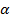
| N Вит. | R, см | µ0 Гн/м | B0, Тл | С, А |
6. Выписать ошибки прямых измерений и физических констант.
7. Построить график I=f (tgα).
8. По графику найти значение С и но формуле (5) вычислить Во.
Значение α берется равным среднему арифметическом α/1 и α/2:
