ЭЛЕКТРОСТАТИ́ЧЕСКОЕ ПО́ЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними.
Электростатическое поле характеризуется напряженностью электрического поля Е, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический заряд, помещенный в данную точку поля. Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.
Электростатическое поле однородно, если вектор его напряженности одинаков во всех точках поля, если вектор напряженности в различных точках различается, поле неоднородно. Одно из фундаментальных свойств электростатического поля заключается в том, что работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от траектории движения, а определяется только положением начальной и конечной точек и величиной заряда. Следовательно, работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Силовые поля, обладающие этим свойством, называют потенциальными или консервативными. То есть электростатическое поле - это потенциальное поле, энергетической характеристикой которого является электростатический потенциал, связанным с вектором напряженности Е соотношением:
Е = -gradj.
Для электростатических полей соблюдается принцип суперпозиции. Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов. Напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженности полей, создаваемых в данной точке каждым из зарядов в отдельности.
Всякий заряд в окружающем его пространстве создает электростатическое поле. Чтобы обнаружить поле в какой-либо точке, надо поместить в точку наблюдения точечный пробный заряд — заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле).
Поле, создаваемое уединенным точечным зарядом q, является сферически симметричным. Модуль напряженности уединенного точечного заряда в вакууме с помощью закона Кулона можно представить в виде:
Е = q/4peоr2.
Где eо — электрическая постоянная, = 8,85.10-12Ф/м.
Закон Кулона, установленный при помощи созданных им крутильных весов (см. Кулона весы), — один из основных законов, описывающих электростатическое поле. Он устанавливает зависимость между силой взаимодействия зарядов и расстоянием между ними: сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эту силу называют кулоновской, а поле — кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q < 0, то вектор направлен к заряду.
Электрическое поле можно характеризовать значением потока вектора напряженности электрического поля, который можно рассчитать в соответствии с теоремой Гаусса. Теорема Гаусса устанавливает связь между потоком напряженности электрического поля через замкнутую поверхность и зарядом внутри этой поверхности. Поток напряженности зависит от распределения поля по поверхности той или иной площади и пропорционален электрическому заряду внутри этой поверхности.
Если изолированный проводник поместить в электрическое поле, то на свободные заряды q в проводнике будет действовать сила. В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, компенсирует полностью внешнее поле, т. е. установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в ноль: во всех точках внутри проводника Е = 0, то есть поле отсутствует. Силовые линии электростатического поля вне проводника в непосредственной близости к его поверхности перпендикулярны поверхности. Если бы это было не так, то имелась бы составляющая напряженности поля, вдоль поверхности проводника и по поверхности протекал бы ток. Заряды располагаются только на поверхности проводника, при этом все точки поверхности проводника имеют одно и то же значение потенциала. Поверхность проводника является эквипотенциальной поверхностью. Если в проводнике есть полость, то электрическое поле в ней также равно нулю; на этом основана электростатическая защита электрических приборов.
Если в электростатическое поле поместить диэлектрик, то в нем происходит процесс поляризации — процесс ориентации диполей или появление под воздействием электрического поля ориентированных по полю диполей. В однородном диэлектрике электростатическое поле вследствие поляризации
23)Электрические токи в металлах
Природа электрического тока в металлах. Все металлы в твердом и жидком состоянии являются проводниками электрического тока. Специально поставленные опыты показали, что при прохождении электрического тока масса металлических проводников остается постоянной, не изменяется и их химический состав. На этом основании можно было предположить, что в создании электрического тока в металлах участвуют только электроны. Предположение об электронной природе электрического тока в металлах подтверждено опытами советских физиков Л. И. Мандельштама и Н. Д. Папалекси и американских физиков Т. Стюарта и Р. Толмена. В этих опытах было обнаружено, что при резкой остановке быстро вращающейея катушки в проводе катушки возникает электрический ток, создаваемый отрицательно заряженными частицами — электронами.
При отсутствии электрического поля свободные электроны перемещаются в кристалле металла хаотически. Под действием электрического поля свободные электроны, кроме хаотического движения, приобретают упорядоченное движение в одном направлении, и в проводнике возникает электрический ток. Свободные электроны сталкиваются с ионами кристаллической решетки, отдавая им при каждом столкновении кинетическую энергию, приобретенную при свободном пробеге под действием электрического поля. В результате упорядоченное движение электронов в металле можно рассматривать как равномерное движение с некоторой постоянной скоростью 
.
Так как кинетическая энергия электронов, приобретаемая под действием электрического поля, передается при столкновении ионами кристаллической решетки, то при прохождении постоянного тока проводник нагревается.
Зависимость удельного электрического сопротивления металлов от температуры. Удельное сопротивление металлов при нагревании увеличивается приблизительно по линейному закону (рис. 152):
, (44.1)
где 
— удельное электрическое сопротивление металла при температуре T, 
— его удельное сопротивление при 0 °С, 
— температурный коэффициент сопротивления, особый для каждого металла.
С приближением температуры к абсолютному нулю удельное сопротивление монокристаллов становится очень малым. Этот факт свидетельствует о том, что в идеальной кристаллической решетке металла электроны перемещаются под действием электрического поля, не взаимодействуя с ионами решетки. Длина их свободного пробега при этом может достигать значений порядка 1 см, т. е. в 107 - 108 раз превышает межатомные расстояния в кристалле. Электроны взаимодействуют лишь с ионами, не находящимися в узлах кристаллической решетки.
При повышении температуры возрастает число дефектов в кристаллической решетке из-за тепловых колебаний ионов,— это при водит к возрастанию удельного сопротивления кристалла.
Скорость упорядоченного движения электронов в проводнике. Для определения скорости упорядоченного движения свободных электрических зарядов в проводнике нужно знать концентрацию n свободных носителей заряда и силу тока I. Если концентрация свободных электрических зарядов в проводнике n, то за промежуток времени 
через поперечное сечение S проводника при скорости 
их упорядоченного движения проходит электрический заряд 
, равный
,
где e — модуль заряда электрона. Сила тока I в проводнике при том равна
.
Из последнего уравнения скорость упорядоченного движения электронов в проводнике получается равной
.
Концентрация свободных электронов в металлах примерно равна концентрации атомов, модуль заряда электрона e = 1,6 * 10-19 Кл. Для проводника с площадью поперечного сечения S = 1 мм2 = 10-6 м2 при силе тока I = 1 A скорость упорядоченного движения электронов равна
.
За 1 с электроны в проводнике перемещаются за счет упорядоченного движения меньше чем на 0,1 мм.
Малые значения скорости упорядоченного движения свободных зарядов в проводниках не приводят к запаздыванию зажигания электрических ламп, включения электромоторов и т. д., так как при включении электрической цепи вдоль проводов со скоростью света распространяется электромагнитное поле. Это поле приводит в движение свободные электрические заряды почти одновременно во всех проводниках электрической цепи.
29)Взаимодействие электромагнитных волн с веществом
Дисперсией света называется зависимость показателя преломления л вещества от частоты v (длины волны l) света или зависимость фазовой скорости v световых волн от его частоты v. Дисперсия света представляется в виде зависимости
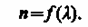
Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Первые экспериментальные наблюдения дисперсии света принадлежат И. Ньютону (1672 г.).
Рассмотрим дисперсию света в призме. Пусть монохроматический пучок света падает на призму с преломляющим углом А и показателем преломления п (рис. 268) под углом a1. После двукратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол j.
Предположим, что углы А и a1малы, тогда углы a2, b1и b2 будут также малы и вместо синусов этих углов можно воспользоваться их значениями. Поэтому a1/b1 = n, b2/a2 = 1/n, а так как b1 + b2 = A, то a2 = b2n = n(A - b1) = n(A - a1/n) = nA - a1, откуда
Из выражений (185.3) и (185.2) следует, что
(185.4)
т. е. угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы.
Из выражения (185.4) вытекает, что угол отклонения лучей призмой зависит от величины n - 1, а n - функция длины волны, поэтому лучи разных длин волн после прохождения призмы окажутся отклоненными на разные углы, т. е. пучок белого света за призмой разлагается в спектр, что и наблюдалось И. Ньютоном. Таким образом, с помощью призмы, так же как и с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав.
Рассмотрим различия в дифракционном и призматическом спектрах.
1. Дифракционная решетка разлагает падающий свет непосредственно по длинам волн (см. (180.3)), поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны. Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения длины волны света надо знать зависимость n = ¦(l) (185.1).
2. Составные цвета в дифракционном и призматическом спектрах располагаются различно. Из (180.3) следует, что в дифракционной решетке синус угла отклонения пропорционален длине волны. Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи в спектр по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны уменьшается (рис. 269). Поэтому красные лучи отклоняются призмой слабее, чем фиолетовые.
Величина
называемая дисперсией вещества, показывает, как быстро изменяется показатель прело мления с длиной волны. показатель преломления для прозрачных веществ с уменьшением длины волны увеличивается; следовательно, величина dn/dl по модулю также увеличивается с уменьшениемl.
Такая дисперсия называется нормальной. Как будет показано ниже, ход кривой n(l) - кривой дисперсии - вблизи линий и полос поглощения будет иным: nуменьшается с уменьшением l. Такой ход зависимости n от l называется аномальной дисперсией.
Блок
5)Фазовые переходы и экспериментальное исследование гистерезиса
Фа́зовый перехо́д (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий. С точки зрения движения системы по фазовой диаграмме при изменении её интенсивных параметров (температуры, давления и т. п.), фазовый переход происходит, когда система пересекает линию, разделяющую две фазы. Поскольку разные термодинамические фазы описываются различными уравнениями состояния, всегда можно найти величину, которая скачкообразно меняется при фазовом переходе.
Поскольку разделение на термодинамические фазы — более мелкая классификация состояний, чем разделение по агрегатным состояниям вещества, то далеко не каждый фазовый переход сопровождается сменой агрегатного состояния. Однако любая смена агрегатного состояния есть фазовый переход.
Наиболее часто рассматриваются фазовые переходы при изменении температуры, но при постоянном давлении (как правило равном 1 атмосфере). Именно поэтому часто употребляют термины «точка» (а не линия) фазового перехода, температура плавления и т. д. Разумеется, фазовый переход может происходить и при изменении давления, и при постоянных температуре и давлении, но и при изменении концентрации компонентов (например, появление кристалликов соли в растворе, который достиг насыщения).
Атомы тел обладают магнитным моментом. Под действием внешнего магнитного поля магнитные моменты атомов устанавливаются параллельно внешнему магнитномму полю. Таким образом, внутри тела создается дополнительное поле почти одинакового направления с внешним полем. Результатом сложения магнитных полей в теле является его магнитная индукция В. Она связана с индукцией внешнего намагничивающего поля В0 соотношением В=μ?В0, где μ – магнитная проницаемость среды, В0 – индукция намагничивающего поля.
В зависимости от величины μ все тела делятся на три класса: диамагнетики, парамагнетики и ферромагнетики. Для ферромагнетиков наблюдается явление гистерезиса, заключающееся в том, что магнитная индукция В зависит не только от индукции намагничивающего поля В0 в данный момент времени, но и от того какова индукция В была раньше.
Рассмотрим тороид, сердечником которого является ферромагнетик. При увеличении тока через обмотку тора, а, следовательно, и индукции внешнего намагничивающего поля В0, будет наблюдаться постепенное увеличение внутреннего поля тора В. Если ферромагнетик ранее не подвергался намагничиванию, то кривая зависимости В от В0 будет называться основной кривой намагничивания (отрезок ОВm рис.1).
Если, дойдя до точки Вm начать уменьшать намагничивающее поле В0, то индукция В будет уменьшаться по кривой ВmВост., т.е. с некоторым отставанием, носящим название гистерезиса.
Величина индукции, равная ОВост., называется остаточной индукцией и характеризует поле, которое остается в ферромагнетике при уменьшении внешнего поля до нуля.
При приложении поля, направленного противоположно первоначальному, будет происходить размагничивание ферромагнетика. Величина внешнего поля, при котором происходит полное размагничивание ферромагнетика, называется коэрцитивной силой (отрезок ОВок на рис.1).
Дальнейшее увеличение В вызывает намагничивание сердечника в противоположном первоначальному направлении, причем возрастание В будет идти в этом случае по кривой ВокВm. Уменьшая величину В до нуля, получим индукцию В, равную ОВост, которая называется отрицательной остаточной индукцией. Снова переменим направление тока и, увеличивая его, получим увеличение В0. Величина В0, равная Вок опять определяет коэрцитивную силу, необходимую для размагничивания ферромагнетика. При дальнейшем увеличении поля В0 будет происходить намагничивание ферромагнетика в первоначальном направлении, и петля гистерезиса замкнется в точке Внас., в которой ферромагнетик намагничен до насыщения.
Объяснить явление гистерезиса можно тем, что в ферромагнетиках имеются области - домены, в которых все атомы или молекулы без внешнего магнитного поля
намагничены до насыщения. Таких областей в теле много. Каждая из областей имеет свое направление магнитного поля, и в целом тело не намагничено.
При наложении внешнего магнитного поля эти области ориентируются вдоль него. При прекращении же действия внешнего поля не все области самопроизвольного намагничивания дезориентируются, так как изменить ориентировку группы молекул гораздо труднее, чем ориентировку отдельной молекулы. Для того чтобы тело стало ненамагниченным, надо наложить внешнее поле, обратное по знаку полю намагничивающему (коэрцитивная сила).
Петлю гистерезиса можно получить на экране электронно-лучевой трубки осциллографа. Для этого ферромагнетик помещают в магнитное поле, создаваемое переменным током. На горизонтально-отклоняющие пластины трубки подают напряжение UХ пропорциональное ВО, а на вертикально-отклоняющие UY пропорциональное В.
Следует учесть, что магнитные свойства ферромагнетиков в переменных магнитных полях характеризуются значением динамической магнитной проницаемости μ – представляющей собой отношение амплитудного значения индукции к амплитудному значению индукции внешнего намагничивающего поля.
(1)
Площадь динамической петли гистерезиса несколько больше площади статической петли, так как она соответствует потерям на вихревые токи и магнитную вязкость. Величина потерь на один цикл перемагничивания численно равна площади петли гистерезиса.
(2)
где 
, а аХ, аY – масштабная единица изображения петли.
В качестве исследуемого ферромагнетика служит материал, из которого изготовлен тор Т, первичная обмотка которого питается через сопротивление R1 переменным током.
Масштаб изображения динамической петли гистерезиса определяется следующим образом.
В первичной цепи амперметр А показывает эффективные значения тока, пропорциональные его амплитудным значениям Im:
(3)
Очевидно, что мгновенному значению тока Iт соответствует максимальное значение индукции намагничивающего поля Вom. Поэтому с учетом уравнения (3), можно написать
(4)
Таким образом, подставляя в формулу (4) показания IЭФ амперметра и указанное на рабочем месте численное значение n1 можно вычислить численное значение Вom. При помощи миллиметровой бумаги можно найти длину отрезка ОВom на осциллограмме в миллиметрах и определить горизонтальный масштаб изображения петли по формуле:
(5)
Аналогично можно определить вертикальный масштаб. Действительно, показания вольтметра V соответствуют эффективному значению напряжения:
(6)
где Um – амплитудное значение напряжения во вторичной обмотке, соответствующее максимальному значению Вm индукции В, отсюда
(7)
Зная показания UЭФ вольтметра и воспользовавшись данными, указанными на рабочем столе, можно найти численное значение Вm. При помощи миллиметровой бумаги можно найти длину отрезка ОВ = LВm в мм на осциллограмме и вычислить вертикальный масштаб по формуле
