Принцип суперпозиции электрических

Электричество и магнетизм

ЛЕКЦИЯ 11

ЭЛЕКТРОСТАТИКА

Электрический заряд

Большое количество явлений в природе связано с проявлением особого свойства эле-ментарных частиц вещества - наличия у них электриче­ского заряда. Эти явления были названы электрическими и магнитными.

Слово «электричество» происходит от греческого hlectron - электрон (янтарь). Способность натертого янтаря приобретать заряд и притягивать легкие предметы была отмечена еще в древней Греции.

Слово «магнетизм» происходит от названия города Магнезия в Малой Азии, вблизи которого были открыты свойства железной руды (магнитного железняка FеО∙Fе₂О₃) притягивать железные предметы и сообщать им маг­нитные свойства.

Учение об электричестве и магнетизме распадается на разделы:

а) учение о неподвижных зарядах и свя-занных с ними неизменных электрических полях - электростатика;

б) учение о равномерно движущихся заря-дах – постоянный ток и маг­нетизм;

в) учение о неравномерно движущихся зарядах и создаваемых при этом переменных полях - переменный ток и электродинамика, или теория элект­ромагнитного поля.

Электризация трением

Стеклянная палочка, натертая кожей, или эбонитовая палочка, натер­тая шерстью, при-обретают при этом электрический заряд или, как говорят, электризуются.

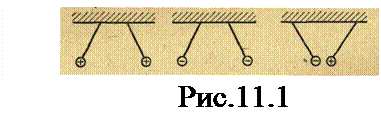Бузиновые шарики (рис.11.1), к которым прикоснулись стек-лянной па­лочкой, отталкиваются. Если к ним прикоснуться эбонитовой палочкой, они также отталки-ваются. Если же к одному из них прикоснуться эбонито­вой, а к другому стеклянной палочкой, то они притянутся.

Следовательно, существуют два типа электрических зарядов. Заряды, возникающие на потертом кожей стекле, условились назы-вать положи­тельными (+). Заряды, возникаю-щие на потертом шерстью эбоните, услови-лись называть отрицательными (-).

Опыты показывают, что одноименные заряды (+ и +, либо – и -) отталкиваются, разноименные (+ и -) притягиваются.

Точечным зарядом называется заряжен-ное тело, размерами которого можно прене-бречь по сравнению с расстояниями, на которых рас­сматривается воздействие этого заряда на другие заряды. Точечный заряд является абстракцией подобно материальной точке в механике.

Закон взаимодействия точечных

Зарядов (закон Кулона)

В 1785 г. французский ученый Огюст Кулон (1736—1806) на основании опытов с крутильными весами, на конце коромысла ко-торых помещались заряженные тела, а затем к ним подносились другие заряженные тела, уста­новил закон, определяющий силу взаимо-действия двух неподвижных точеч­ных зарядов Q ₁и Q ₂,расстояние между которыми r.

Закон Кулона в вакууме гласит: сила взаимодействия F между двумя неподвиж-ными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q ₁и Q ₂и обратно пропорциональна квадрату расстоя-ния r между ними:

,

где коэффициент k зависит от выбора системы единиц и свойств среды, в которой осу­ществляется взаимодействие зарядов.

Величина, показывающая, во сколько раз сила взаимодействия между зарядами в данном диэлектрике меньше силы взаимодействия между ними в вакууме, называется относительной диэлектрической проницаемостью среды e.

Закон Кулона для взаимодействия в среде: сила взаимодействия между двумя точечными зарядами Q ₁и Q ₂ прямо пропор-циональна произведению их величин и обрат-но пропорциональна произведению диэлек-трической про­ницаемости среды e _. на квадрат расстояния r между зарядами:

.

В системе СИ , где e₀ –диэлект-рическая проницаемость ва­куума, или элект-рическая постоянная. Величина e ₀ относится к числу фундамен­тальных физических пос-тоянных и равна e ₀=8,85∙10^-12 Кл²/(Н∙м²), или e ₀=8,85∙10^-12 Ф/м, где фарад (Ф) - единица электрической емкости. Тогда .

С учетом k закон Кулона запишется в окончательном виде:

,

где ee ₀= e _а - абсолютная диэлектрическая прони­цаемость среды.

Закон Кулона в векторной форме.

,

где F ₁₂ - сила, действующая на заряд Q ₁со стороны заряда Q ₂, r ₁₂- радиус-вектор, соединяющий заряд Q₂ с зарядом Q _1, r =|r₁₂| (рис.11.1).

 

На заряд Q ₂со стороны заряда Q ₁действует сила F ₂₁ =- F ₁₂, т.е. справедлив 3-й закон Ньютона.

11.4. Закон сохранения электрического

Заряда

Из обобщения опытных данных был установлен фундаментальный закон природы, экспериментально подтвержденный в 1843 г. английским физиком Майклом Фарадеем (1791—1867), - закон сохранения заряда.

Закон гласит: алгебраическая сумма электрических зарядов любой замкнутой сис-темы (системы, не обменивающейся зарядами с внешними тела­ми) остается неизменной, какие бы процессы ни происходили внутри этой системы:

.

Закон сохранения электрического заряда выполняется строго как в мак­роскопических взаимодействиях, например при электри-зации тел трением, когда оба тела заряжаются численно равными зарядами противополож-ных знаков, так и в микроскопических взаимодействиях, в ядерных реакциях.

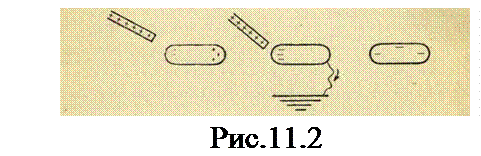Электризация тела через влияние (электростатическая индукция). При поднесении к изолированному проводнику заряженного тела происхо­дит разделение зарядов на проводнике (рис. 79).

 

 

Если индуцированный на удаленном конце проводника заряд отвести в землю, а затем, сняв предварительно заземление, убрать заряженное тело, то оставшийся на проводнике заряд распределится по провод-нику.

Опытным путем (1910—1914) американс-кий физик Р. Милликен (1868—1953) пока­зал, что электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е (е =1,6∙10^-19 Кл). Электрон (т_е= 9,11∙10^-31 кг) и протон (m_p =1,67∙10^-27 кг) являются соответст-венно носителями элементарных отрицатель-ного и положительного зарядов.

Электростатическое поле.

Напряженность

Неподвижный заряд Q неразрывно свя-зан с электрическим полем в ок­ружающем его пространстве. Электрическое поле представляет собой особый вид материи и является материальным носителем взаимо-дей­ствия между зарядами даже в случае отсутствия вещества между ними.

Электрическое поле заряда Q действует с силой F на помещаемый в ка­кую-либо из точек поля пробный заряд Q ₀.

Напряженность электрического поля. Вектор напряженности электрического поля в данной точке - физическая величина, определяемая силой, действующей на проб-ный единичный положительный заряд, поме-щенный в эту точку поля:

.

Напряженность поля точечного заряда в вакууме

.

Направление вектора Е совпадает с напра-влением силы, действующей на положитель­ный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положи­тельного заря-да); если поле создается отрицательным заря-дом, то вектор Е направлен к заряду (рис. 11.3).

Единица напряжен-ности электрического по­ля — ньютон на кулон (Н/Кл): 1 Н/Кл – напря-женность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл=1 В/м, где В (вольт) — еди­ница потенциала электростатического поля.

Линии напряженности.

Линии, касательные к которым в каждой их точке совпадают по направлению с вектором напряженности в этой точке, называ­ются линиями напряженности (рис.11.4).

Напряженность поля точечного заряда q на расстоянии r от него в системе СИ:

.

Линии напряженности поля точечного заряда представляют собой лучи, выходящие из точки, где помещен заряд (для положите-льного заряда), или входящие в нее (для отрицательного заряда) (рис.11.5,а, б ).

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились про­водить их с определенной густотой (см. рис.11.4): число линий напряженности, прони­зывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизыва­ющих элементарную площадку d S, нормаль n кото-рой образует угол a с векто-ром Е, равно E d Scos a =E_n d S, где Е _n - проекция вектора Е на нормаль n к площадке d S (рис.11.6). Величина

называется потоком вектора напряжен-ности через площадку d S. Единица потока вектора напряженности электростатического поля — 1 В∙м.

Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверх­ность

, (11.5)

где интеграл берется по замкнутой поверх-ности S. Поток вектора Е является алгебра­и-ческой величиной: зависит не только от конфигурации поля Е, но и от выбора направления n.

Принцип суперпозиции электрических

Полей

Если электрическое поле создается заря-дами Q ₁, Q ₂, …, Q_n, то на пробный заряд Q ₀действует сила F равная векторной сумме сил F _i, приложенных к нему со стороны каждого из зарядов Q _i:

.

Вектор напряженности электрического поля системы зарядов равен геометрической сумме напряженностей полей, создаваемых каждым из заря­дов в отдельности:

.

Эта принцип суперпозиции (наложения) электростатических полей.

Принцип гласит: напряженность Е результирующего поля, создаваемого систе-мой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчи-тать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Поле диполя. Принцип суперпозиции применим для расчета электростатического поля элект­рического диполя.

Электрический диполь - система двух равных по модулю разноименных точечных зарядов (+ Q, -Q),расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя l. Вектор

,

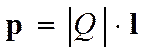совпадающий по направлению с плечом ди-поля и равный произведению заряда на плечо l, называется электрическим момен-том диполя или дипольным моментом (рис.11.7).

 

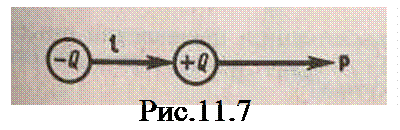
Согласно принципу суперпозиции полей, напряженность Е поля диполя в произ­вольной точке

Е = Е ₊+ Е _- ,

где Е₊ и Е_- - напряженности полей, создавае-мых соответственно положительным и отри-цательным зарядами.

Воспользовавшись этой формулой, рассчитаем напряжен­ность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.

1. Напряженность поля на продолжении оси диполя в точке А (рис.11.7).

Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна

Е_А = Е ₊- Е _- .

Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы (11.2) для вакуума можно записать

.

Согласно определению диполя, l /2<< r, поэтому

.

2. Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке В (рис.11.7). Точка В равноудалена от зарядов, поэтому

,

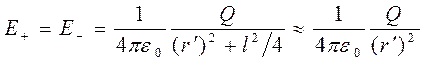где r' — расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, опирающихся на плечо диполя и вектор Е_В получим

,

откуда .

Подставив в последнее выражение значение Е₊, получим

.

Вектор Е _В имеет направление, противоположное вектору электрического момента диполя (вектор р направлен от отрицательного заряда к положительному).